ピタゴラスは、張った弦の2/3のポイントを押さえれば、
元の音と気持ちよく響くことを発見します。
それが数学的な見方からのハーモニーの発見であり、
五度、つまり、C(ド)に対してならば、G(ソ)の音になります。
ならば、G(ソ)の音を元にすれば、その五度上の音、
つまり、D(レ)という気持ち良い響きの音が得られます。
同じようにして、それを積み上げて行けば、
12回目で元のC(ド)の音に戻ってきます。
時計の数字や干支が12であるように、
音楽の音もまた不思議と12で和を閉じ、
五度圏ができあがります(図参照)。
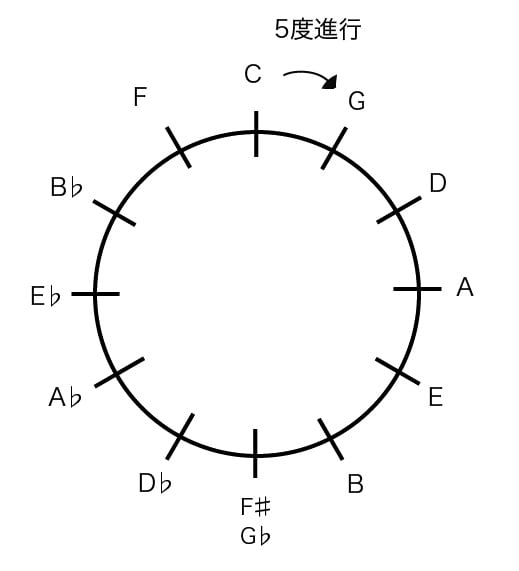
ところが、一周回って戻ってきたC(ド)の音は、
元のC(ド)の音とズレができます。
この差を「ピタゴラスコンマ」といい、
この微妙な音の差をなんとかするためにできたのが「平均律」。
一般の人にとっては、どうでもいいやん、という微妙な差ですが、
こだわる音楽家にとっては、殺人事件の動機にもなるぐらいのおおきな差なのです。
マイクロチューニング機能のあるキーボードで、「平均律」と「純正調」によって、
Cのコードとその半音上のD♭のコードを弾いてみました。聴き比べてみてください。
禅の思想によれば、完全なものは却って不完全である、といいます。
そういう意味でいえば、このピタゴラスコンマの不完全さが音楽をより深いものにしているのかもしれないですね。
※参考;日本では、中根元圭という和算家(数学者)が1700年ぐらいに十二平均律を考えていたそうです。これはすごい。
------------------------------------------------------------------------------
3/21(月・祝)ミュージックセンター御池 講師デモ演奏 at ゼスト御池 pm16:00 ~
小川敦子(Vocal) 光田英生(Guitar) 岩崎明(Keyboard)









