算数クイズ図形、いよいよ本番!早稲田(わせだ)大学の入試問題にチャレンジ!前回までをおさらいしておこう。小中学生にもとけますよ。
[問題]
半径(はんけい)r(あーる)の球(きゅう)の表面(ひょうめん)に、異(こと)なる四つの点A,B,C,Dがあります。AB=CD=2、AC^2=AD^2=BC^2=BD^2=6であるとき、r^2の長さをもとめなさい。※「^2」は2乗(にじょう)をあらわします。
球【きゅう】
ボールのような立体(りったい)。平面(へいめん)で切ると円(えん)ができる。円は「線対称」(せんたいしょう)なので、球も「線対称」になる。
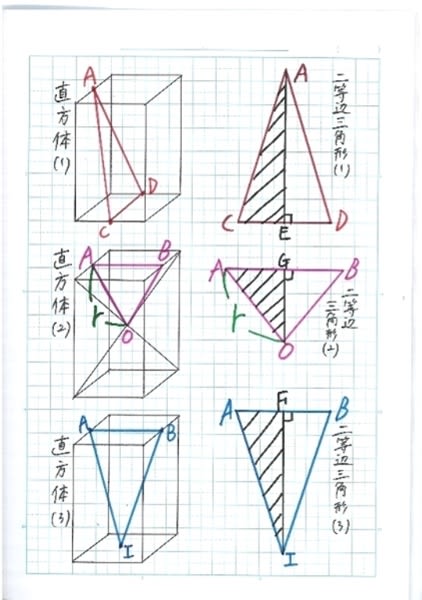
写真を見てください。直方体(1)に、二等辺三角形ACDをかきます。二等辺三角形ACDに「対称軸」(たいしょうじく)をひき、直角三角形ACEをつくります。斜線(しゃせん)をひいた図形です。これは直角三角形なので、「三平方の定理」(さんへいほうのていり)がなりたちます。
CE=EDで、CEはCDの半分なので、
CE=CD÷2=2÷2=1
また、[問題]より
AC^2=6
三平方の定理より
AC^2=CE^2+AE^2
6=1^2+AE^2
AE^2=6-1=5
AEは、直方体(3)のAIとおなじ
AE^2=AI^2=5
次に、直方体(2)に二等辺三角形ABOをかきます。ここでのO(オー)は、直方体の対角線(たいかくせん)の交点(こうてん)で、もとの球の中心になります。つまり、AOは球の半径rにもなります。
二等辺三角形ABOに「対称軸」をひき、直角三角形AGOをつくります。斜線をひいた図形です。これも直角三角形なので、「三平方の定理」がなりたちます。
AG=GBで、AGはABの半分なので、
AG=AB÷2=2÷2=1
三平方の定理より
AO^2=AG^2+OG^2(=r^2)
OG^2がわかればこの式が解けますね。
最後に、直方体(3)に二等辺三角形ABIをかきます。二等辺三角形ABIに「対称軸」をひき、直角三角形AFIをつくります。斜線をひいた図形です。これも直角三角形なので「三平方の定理」がなりたちます。
AF=FBで、AFはABの半分なので、
AF=AB÷2=2÷2=1
先に求めた
AE^2=AI^2=5
三平方の定理より
AI^2=AF^2+FI^2
5=1^2+FI^2
FI^2=5-1=4
FI^2=4=2×2
FI=2
OGはFIの半分ですから
OG=FI÷2=2÷2=1
OG^2=1×1=1
AO^2=AG^2+OG^2(=r^2)
r^2=1^2+1^2
r^2=1+1=2
大学の入試問題がとけました!(ZR)
[問題]
半径(はんけい)r(あーる)の球(きゅう)の表面(ひょうめん)に、異(こと)なる四つの点A,B,C,Dがあります。AB=CD=2、AC^2=AD^2=BC^2=BD^2=6であるとき、r^2の長さをもとめなさい。※「^2」は2乗(にじょう)をあらわします。
球【きゅう】
ボールのような立体(りったい)。平面(へいめん)で切ると円(えん)ができる。円は「線対称」(せんたいしょう)なので、球も「線対称」になる。
写真を見てください。直方体(1)に、二等辺三角形ACDをかきます。二等辺三角形ACDに「対称軸」(たいしょうじく)をひき、直角三角形ACEをつくります。斜線(しゃせん)をひいた図形です。これは直角三角形なので、「三平方の定理」(さんへいほうのていり)がなりたちます。
CE=EDで、CEはCDの半分なので、
CE=CD÷2=2÷2=1
また、[問題]より
AC^2=6
三平方の定理より
AC^2=CE^2+AE^2
6=1^2+AE^2
AE^2=6-1=5
AEは、直方体(3)のAIとおなじ
AE^2=AI^2=5
次に、直方体(2)に二等辺三角形ABOをかきます。ここでのO(オー)は、直方体の対角線(たいかくせん)の交点(こうてん)で、もとの球の中心になります。つまり、AOは球の半径rにもなります。
二等辺三角形ABOに「対称軸」をひき、直角三角形AGOをつくります。斜線をひいた図形です。これも直角三角形なので、「三平方の定理」がなりたちます。
AG=GBで、AGはABの半分なので、
AG=AB÷2=2÷2=1
三平方の定理より
AO^2=AG^2+OG^2(=r^2)
OG^2がわかればこの式が解けますね。
最後に、直方体(3)に二等辺三角形ABIをかきます。二等辺三角形ABIに「対称軸」をひき、直角三角形AFIをつくります。斜線をひいた図形です。これも直角三角形なので「三平方の定理」がなりたちます。
AF=FBで、AFはABの半分なので、
AF=AB÷2=2÷2=1
先に求めた
AE^2=AI^2=5
三平方の定理より
AI^2=AF^2+FI^2
5=1^2+FI^2
FI^2=5-1=4
FI^2=4=2×2
FI=2
OGはFIの半分ですから
OG=FI÷2=2÷2=1
OG^2=1×1=1
AO^2=AG^2+OG^2(=r^2)
r^2=1^2+1^2
r^2=1+1=2
大学の入試問題がとけました!(ZR)





















