今回は、私立(しりつ)中学の入試(にゅうし)問題です。平方(へいほう)をつかって、面積(めんせき)をもとめよう!
前回のおさらいです。「^2」は2乗(にじょう)をあらわします。「cm^2」は「平方センチメートル」とよみます。「2乗」と「平方」(へいほう)とはおなじものです。
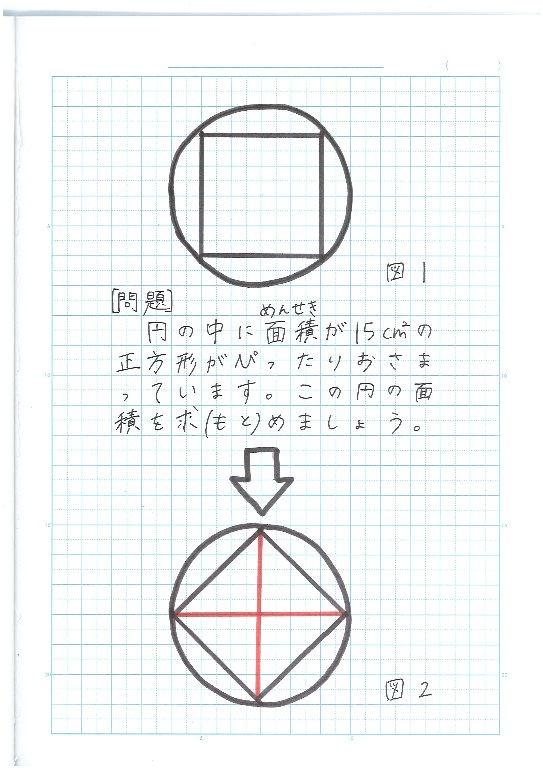
まず、写真の図1をみてください。円のなかに、面積が10cm^2の正方形がぴったりおさまっています。この円の面積をもとめましょう。
正方形の面積=一辺(いっぺん)×一辺です。この問題では、一辺×一辺=10cm^2 になりますが、算数ではこの一辺はだせません。でも答えはでます!
つぎは、写真の図2をみてください。これは、図1を90°回転(かいてん)させたものです。ひし形(がた)だ!正方形は、ひし形の一種(いっしゅ)です。ひし形の面積=対角線(たいかくせん)×対角線÷2 です。赤色の線が、このひし形の対角線です。
対角線×対角線÷2=10
対角線×対角線 =10×20
赤色の対角線は、この円の直径(ちょっけい)にもなってます。
対角線×対角線=20
直径×直径 =20
半径(はんけい)は、直径の半分です。
半径=直径÷2
半径×半径=20÷2÷2
半径×半径=5
円の面積= 半径×半径 ×3.14
=(半径×半径)×3.14
= 5 ×3.14
でました!計算をしてください。答えには単位(たんい)をつけるのをわすれずに。
半径×半径のように、おなじ数を2回かけることを「2乗」(にじょう)または「平方」(へいほう)とよびます。3の2乗は、3^2=3×3=9 です。
前回の「三平方(さんへいほう)の定理(ていり)」も、中学でならう「平方根」(へいほうこん)も、面積の単位の平方センチメートルも、2乗をつかいます。
面積の公式をおぼえておきましょう。
正方形の面積=一辺×一辺
ひし形の面積=対角線×対角線÷2
円の面積=半径×半径×3.14
続きます。(ZR)
前回のおさらいです。「^2」は2乗(にじょう)をあらわします。「cm^2」は「平方センチメートル」とよみます。「2乗」と「平方」(へいほう)とはおなじものです。
まず、写真の図1をみてください。円のなかに、面積が10cm^2の正方形がぴったりおさまっています。この円の面積をもとめましょう。
正方形の面積=一辺(いっぺん)×一辺です。この問題では、一辺×一辺=10cm^2 になりますが、算数ではこの一辺はだせません。でも答えはでます!
つぎは、写真の図2をみてください。これは、図1を90°回転(かいてん)させたものです。ひし形(がた)だ!正方形は、ひし形の一種(いっしゅ)です。ひし形の面積=対角線(たいかくせん)×対角線÷2 です。赤色の線が、このひし形の対角線です。
対角線×対角線÷2=10
対角線×対角線 =10×20
赤色の対角線は、この円の直径(ちょっけい)にもなってます。
対角線×対角線=20
直径×直径 =20
半径(はんけい)は、直径の半分です。
半径=直径÷2
半径×半径=20÷2÷2
半径×半径=5
円の面積= 半径×半径 ×3.14
=(半径×半径)×3.14
= 5 ×3.14
でました!計算をしてください。答えには単位(たんい)をつけるのをわすれずに。
半径×半径のように、おなじ数を2回かけることを「2乗」(にじょう)または「平方」(へいほう)とよびます。3の2乗は、3^2=3×3=9 です。
前回の「三平方(さんへいほう)の定理(ていり)」も、中学でならう「平方根」(へいほうこん)も、面積の単位の平方センチメートルも、2乗をつかいます。
面積の公式をおぼえておきましょう。
正方形の面積=一辺×一辺
ひし形の面積=対角線×対角線÷2
円の面積=半径×半径×3.14
続きます。(ZR)





















