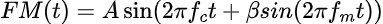FM音源

シンセサイザーの話をしよう。

「標準的な」シンセサイザーは次のような回路の「連結」によって構成されている。

OSCとはオシレータ(発振器)の事だ。ここがある音程での波形を創出する。キーボードのキーを弾くと、そのキーに見合った「波形」が鳴るわけだ。そして(この図だと3つだが)各オシレータが発声した波形はまずMIX(ミキサー)に送られ混ぜられる。

それがVCF(フィルタ)に送られる。フィルタは要はイコライザの仲間だ。ここでミックスされた各オシレータから送られてきた「合成波形」の倍音を削ったりする。そしてそれがVCA(アンプリファイア)に送られた後出力に送られる。アンプリファイアはそのまま「ボリューム調整」を行ってる。

EG(エンベロープ・ジェネレーター)とはフィルタやアンプリファイアのかかりを「時間的に調整する」ブツだ。徐々に倍音が削られたり、徐々にボリュームが大きくなったり、と言った「音色の演出」を司る。

このシステムは現在主流のデジタルシンセサイザーでもほぼ変わってない。フィルタで「倍音を削る」と言う事から翻って「倍音減算方式」なぞと呼ぶ。

元々、登場時のシンセサイザーは、オシレータ、フィルタ、アンプリファイア、エンベロープ・ジェネレーターはそれぞれ「ユニット」になっていて、それらを配線で繋いで音を出す機械だった。

このタイプのシンセサイザーは「接続による」音作りの自由度は極めて高かったんだけど、それでも実は「定型パターン」が存在してて、それが上で書いたオシレータ->フィルタ->アンプリファイアの流れだったんだ。

そのため、元々シンセサイザーは「スタジオ録音用機器」として考えられてたが、ライブ用として「良くあるパッチング」を固定された事で、今あるシンセサイザーの基礎の「流れ」が成立したわけだな。

ところで、元々シンセサイザーはアナログ機器であり、音も全部電気的に生成している・・・ザックリ言うと「交流電源」から流れてくる電流を上手く使って「音波」に変換してるわけだ。デジタルシンセみたいに「数学的な某を」演算して波形を生成してるわけじゃない。オシレータとはそういう「アナログ発振器」の事なんだ。

当然複雑な波形は生成出来ないんで、通常、アナログ・シンセサイザーは3つくらいの波形しか持っていない。それらは通常、三角波、ノコギリ波、矩形波、の3つだ。

三角波

ノコギリ波

矩形波

さて、ここで疑問に思う人もいるだろう。

「あれ、3つしか波形が無い、って事は結果的に3つの音色しか出ないんじゃない?」

と。

実はその通りなんだ(笑)。いくらフィルタやアンプリファイアで加工しようともオリジナルの波形がたった3つしかないと当然音色づくりには限界がある。

シンセサイザーが開発され売り出された時には「無限の音色の可能性」とか言われたけど、実はそんな事はない(笑)。結局3種類の波形を加工するだけの「三角波、ノコギリ波、矩形波を奏でる楽器だ」ってのがアナログ・シンセサイザーの本質的なトコで、それが往年の「シンセサイザーらしさ」だったんだな(※1)。

そして登場から20年くらい経つと結構飽きられてきたわけだ。

一方、じゃあ現代のデジタルシンセはどうなってるのか。

実は部品はデジタル化してるんだけど、回路構成、っつーか流れは全く往年のアナログ・シンセサイザーのまんま、なんだ。

しかし、変わったのが「オシレータ」部。ザックリ言うと、この「オシレータ」が発する音波が、かつての三角波、ノコギリ波、矩形波ではなく、実際にリアルにある楽器なんかを「サンプリング」(デジタル的に録音)したモノとなっている。そして3種類、なんじゃなくって、今だと最低でも500種類くらいは超えてるんじゃないか。

言わば、オシレータがCDみたいになっていて、キーを弾くと「実際に演奏された音」が鳴るようになってるわけだ。かつてのシンセは「現実にあり得ないような音を作る」楽器だったが、現代のデジタルシンセは「現実に存在する音をシミュレートする」楽器へと意味合いが変わってしまった。

言い換えると、実は現代のシンセはかなりの力技だ(笑)。1980年代には考えられなかったような半導体、要はROMの進歩で、大量のデジタルデータを抱えた「音色再生機」となってるんだ。

さて、シンセサイザーが登場してほぼ10年後の1970年代半ば。この頃になると「シンセサイザーをデジタル化しよう」とする研究が始まった。

一つのポイントとして、上に書いてきたような「アナログ・シンセサイザーの構造」がまずは疑問視されたわけ。

フィルタはそもそも「音を削る」為に存在する。仮に、オシレータが色んな波形を生み出せるのなら、フィルタに頼らなくてイイんじゃないか、って事だよな。

先ほど、現代のデジタルシンセは本体のROMに「現実にある楽器の音」等をしこたま詰め込んでる、と言う話をした。これはROMがコスパとしてはかなり良くなってきてて、大容量のデータを扱えるようになった、ってのが大きい。

一方、1970年代はまだまだそういう「メモリ用半導体」の値段が高かったわけだ。

従って「どうやってデジタル的に波形を即座に生成するんだ?」ってのが興味の対象になっていたわけ。

前回チラッと見たが、フランスにフーリエさんと言う人がいた。彼が数学的に「ジュテーム!」って言いながら発見したのは

「この世にある全ての音は、振幅・周波数・位相が違う様々なサイン波に分解出来る!」

と言う事だ。これをフーリエ解析、と呼ぶ。

逆に言うと、振幅・周波数・位相(これはまだ扱ってないが後に)が違うサイン波を足し合わせて行けば任意の音波を作り出せる、って事だ。これを倍音加算方式と呼ぶ。

最初のデジタルシンセサイザーの研究はこの倍音加算方式から始まった。

知る人ぞ知るマイナーなシンセサイザー、RMI Harmonic Synthesizer(1975年)。こんなナリだがれっきとしたデジタルシンセサイザーで、しかも初の商用化デジタルシンセサイザーだ。音源は倍音加算方式。ただし、フィルタも搭載している。

ところで、Scilabはなかなか面白い。

フツーのプログラミング言語は基本、文字列処理を目的とする。よくってグラフィクスを扱うぐらいだ。

せいぜいフツーのプログラミング言語の出力は、文字列、そして絵に限定される。

ところが、Scilabには「音声出力」と言う機能が備わってる。直接音声を計算して出力出来るわけで、「第3の出力方式を備えてる」と言うのはなかなかに強力な機能だと思う。

言っちゃえば、僕らはScilabを使う事で、「発振器」を手に入れた事になる。いや、ある意味これは「記述式のデジタルシンセサイザー」だと言う事だ。

ここではまずは、Scilabで「倍音加算」と言う方式の実験をしてみよう。

Scilabで次のようなスクリプトを書いてみる。

Fs = 44100;
duration = 10;
t = 0:1/Fs:duration;

function [w]=dampedoscillation(amp, rate, f, t)
　w = 2 ^ (amp/6) * exp(-rate * t) .* sin(2 * %pi * f * t)
endfunction

// 特徴の異なる正弦波を21個生成
w1 = dampedoscillation(-32, 0.85, 201, t);
w2 = dampedoscillation(-34.5, 0.8, 337, t);
w3 = dampedoscillation(-39.8, 1, 437, t);
w4 = dampedoscillation(-50.2, 1, 453, t);
w5 = dampedoscillation(-45.6, 1, 479, t);
w6 = dampedoscillation(-35.6, 1, 501, t);
w7 = dampedoscillation(-35.7, 1.25, 678, t);
w8 = dampedoscillation(-36.3, 1.5, 885, t);
w9 = dampedoscillation(-38.4, 1.5, 1093, t);
w10 = dampedoscillation(-45, 4, 1234, t);
w11 = dampedoscillation(-45, 3.5, 550, t);
w12 = dampedoscillation(-45, 4, 1401, t);
w13 = dampedoscillation(-45, 4, 1690, t);
w14 = dampedoscillation(-45, 4, 1780, t);
w15 = dampedoscillation(-45, 4, 2002, t);
w16 = dampedoscillation(-45, 4, 2449, t);
w17 = dampedoscillation(-45, 5, 2651, t);
w18 = dampedoscillation(-50, 3.5, 2889, t);
w19 = dampedoscillation(-50, 5, 3002, t);
w20 = dampedoscillation(-50, 6, 3250, t);
w21 = dampedoscillation(-50, 6, 3700, t);

// 波形を合成
w = w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 + w9 + w10 + w11 + w12 + w13 + w14 + w15 + w16 + w17 + w18 + w19 + w20 + w21;

ここで新しく出てくる数学は減衰振動、の記述式だ。確かにこれは大学時で習う数式だが、材料は高校数学で習っている。また、前回のサイン波の応用でもある(※2)。

単純には指数関数と三角関数の組み合わせ、だ。

波形w1の概形。振動の形成自体はそのままサイン波だが、最大値と最小値がどんどん減っていく。これが掛け合わされた指数関数の効果で、結果、時間が経る毎に音量が小さくなっていく。

要は、定義された関数dampedoscillationは、数学的には次の式を表している。

振幅が2の6分のamp乗になって、λ = -rateになってる、と式の基礎的なトコが置き換わってるだけ、なのが分かるだろう。

なお、Scilabの計算の基本は行列演算に基づいてるので、ベクトルの要素と別のベクトルの要素を順次単に掛け合わせたい、と言った場合、*と言う演算子の代わりに.*と言う演算子を用いる。

要は、tがベクトルな以上、exp(-rate × t)はベクトルとなり、sin(2πft)もベクトルになるんで、上のwの計算式を成り立たせる為には.*を使わないとならない(※3)。

さて、スクリプトをscilab本体にロードしてみて、音を出してみよう。

playsnd(w);

ビックリするんじゃないだろうか。減衰振動の波形を足し合わせただけ、なのに「鐘の音」みたいになってるだろ?

w1、w2、とか個別の音も聞いてみればいい。場合によっては「可聴域外」なんで音が出ない、って事もあるだろうが、いずれにせよ、それぞれは単独には「音が小さくなっていくサイン波」に過ぎないだろう。ところが「全部足し合わせると」鐘の音っぽくなる。

これが「倍音加算」と言うやり方だ。

倍音合成で作った「鐘」、wの冒頭9,000のサンプル波形。21個の様々なサイン波を足し合わせるだけで凄く複雑な波形が生成されてる事が分かるだろう。

さてさて。いわゆる「科学の実験」としては面白い実験だったと思う。

問題は、だ。

鐘の音を生成するだけで「21個の波形を足し合わせる」とか相当面倒くさい(笑)。

「楽器として」限られたスペース内で「各種パラメータを操作」して「音を作る」ってのは相当大変だ、って想像出来ないか(笑)。

そう、かなり大変なんだよ。だから倍音加算方式のシンセサイザーは人気が出なかったんだ(笑)。

前回チラっと紹介した、往年の河合楽器製のシンセ、KAWAI K3。フーリエ解析をマトモに学んだ人なら「128個のサイン波しか足せないなんてショボ!」とか思うかもしれんが(数学的には無限に足し合わせる・笑)、実際問題として21個足すだけでも大変なのに128個なんて論外だ、と思ってくれる人の方がこの記事の読者では多い事を望む(笑)。ぶっちゃけ、このシンセが日本で大きな性交成功をおさめなかった原因はこの「倍音加算方式」のメンド臭さの為だ。

1975年に商用化が実現したデジタルシンセサイザーだったんだけど、この「音作りの面倒くささ」でイマイチ評判が悪かったんだ。いや、「理屈は簡単」なんだよ(笑)。これほど明解な手法はない、ってば無いし、「減算しかしようがない」アナログ・シンセサイザーに比べると格段に「デジタルの利点」を証明してはみせた。

ただ、「理屈は簡単」でも「ミュージシャンが扱う」には、単に面倒くさかったんだよな(笑)。パラメータを弄って合成して・・・しかも「最終的にどういう波形になるか」っつーのも想像しづらい。結果、アナログ・シンセサイザーみたいに「元々ある波形」から「何かを引いていく」方が分かりやすかったんだよな。

さて、次に出てくるのが、米国スタンフォード大学(※4)が研究・開発した音声合成方式で、結果、世界を席巻した方法論だ。

ところが実は、スタンフォード大学が発表したこの方式に対して、アメリカの楽器メーカーは全く興味を持たなかったそうだ。唯一興味を持ったのが海を渡ってやってきたヤマハの技術者だけ、だったらしく、ヤマハはその「新開発」の音声合成方式に将来性を見出し、スタンフォード大学と契約を結んで特許を取得する。

そう、それが今回のテーマであるFM音源、だ。

ヤマハDX-7(1983年)。世界的に大ヒットしたデジタルシンセサイザーで、FM音源が奏でる音色は当時のポップスを席巻した。

ヤマハは最初、(クソ高い・笑)エレクトロニックピアノの音源としてFM音源を使ったが、1983年にFM音源を搭載したデジタルシンセサイザーDX-7をリリースして、価格の安さの割にはクリアで明るいサウンドで音楽業界に衝撃を与えた。

しかし話はそれだけじゃない、んだ。

ヤマハが開発した「FM音源チップ」はコスパが良く、例えばNEC PC-8801やSHARP X68000、MSXの各パソコン、アーケードゲーム機、セガのメガドライブ等にも搭載される。そう、ヤマハのFM音源チップはビデオゲームの「音」の世界さえも席巻した、と言って良い、爆発的なヒット商品だったんだ。

結果1980年代では、我々はあっちこっちでFM音源が奏でる音を聴くようになる。

ヤマハのFM音源では、上で書いた「オシレータ」を「オペレータ」と呼称している。そしてこのオペレータは殆どのアナログ・シンセサイザーと違い、サイン波しか出力出来ない(※5)。

「あれ、じゃあカワイのシンセと同じく、128個もオシレータを積んでるの?」

と思うかもしれないが、プロ用シンセのラインだと6個しか積んでない。パソコンやゲーム機に組み込まれたチップや、アマチュア用廉価版シンセだとたった4個だ。

「ショボッ!」って思うかもしれんが、全然そんな事はない。FM音源は倍音加算方式とは全く違う音声合成方式なんだ。

FMと言うのはラジオで有名な周波数変調方式(FM)から名前を取ってるが、実際は位相変調方式、って言った方がいい。

ここで位相をちょっと説明する。とは言っても簡単だけどな。

この数式のδを位相、って呼ぶんだ。

つまり、三角関数に与える引数、角度θを2πft + δとした時に、このδが位相となる。そして角度の一部な以上、性質的にはこいつも角度だ。

通常、位相は定数で、三角関数のグラフを右にズラシたり左にズラシたりする効果がある。

高校数学でこういう式を習った事を覚えてるんじゃないか。

この時の左辺の二分のπが要するに位相、だ。

ところが、スタンフォード大学の連中は、この位相に定数ではなく、サイン関数をぶち込めば「複雑な波形を生成する」事を発見した。

これがFM音源、だ。

なお、中にツッコむ側のサイン波を「モジュレータ」、ツッコまれる側のサイン波を「キャリア」と呼称する。分かりづらければモジュレータは男でキャリアは女だ(謎

単純なFM音源では、2つのオペレータ(オシレータ)を用意し、片方をモジュレータ、もう片方をキャリアとし、その2つを直列に組む。

その数式はこうなる。

数式自体は割に単純だが、これがおっそろしく複雑な波形になるんだ。

Scilabで次のようなスクリプトを書いて実行してみよう。

Fs = 44100;
duration = 1;
t = 0:1/Fs:duration;
fc = 220;
fm = 440;
A = 0.1

// FM音源の式
function [x]=FM(fc, fm, beta, t)
　x = A * sin(2 * %pi * fc * t + beta * sin(2 * %pi * fm * t));
endfunction

// FM音源での波形例
w1 = FM(fc, fm, 0.1, t);
w2 = FM(fc, fm, 1, t);
w3 = FM(fc, fm, 10, t);
w4 = FM(fc, fm, 100, t);

// FM音源での音を連続再生する準備
w = [w1, w2, w3, w4];

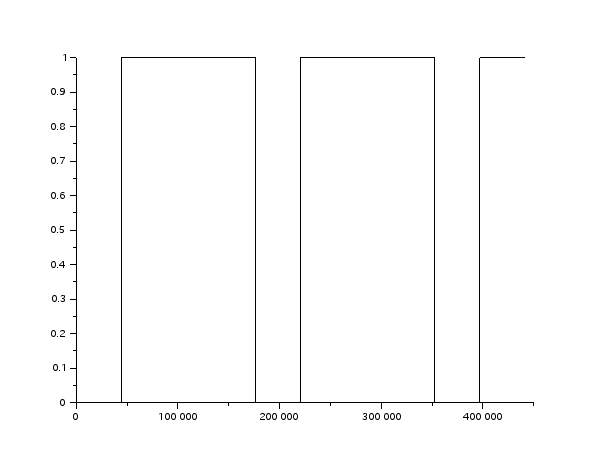
ここではキャリアの周波数を220Hz(A2)、モジュレータの周波数を440Hz(A3)としている。

そしてモジュレータ側の振幅(β)を徐々に上げていってる。

果たして、どうなるか。サウンドを確かめてみよう。

playsnd(w);

最初はサイン波とあまり変わらない音だったのに、w4に近づくに連れ、とんでもない音へと変化していくのが分かるんじゃないか。

w1の波形

w2の波形

w3の波形

w4の波形

どんどん黒くなって行っとる(笑)。取り返しがつかないようになってるが、結局、それだけ複雑な波形へと変化していってるし、同じ波形を書くのも倍音加算方式では難しい、と言う事が分かるんじゃないか。

なお、ここでは2オペレータによる単純なFM音源を解説したが、ゲーム機等に使われてるFM音源は4オペレータで、そのオペレータ同士の「組み合わせ」をヤマハは「アルゴリズム」と呼んでいて、4オペレータ版には8種類の組み合わせを用意してたと思う。

要は「オペレータ同士の組み合わせ」に関してはユーザーの自由度は無い、と言う設計方針だった。

ヤマハの開発したテクニックに「フィードバック」と言うモノがあり、自分自身に変調をかけられる、と言った、プログラミング的には再帰的なテクニックがあり、その再帰回数は最大で7回だ。0の場合はフィードバック無し、って事だな。

また、上のアルゴリズム表を見たら分かるが、変調した波形をまたもやモジュレータとして・・・なんつー事をやってるんで、2つのオシレータ以上に「複雑な波形を生成可能だ」と言う事が分かるだろう。

興味のある人は、上のアルゴリズムをScilabで再現してみてもいいんじゃないか。なお、上のアルゴリズム8が基本的に「4つの波形を用いた」倍音加算方式、に近くなる。

なお、FM音源も、やっぱり「生成する音の予想が付きづらい」と言った性質があり、これも当時のデジタルシンセサイザーならではの特徴だろう。それでも倍音加算方式に比べると格段に「仕組み自体は簡単」なクセに複雑な波形が作れるので、かなり人気のあった音源方式なんだ。

そして世界中のシンセサイザーメーカーがヤマハに太刀打ちできず、ヤマハのFMシンセがブイブイ言ってる間に倒産したメーカーも多い。

日本で販売不振に陥ったメーカーにKORGがある。そして結果、KORGはヤマハの資本参加を受ける事となった。

しかしながら最終的に、KORGは現代の「力技のデジタルシンセサイザー」の礎を開発し販売、それで大成功する。その成功故に長らく君臨してたFM音源シンセにとどめを刺した、と言うのはヤマハにとっては皮肉な話だった。

現代の「PCM音源」をオシレータ化した初のデジタルシンセサイザー、KORG M1(1988年)。これで瀕死のコルグは蘇ったどころか、トップメーカーへと躍り出た。リアルな音源だけでなく、自動演奏機能やエフェクタまで搭載してる、と言う「全て入りマシマシ」状態で、特にアマチュアにとっては初めて「これ一つで満足出来る」シンセサイザーとなり、コルグも自信を持って「ミュージックワークステーション」と呼んでいた。なお、音源波形の数は100種類を超える(アナログ時代を考えると笑っちゃう)。