今週は、Schoemansdal地区の小学校。
今日は、Gr.7で「異分母分数のたし算」です。
実は、この単元は、毎年年度の初めに行うもので、
いまの時期にこれを行うのは、本当は違うのですが、
たまにそういったカリキュラム通りに教えない教師がいます。
前にも書いたとおり、週案を書く習慣のない南アの教師にとって、
指導内容が漏れる可能性が高まるこのやり方は、お勧めできません。
あらかじめ書いておきますが、
今日の話は、算数のちょっと専門的な話なので、興味のある方のみご覧ください。
南アの算数科教育の課題を紹介したいもので。
さっそくですが、今日の問題。
1/3+2/7 (分数のたし算)
これを子どもたちはこのように回答しました。

答えはあっています。
ただし過程は間違っています。お気づきでしょうか?
1/3と2/7を通分するとき、
分母の3と7の最小公倍数である21に揃えます。
そのとき、1/3=1×7/3×7=7/21ですが、上記の回答では、6/21になっています。
(2/7の通分が先にきているからですが‥)
こちらの教師は、答えが合っているので、過程はどちらでもいいと教えていますが、
これを認めると、すぐにうまくいかなくなります。
というわけで私が次の問題を出しました。
4/5-1/4(分数のひき算)
この問題を先のやり方で解くと、次のようになります。

どうでしょうか。
あり得ない順番になったせいで、ひき算ができず、無理やり逆に引いています。
これも答えが合っているので、OKとできますか?
もちろんできませんね。
そこで、何故このような解き方になったかを吟味してみると、
またまた子どものノートから次のような回答を見つけました。
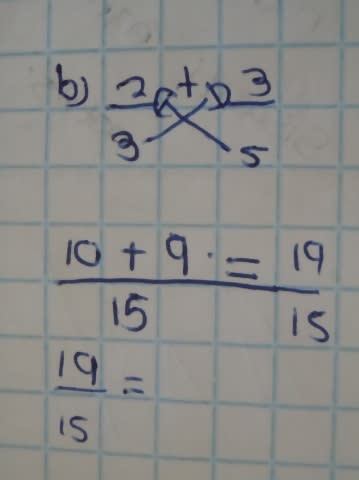
そうです。彼らはクロスして答えを出しているのです。
そのため、最小公倍数として答えを出しているのではなく、
単純に分母同士をかけて答えを出しているわけです。
したがって、クロスを重視するあまり、単純に順番が逆になってしまったと考えられます。
そう考えると、先ほどの回答も納得できます。(再掲)

本当なら分数のたし算をする際に、何故通分するのかなどを分かりやすく教えたいのですが、
こちらの現場の教師の多くが、
答えがあっていればそれでいい的な安易な思いで教えています。
これを何とかできないか、私は未だに悩んでいます。
先日、理数科教師としてFET(職業訓練校)で数学を教えている隊員から、
現地の教師は、途中式は書いてなくても(合ってなくても)
答えがあっていれば点を与えていると聞きましたが、
これも結果のみで過程を重視しない南ア人の性格を顕著に表しているような気がします。
最後に、子どもたちのノートは、
教師がどんな教え方をしたか、その結果どの程度理解したかを図る指標です。
今回も子どものノートが
教師の教え方の未熟さを指摘してくれました。
こういうなぞ解きは、私は結構好きです。
現地の先生たちにもぜひ子どもたちのノートから学んでほしいものですね。



















