電卓のすすめ16 からの続きです。
√ や 複利計算などの話は対数とも密接な関係があります。
建設会社の社長さんとお酒を飲む機会がありました。
社長さん曰く
「昔は今のようにパソコンも関数電卓もなかったから手計算だったよ。
掛け算を足し算に、割り算を引き算に、累乗を掛け算にして計算できる対数は便利だった。」
私なんかは対数を使うとかえって頭がこんがらかることもあるのですが、対数は面白いと思います。
酒の席なのに対数で話が盛り上がっていました。
バブルの時は金利7パーセントという、今では考えられない利息がありました。
複利計算で1,000万円を2,000万円にするには何年必要でしょう。
これは
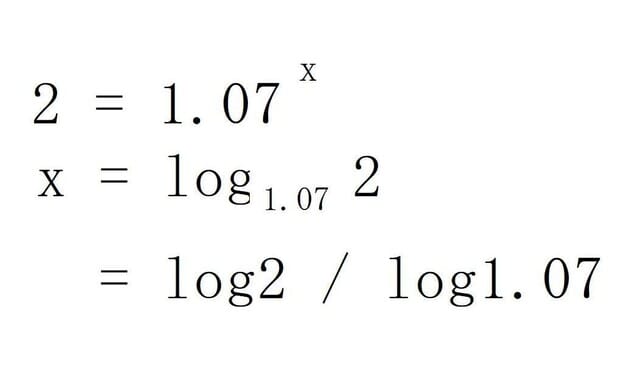
と計算できますので
iPhoneの関数電卓を使って
2[log] [÷]1.07[log][=]

7パーセントの利息で複利計算をすると10年で倍の金額になります。
超大きな数
教えて系の掲示板には次のような質問がありました。
2の2023乗はいくつになるでしょう
これもiPhoneの関数電卓で
とすると

さすがにiPhoneの電卓でも計算できません。
これもlogを使うとある程度の数がわかります。

iPhoneの関数電卓では
2023[×]2[log][=]608.983681228234
logを使って計算すると2の2023乗は609桁の数だと言うことがわかります。
ここから608を引いて
608.983681228234 [-] 608[=][![]() ]
]

2674からはじまる609桁の数であることがわかります。
また
log2 = 0.3010
log3 = 0.4771
log7 = 0.8450
この3つを暗記しておけば
log2 ~ log10 までの値は算出できます。
また、覚える公式も多くありません。

対数も知っていると非常に便利です。
電卓のすすめ18 に続きます。
続編、文具の木の実もご覧ください。










