HP50gで解く算数問題3

問題：台形ABCDの対角線BD上に、点Eを、ADとECが平行になるようにとりました。
三角形「あ」と三角形「い」の面積を求めなさい。
（2012年　女子学院中）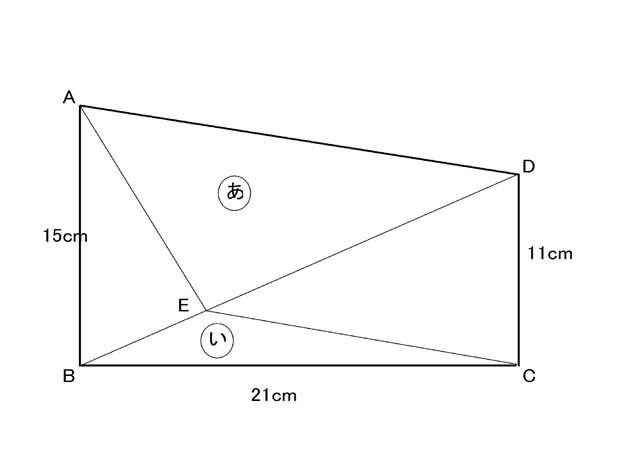



小学校6年生までの知識で解ける問題だが、けっこう難しい。
今回もそのまま解いては面白くないので、複素数を使ってみる。

RPNモードで（□は[SPC]　...「　」は説明文）

0□15i×＋'A[STO] ...「( 0,15)を A に保存」
0□0i×＋'B[STO] ...「( 0, 0)を B に保存」
21□0i×＋'C[STO] ...「(21, 0)を C に保存」
21□11i×＋'D[STO] ...「(21,11)を D に保存」

Eの座標は　DROITE関数　で調べる。


DROITE関数は2つの複素数を引数として直線の方程式を返すため
B□D[CAT][DROITE]　とすると　直線BDのグラフと計算式が現れるので面白い。


HP50gは、その気になれば[STO]で数式も保存しておける。
'BD[STO]

次に
C□(0,4)[CAT][DROITE]　で直線CEの方程式
Y=-.190476190476(x-21)　が表示され、これも保存
'CE[STO]

マトリックスライターを起動しBDとCEの式を入力。
そのままBDと打てば先ほどの式が入力される。

再度マトリックスライターを起動し解きたい変数を入力
'X　'Y
[S.SLB]から[LINSO]でEの値［X=5.6 y=2.93333333333］が表示される。
これを E に保存。
X□Yi×＋'E[STO]


＊面積の計算
ようやくお膳立てができたので面積を計算する。
面積の計算にはCMPLX（右シフト1）のF3にある[CONJ]関数をつかう。

A□D[CONJ]×
D□E[CONJ]×＋
E□A[CONJ]×＋
2/



虚数部の115.5が三角形「あ」の面積である。

同様に三角形「い」の面積をCONJ関数で求めると30.8になる。