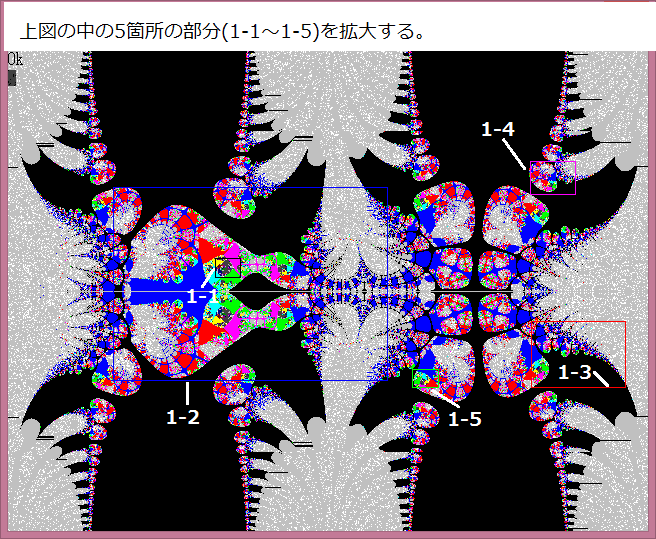今(2015-1現在)から約30年前、在職中にインタープリターBASIC言語を私は覚えさせられた。
当時、たまたま見た科学雑誌に掲載されていた『PCで作る"放散虫”』の記事に私は大変、興味を覚えた。
その記事は本ブログの001記事に書いた、数学者:クリフォード・A・ピックオーバーの論文の簡単な紹介であった。
その論文の概要は、その後、『コンピューター・カオス・フラクタル-見えない世界のグラフィクス-』(クリフォード・A・ピックオーバー著、白揚社)という本の中で紹介されている。
私は、この本を購入する以前より、上記した科学雑誌の記事に基づいて、"放散虫"作り遊びを開始した。
その記事には、インタープリターBASICによる、"放散虫"作りプログラムが簡単に紹介されていたから、私でも其の遊びが可能だった。当時は東芝・パソピ゜アで此の絵作り遊びを開始したものだ。
***
その後、上記した本を買い、自分なりに其の絵作り遊びを続けた。
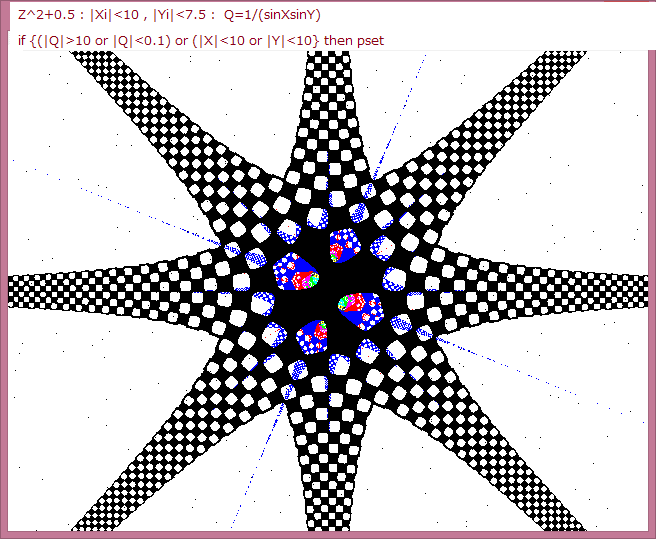
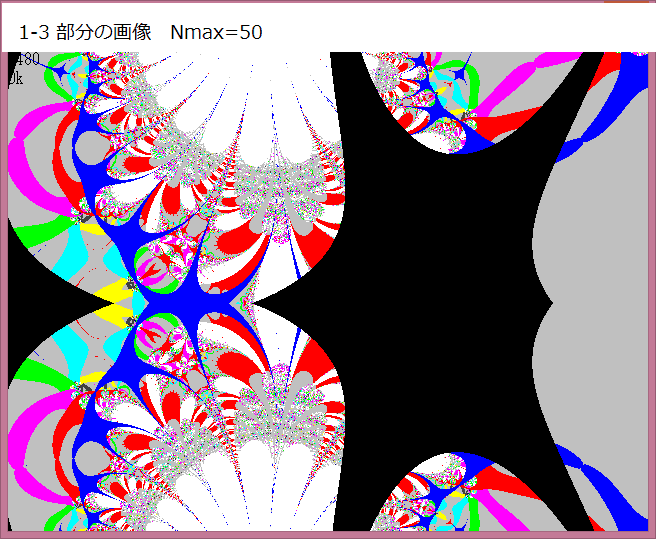
科学雑誌に掲載された"放散虫"は、複素関数がZ^3+0.5という単純なモノだったが、私は複素関数を更に拡張させていった。また画像の作成条件も拡張させていった。
爾来、約30年、私は此の絵作り遊びを続けた。
それは、まさに、クリフォード・A・ピックオーバーが上記の本で書いてあるとおりの楽しさだった。
その楽しさとは、001記事でも紹介したが、このブログの最後に再び、クリフォード・A・ピックオーバーの言葉を以下に引用しておこう。
----------------------------------------------------------------
『私はときどき自分を釣り師になぞらえてみる。コンピューター・プログラムとアイデアは釣り針であり、リールである。コンピューターで描きあげた絵はトロフィーであり、うまいご馳走である。釣り師には、何が釣れるかがいつもわかっているわけではない。しかし、どこがよく釣れるか、どの流れに魚がたまっているか、などについての知識はもっているだろう。しばしばびっくりするほどの大物が釣れるが、これこそまさに釣りの醍醐味である。しかし保証はない。そのかわり予期しない楽しみもある。読者もぜひ未知の釣り場で実際に糸を垂れてほしい。できれば釣りあげた獲物を観賞し更に其れを解剖し内部の構造を調べてほしい。』
-------------------------------------------------------------
このブログでの私の絵作り遊びは、私のネタ切れで終了するが、このブログを見た誰かが、ピックオーバーの書いているような遊びの精神で、このような絵作りに挑戦することを私は期待したい。私の知らない世界が未だ未だあるに違いないからである。