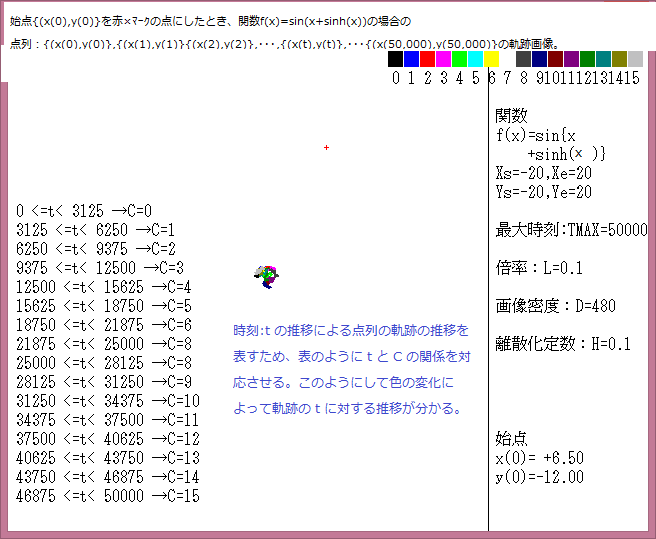
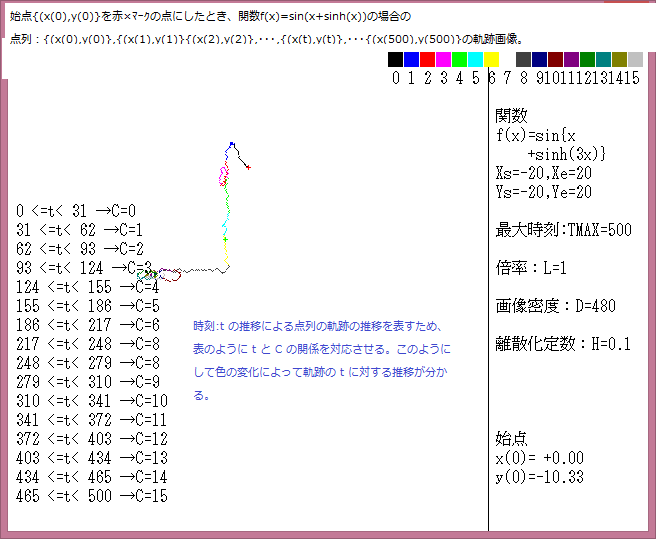
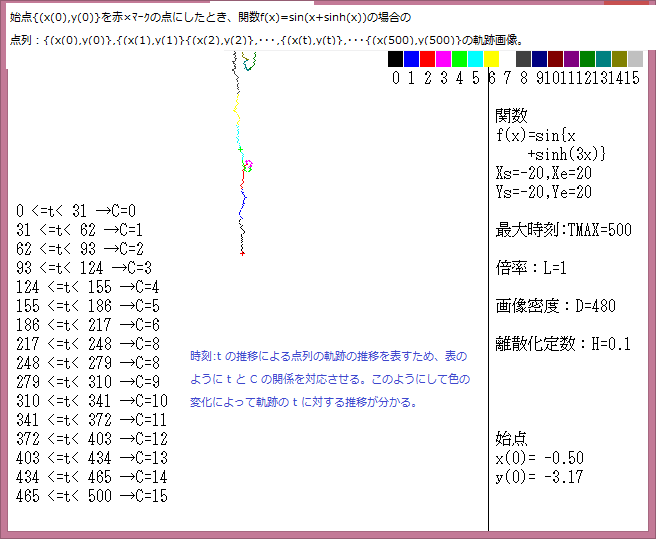
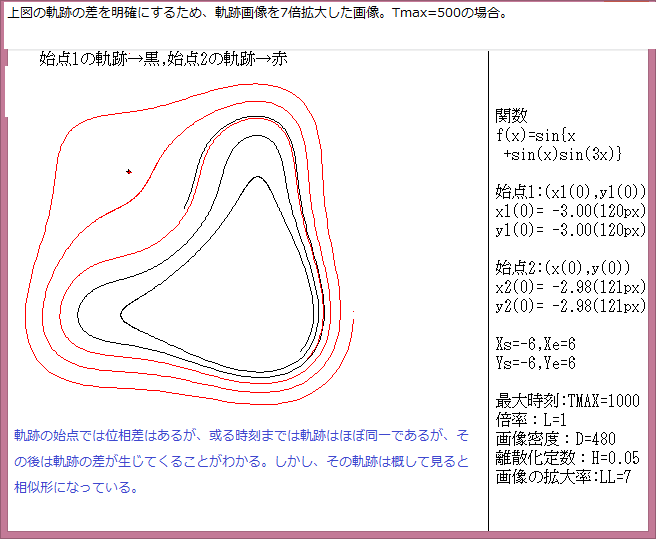
下図は、 関数:f(x)={x^6+(sin(3x)^4}の場合の軌跡の濃度分布画像である。(此の記事の画像の説明及び各パラメーターの説明は記事541参照。)
位相平面の各座標の軌跡通過数を m としたとき、
(a)色:C=m mod 16
(b)色:C=log(m) mod 16
を比較する。
(a)の場合の m 色コード:Cの順序どおりになる。
但し、m=0の場合はプログラムで白としており、C=7(白)の場合は C=8(灰)としている。
mod を使用しているから、m は16進で変化する。
(b)の場合はm=e^C だから、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
以下に示す(b)の画像の色から分かるように、m は 16 以上となっており、C=0~15が16進で表示されるため結果として画像の色が混濁してしまい、画像の色構造が不鮮明となってしまっている。
(b)の画像では、log 効果により色が整理され、その結果、画像の色構造(即ち、軌跡の通過濃度分布構造)が判然としてくる。
以下に(a)(b)を対比した画像を示す。
--------------------------------------



---------------------------------------


位相平面の各座標の軌跡通過数を m としたとき、
(a)色:C=m mod 16
(b)色:C=log(m) mod 16
を比較する。
(a)の場合の m 色コード:Cの順序どおりになる。
但し、m=0の場合はプログラムで白としており、C=7(白)の場合は C=8(灰)としている。
mod を使用しているから、m は16進で変化する。
(b)の場合はm=e^C だから、
C=0(黒)ならば m=e^0.5=1
C=1(青)ならば m=e^0.5~1.5=1~4
C=2(赤)ならば m=e^1.5~2.5=4~12
C=3(橙)ならば m=e^2.5~3.5=12~33
C=4(緑)ならば m=e^3.5~4.5=33~90
C=5(青)ならば m=e^4.5~5.5=90~247
C=6(黄)ならば m=e^5.5~6.5=247~665
C=8(灰)ならば m=e^6.5~8.5=665~4915
となる。但し、m=0 の場合は白としている。
以下に示す(b)の画像の色から分かるように、m は 16 以上となっており、C=0~15が16進で表示されるため結果として画像の色が混濁してしまい、画像の色構造が不鮮明となってしまっている。
(b)の画像では、log 効果により色が整理され、その結果、画像の色構造(即ち、軌跡の通過濃度分布構造)が判然としてくる。
以下に(a)(b)を対比した画像を示す。
--------------------------------------



---------------------------------------