PCが描く奇妙な画像集(数学的万華鏡と生物形態等の世界)

・インタープリタBASICによるフラクタルとカオスの奇妙な画集。

674 Z^3+0.5画像(pset条件の変更)及び拡大画像

2014-11-26 07:45:54 | ジュリィア集合の変形：Z^f(Z)関連


上図の画像作成条件は以下のとおり。(記事186参照)

・複素関数：e^Z+0.5
・N-loop脱出条件：Q=1/(log|X|log|Y|),(|Q|＞10 or |Q|＜0.1)
・pset条件：log|X|＞log|Y|

上図の中の部分を下図のように選び、それを拡大する。





-------------------------







657 Z^(e^sinh Z)+0.1画像の拡大図

2014-11-10 13:44:22 | ジュリィア集合の変形：Z^f(Z)関連
下記の条件の画像の中の部分を拡大する。

・複素関数：Z^(e^sinh Z)+0.1
・N-loop入力条件：|Xi|＜π,|Yi|＜0.75π
・N-loop脱出条件：Q=1/(log|X|log|Y|),|Q|＞10 or |Q|＜0.1
・pset条件：|X|＜10 or |Y|＜10 :色C=No mod 16,C=7→8:N-loop貫通時→灰色

下図が上記の画像である。



上図の中の拡大部分を下図のように選ぶ。





下図が各拡大画像である。











---------------------
関連記事：144






656 Z^(e^sinh Z)+1画像の拡大図

2014-11-09 13:20:52 | ジュリィア集合の変形：Z^f(Z)関連
下記の条件の画像の中の部分を拡大する。

・複素関数：Z^(e^sinh Z)+1
・N-loop入力条件：|Xi|＜π,|Yi|＜0.75π
・N-loop脱出条件：Q=1/(log|X|log|Y|),|Q|＞10 or |Q|＜0.1
・pset条件：|X|＜10 or |Y|＜10

下図が上記の画像である。



上図の中の拡大部分を下図のように選ぶ。





下図が各拡大画像である。











---------------------
関連記事：144






655 Z^(e^sinh Z)+0.46画像の拡大図

2014-11-08 14:25:01 | ジュリィア集合の変形：Z^f(Z)関連
下記の条件の画像の中の部分を拡大する。

・複素関数：Z^(e^sinh Z)+0.68
・N-loop入力条件：|Xi|＜π,|Yi|＜0.75π
・N-loop脱出条件：Q=1/(log|X|log|Y|),|Q|＞10 or |Q|＜0.1
・pset条件：|X|＜10 or |Y|＜10

下図が上記の画像である。



上図の中の拡大部分を下図のように選ぶ。





下図が各拡大画像である。(1-5は省略)









---------------------
関連記事：144






609 Z^f(Z)+C 画像 (その４)

2014-10-01 09:10:26 | ジュリィア集合の変形：Z^f(Z)関連
下図は以下の画像である。

・複素関数は、Z^f(Z) で、f(Z) は、Z^2, Z^3, Z^5, Z^6, Z^7 の 6 種類。

・N-loop脱出条件は、『もし、(X^2+Y^2)＞100 ならば脱出する』。　

・pset条件は、『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』。

下図は、上記条件の 6 種類の関数の画像の一括表示したもので、下図の上段左より、f(Z)= Z^2, Z^3, Z^4　。下段左より、f(Z)=Z^5, Z^6, Z^7。



次に、f(Z)=Z^5, Z^6, Z^7 の画像を個別示す。







608 Z^f(Z)+Ｃ 画像 (その３)

2014-09-30 11:10:23 | ジュリィア集合の変形：Z^f(Z)関連
下図は以下の画像である。

・複素関数は、Z^f(Z) で、f(Z) は、前記事同様、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。

・N-loop脱出条件は、『Q=1/(log|X|log|Y|)として、もし、(|Q|＞10 or |Q|＜0.1 ならば脱出する』。　

・pset条件は、『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』。

下図は、上記条件の 6 種類の関数の画像の一括表示したもので、下図の上段左より、f(Z)= sin Z , cosh Z, e^Z　。下段左より、f(Z)=Z^2, Z^3, Z^4。



次に、6 種類の関数の画像を個別に紹介します。
sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。














607 Z^f(Z)+C 画像 (その２)

2014-09-30 07:35:21 | ジュリィア集合の変形：Z^f(Z)関連
下図は以下の画像である。

・複素関数は、Z^f(Z)+C で、f(Z) は前回同様　sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。

・N-loop脱出条件は『Q=tan(XY)として、もし、(|Q|＞100 or |Q|＜0.01 ならば脱出する』。　

・pset条件は『N-loop脱出後、もし、(|X|＜10 or |Y|＜10)ならば、psetする』。

下図は、上記条件の 6 種類の関数の画像の一括表示したものである。
下図の上段左より、f(Z)= sin Z , cosh Z, e^Z　。下段左より、f(Z)=Z^2, Z^3, Z^4。



次に、6 種類の関数の画像を個別に、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。













606 Z^f(Z)+C 画像 (その1)

2014-09-29 06:54:48 | ジュリィア集合の変形：Z^f(Z)関連
下図は以下の画像である。

1.複素関数：Z^f(Z)+o.5 にて、上図上段左より、f(Z)=sinZ , coshZ , e^Z　下段左より、f(Z)=Z^2 , Z^3 , Z^4
2.N-loop脱出条件：もし、X^2+Y^2＞100　ならば脱出する。
3.pset条件：もし、(|X|＜10 or |Y|＜10) ならばpsetする。



下図は、上図の上段右画像の縮小・拡大図である。
即ち、N-loop入力：|Xi|＜1.5L , |Yi|＜0.75L にて、
上図上段左より、L=0.5 , 0.8 ,1　下段左より、L=2, 3, 4



***

下図は以下の画像である。
1.複素関数：Z^(e^Z)+o.5
2.N-loop脱出条件：もし、X^2+Y^2＞100　ならば脱出する。
3.pset条件：もし、(|X|＜10 or |Y|＜10) ならばpsetする。


147 Z^(e^sin Z) +1 の親子画像

2014-07-09 08:13:38 | ジュリィア集合の変形：Z^f(Z)関連
今回の画像作成条件は、以下のとおり。

・複素関数：Z^(e^sin Z) +1
・N-loop脱出条件：Q=1/(log|X|log|Y|)として、|Q|>10 or |Q|<0.1 のとき　　　　脱出する。
・pset条件：|X|<10 or |Y|<10 のとき、psetする。

この画像の中の4箇所を選び(それを子1～子4と名づける)、それらを拡大する。

<img src="http://blogimg.goo.ne.jp/user_image/51/35/3e797a00f380a4437cc09b3c70375bfc.jpg">





------------------------------------------------







095 Z^(sinZ)画像のフラクタル性 (その3)

2014-07-05 11:46:28 | ジュリィア集合の変形：Z^f(Z)関連
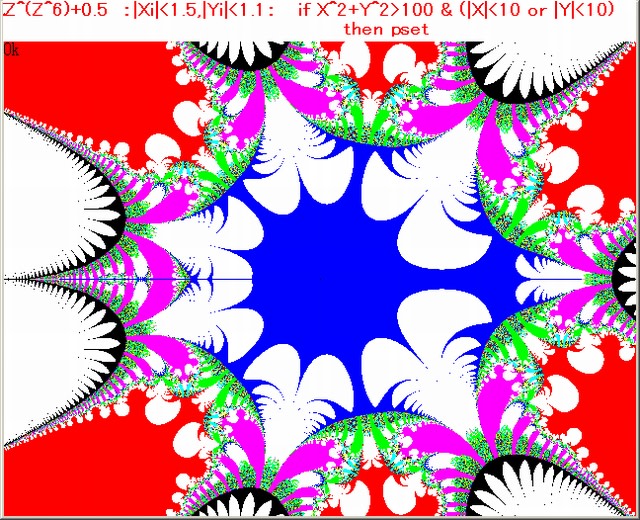
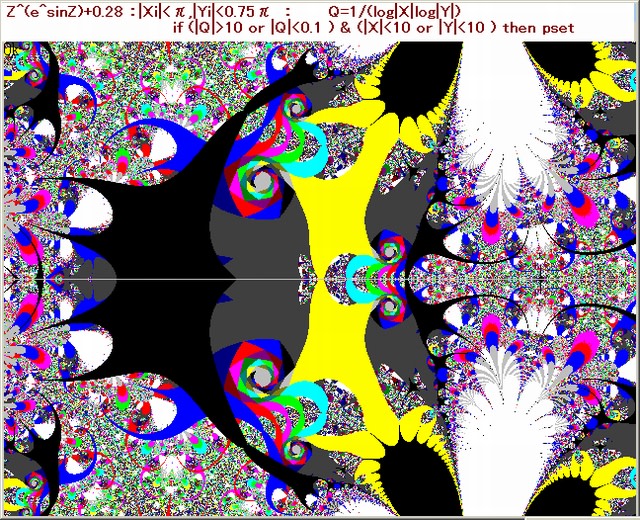
以下の図1の画像は前記事094における5代目の画像である。
画像作成条件は前記事と同じ。図1の中の A 部の黒枠部分を拡大し其れを6代目の画像と名づける(図2)。
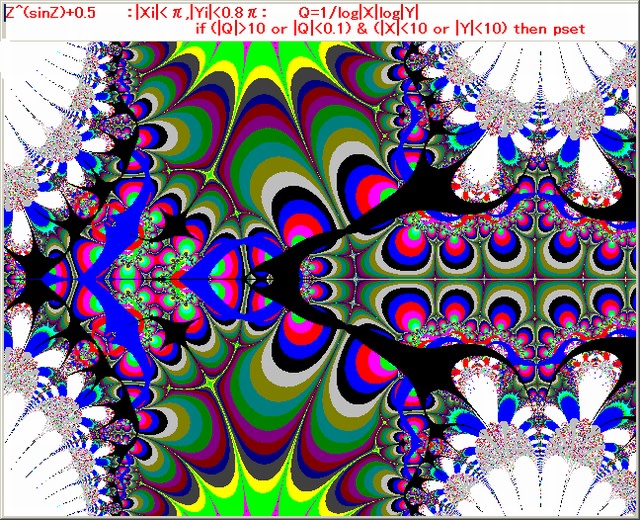
図2は其れ以前の代の画像と自己相似(フラクタル)な画像となっていることが分かる。



-----------------------------------------------------------------
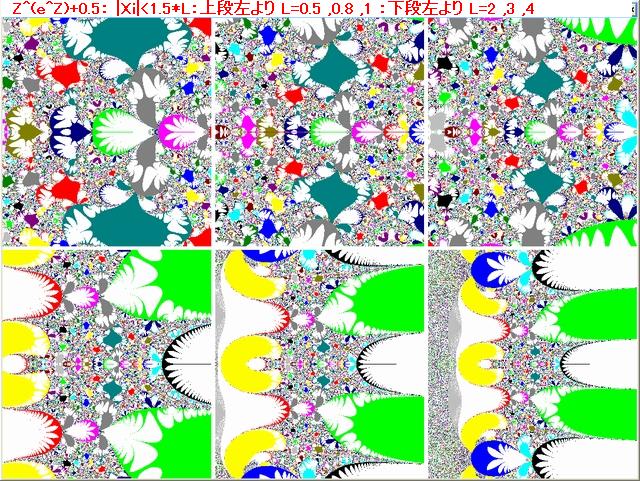
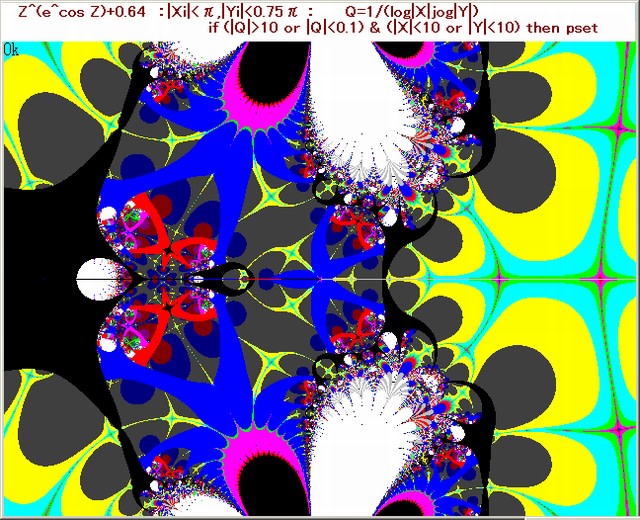
以下の画像は、5 代目の画像の中の別の部分を拡大した画像である。
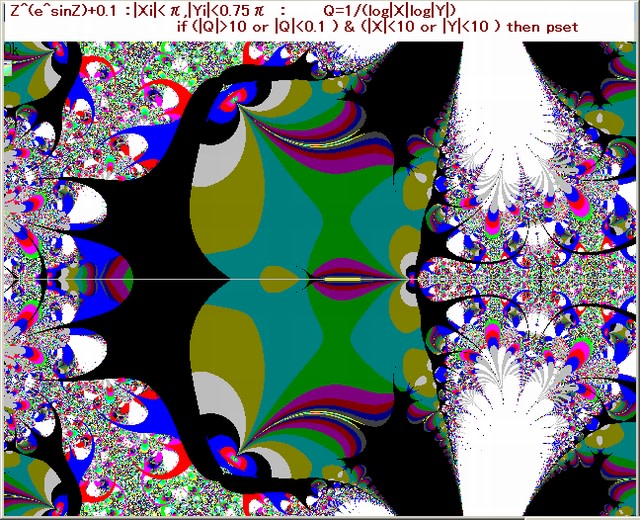
図3の B の黒枠部分を拡大する。拡大した画像が図4。この図4も6代目の画像となる。
この図も其れ以前の代の画像と自己相似(フラクタル)な画像となっている。
但し図4はN-loopのNmax=1000としている。以前の図はNmax=100である。
また図4はN-loop貫通時の色は黒(C=0)にしている。以前の図は暗い白(C=15)である。



-----------------------------------------------------------------
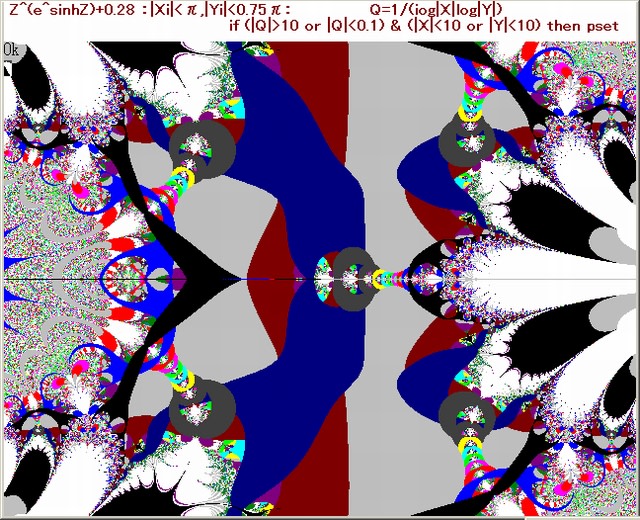
以下の画像はN-loopのNmaxが100の場合と1000とした場合に画像に変化があるかどうかを調べた画像である。
図5がNmax=100の場合と図6がNmax=1000の場合である。
両図は、ほとんど(というより全く)変化がない。
従って画像作成条件でのNmaxは100で充分であることが分かる。



094 Z^(sinZ)画像のフラクタル性 (その2)

2014-07-05 11:07:55 | ジュリィア集合の変形：Z^f(Z)関連
(以下の画像の作成条件は、前記事093と同じ。

1.複素関数：Z^(sinZ)+0.7 。
2. N-loop脱出条件：Q=tan(XY),(|Q|＞100 or |Q|＜0.01)　
3. pset条件：|X|＜10 or |Y|＜10

N-loop入力範囲：|Xi|＜π,|Yi|，0.75πの画像(図1)を一代目と名づける。
その一代目画像の中の一部分を選び、それらを拡大し、それを二代目(図2)と名づける。
そして、その二代目画像の一部分を選び、再び、それを拡大する。
その画像を三代目(図4)と名づける。同様なことを五代目(図8)まで続ける。

それらの各画像は其れ以前の画像と自己相似性(フラクタル性)になっていることが分かる。

このテの画像の自己相似性(フラクタル性)は、複素関数は違うが
記事010で調べているので其れを参照。
---------------------------------------------















093 Z^(sinZ)画像のフラクタル性 (その1)

2014-07-05 10:30:25 | ジュリィア集合の変形：Z^f(Z)関連
1.複素関数：Z^(sinZ)+0.7 。
2.N-loop脱出条件：Q=tan(XY),(|Q|＞100 or |Q|＜0.01)　
3.pset条件：|X|＜10 or |Y|＜10
4.N-loop入力範囲：|Xi|＜π,|Yi|＜0.75π



上図の中の4箇所の部分を下図のように選び其れらを拡大する。




------------------------------------------------------------





-----------------------------------------------------------

1図の中の画像(4図～7図)が、1図とフラクタル画像となっている
ことが分かる。