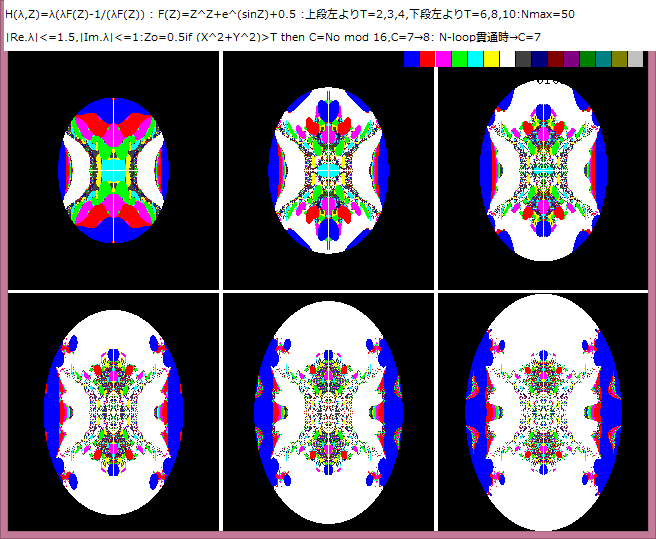
再帰的合成関数画像について復習する。(記事399参照)
----------------------------------------------
λ、Zを複素数とし、λ=LR+iLI , Z=X+iYとする。
今、任意の複素関数:F(Z)として、また複素関数:H(Z,λ)=λ(λF(Z)-1/λF(Z)とする。
ここで、巡回式:Z←H(Z,λ)を考える。
Zの初期値をZ0とする。最大巡回回数をNmaxとする。
この巡回式で、X^2+Y^2>T(実定数)のとき、巡回ループを抜け出すとする。
今、λの複素平面領域:LRS<=LR<=LRE,LIS<=LI<=LIE の各点において、
Z←H(Z,λ)を実行する。此のループを貫通した場合、該当点を黄色とする。
ループを抜け出した時の巡回回数をNoとして、其の該当点を以下の色とする。
C=No mod 16,C=7→8,6→5。



------------------------------






------------------------------
BASIC/98による画像作成プログラムを以下に示す。
10 REM H(Z,λ)=λ(λF(Z)-1/λF(Z))
11 REM F(Z)=Z^Z
20 REM 横軸(K):640 dots、縦軸(J):480 dots
21 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ARCTAN3.BAS",22,ALL
22 CHAIN MERGE "C:\BASIC1\PRO\SUBR\Z^ZA.BAS",23,ALL
23 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR右上表示.BAS",30,ALL
30 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",70,ALL
70 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER1.BAS",80,ALL
80 ON ERROR GOTO 50000
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
120 GOSUB 10000
130 OPEN "C:\BASIC1\RUN\画像DATA.DAT" FOR OUTPUT AS #1
140 OPEN "C:\BASIC1\RUN\親DATA.DAT" FOR OUTPUT AS #2
150 REM 親DATAの設定(随時変更)
160 LRS=-1 :LRE=1 :LIS=-0.5 :LIE=0.5
170 DR=(LRE-LRS)/640 :DI=(LIE-LIS)/480
180 WRITE #2,LRS,LRE,LIS,LIE,DR,DI
190 CLOSE #2
200 FOR J=0 TO 480
210 LOCATE 0,0:PRINT J
211 LI=LIS+DI*J
220 FOR K=0 TO 640
230 X=0.5 :Y=0
240 LR=LRS+DR*K
260 FOR N=0 TO 500
261 R=SQR(X^2+Y^2)
262 GOSUB 5000
263 GOSUB 9000
270 FR=ZZR
280 FI=ZZI
290 A1=LR*FR-LI*FI
300 A2=LI*FR+LR*FI
301 A33=A1^2+A2^2
302 IF A33=0 THEN 490
310 A3=1/A33
320 A4=LR*FR-LI*FI-A3*A1
330 A5=LI*FR-LR*F1+A3*A2
340 HR=LR*A4-LI*A5
350 HI=LR*A5+LI*A4
360 X=HR : Y=HI
390 Q=X^2+Y^2
400 IF Q>500 THEN 440
410 NEXT N
411 C=7:GOTO 470
440 '発散時のPSET
450 C=N MOD 16
460 IF C=7 THEN C=8
470 PSET (K,J),C
480 WRITE #1,K,J,C,N
490 NEXT K
500 NEXT J
501 GOSUB 3000
510 END