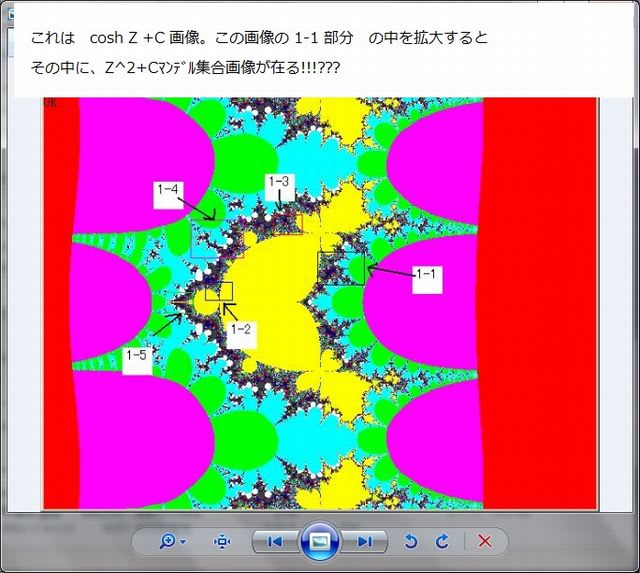
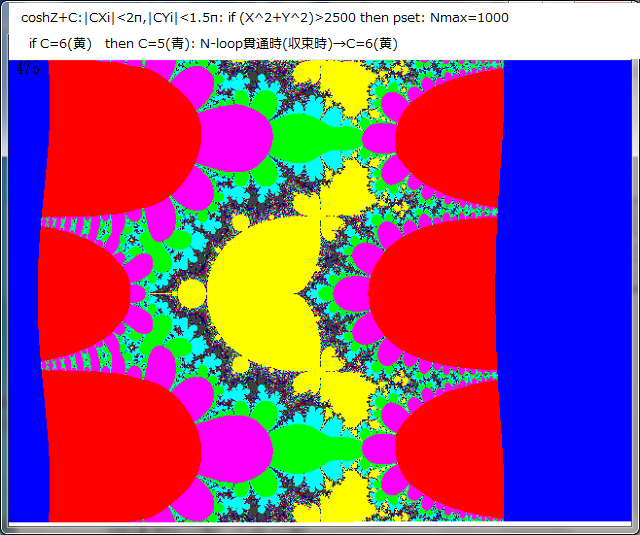
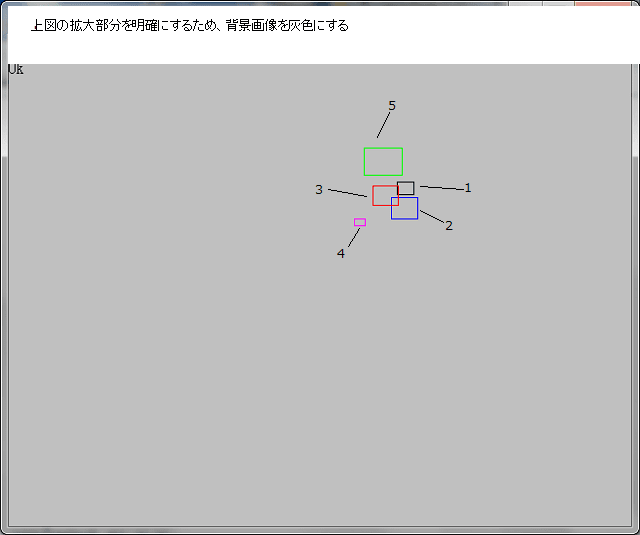
coshZマンデルブロ全体画像の中の1-3の部分を更に5個所拡大する。
先ず、1-5 部分の箇所を再確認する。



-------------------------------------
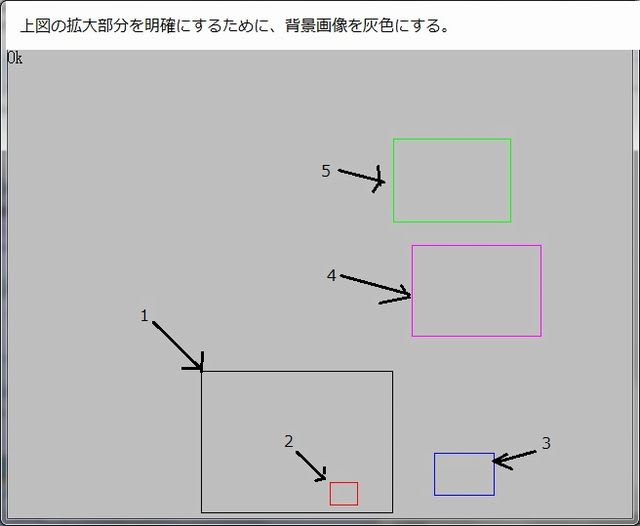
上図の拡大部分にいて以下の5種類のCについての画像を示す。
Noを脱出時のN値としたとき、色Cは以下の5種類の画像を示す。
1. C=No MOD 16
2. C=LOG(No) MOD 16
3. C=4*LOG(No) MDD 16
4. C=15-(4*LOG(No) MOD 16
5. 赤黒縞模様画像
---------------------------------
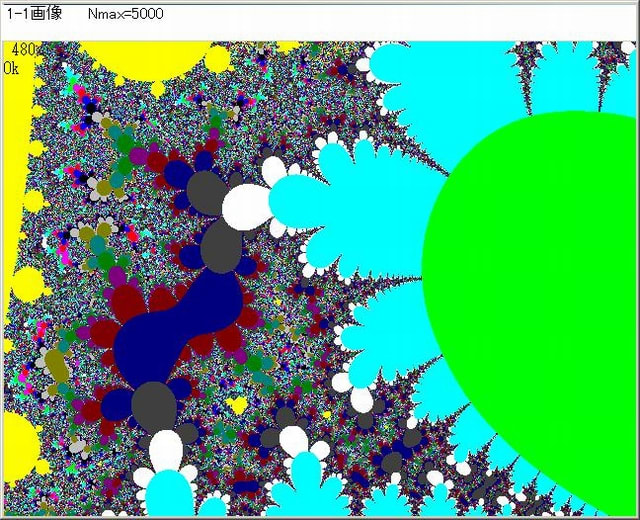
・1-3-1 画像





---------------------------------
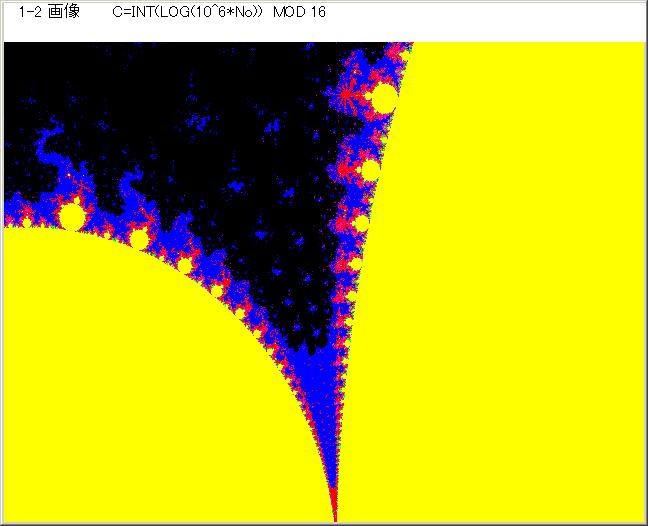
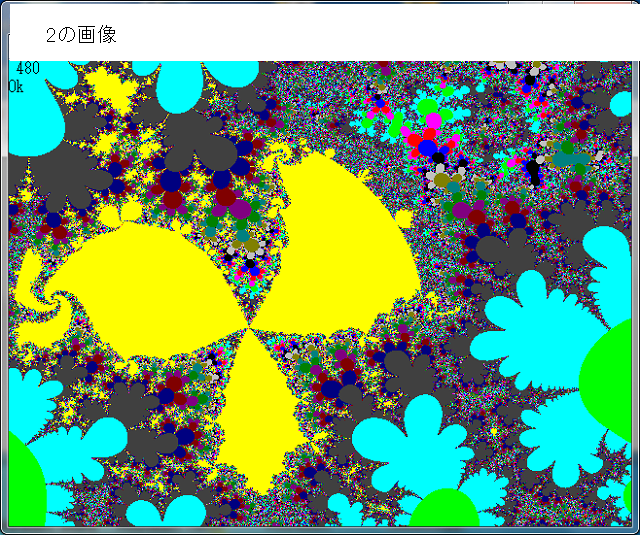
・1-3-2 画像





----------------------------------
・1-3-3 画像





----------------------------------
・1-3-4 画像




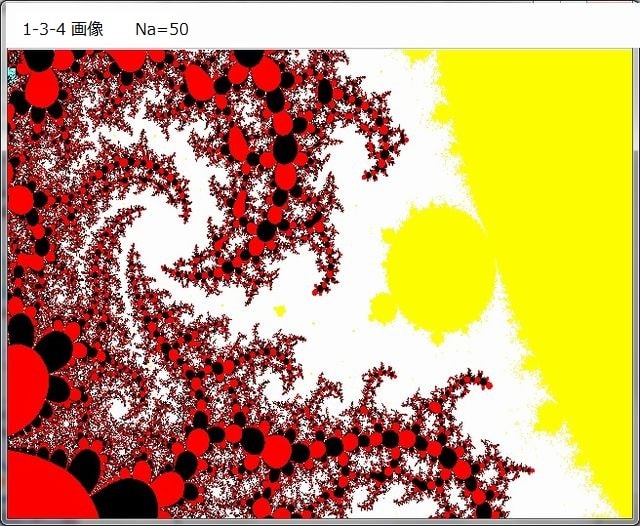
-----------------------------------
・1-3-5 画像





先ず、1-5 部分の箇所を再確認する。



-------------------------------------
上図の拡大部分にいて以下の5種類のCについての画像を示す。
Noを脱出時のN値としたとき、色Cは以下の5種類の画像を示す。
1. C=No MOD 16
2. C=LOG(No) MOD 16
3. C=4*LOG(No) MDD 16
4. C=15-(4*LOG(No) MOD 16
5. 赤黒縞模様画像
---------------------------------
・1-3-1 画像





---------------------------------
・1-3-2 画像





----------------------------------
・1-3-3 画像





----------------------------------
・1-3-4 画像





-----------------------------------
・1-3-5 画像





























































 ---------------------------------------------
---------------------------------------------