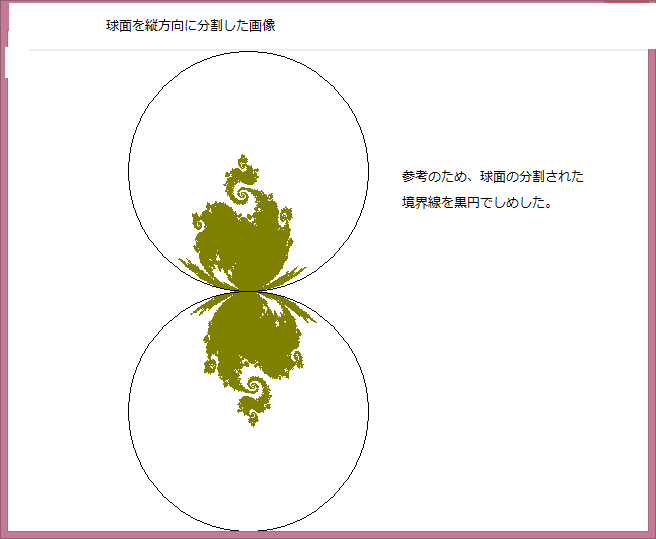
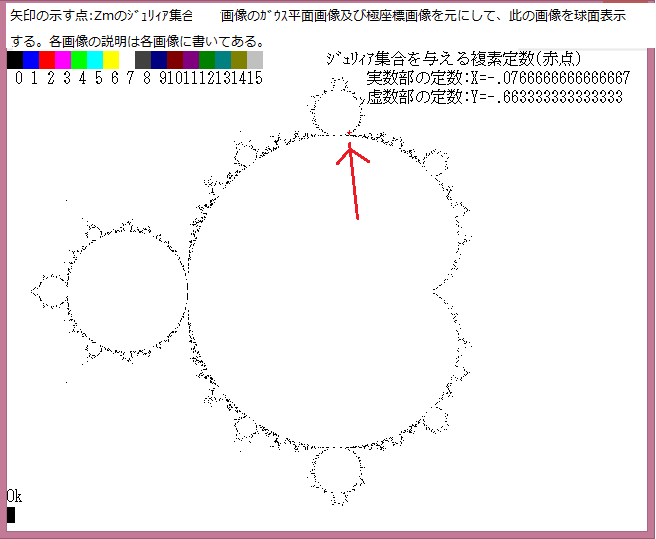
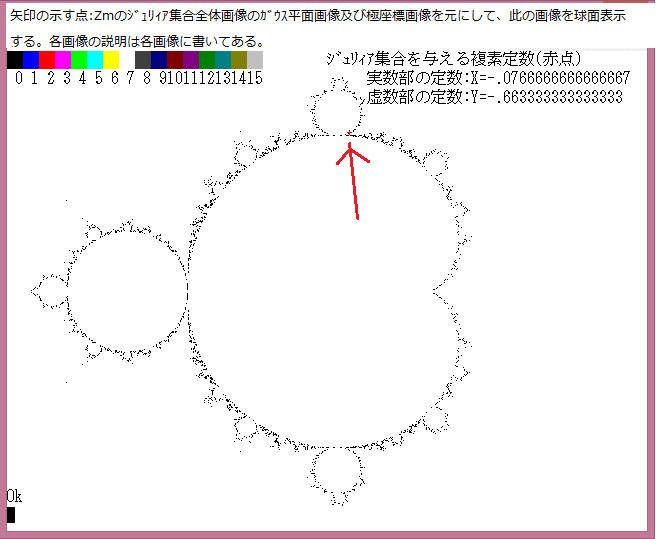
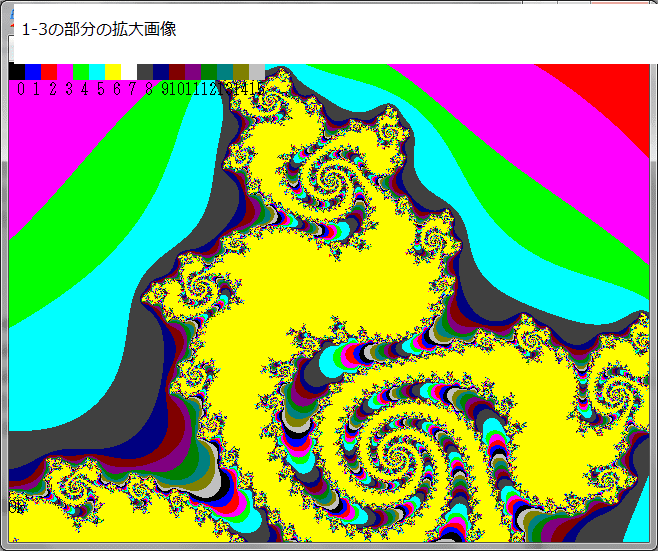
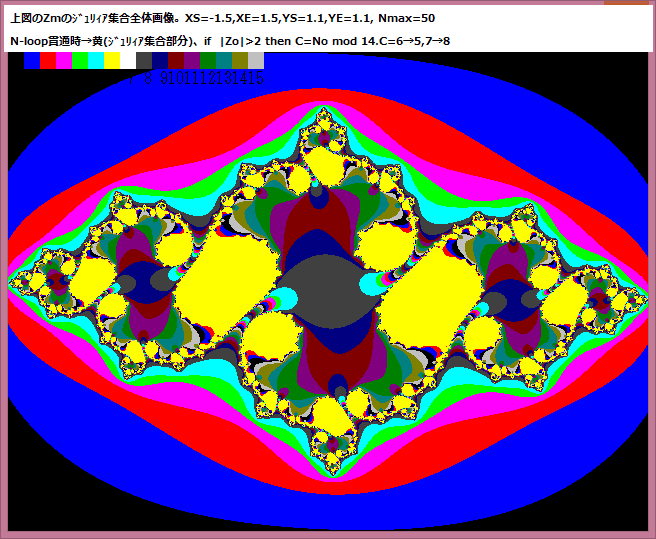
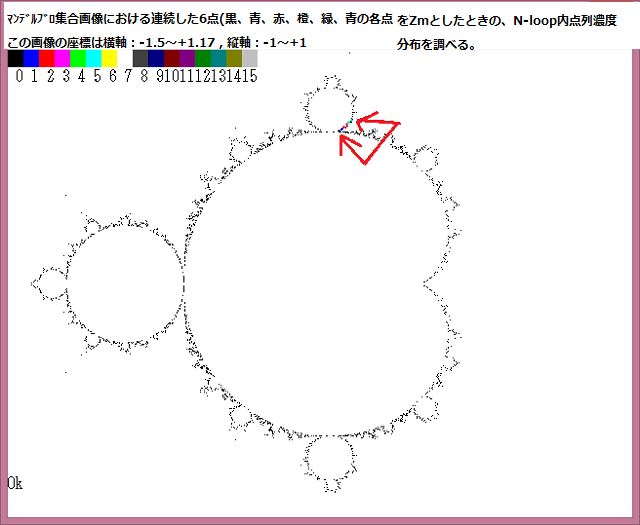
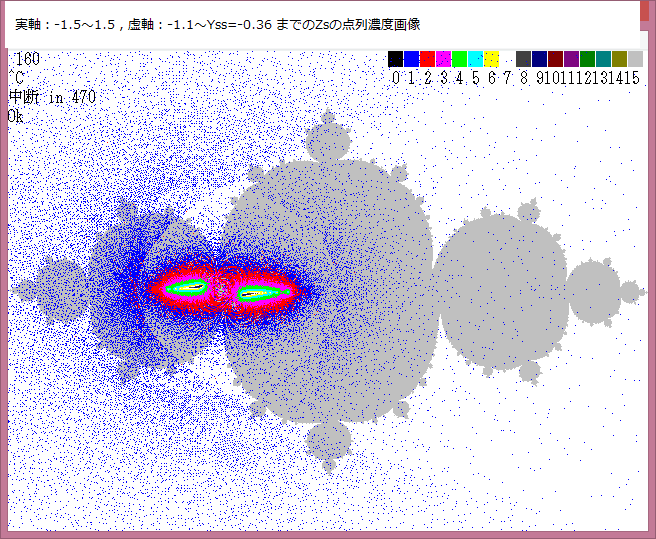
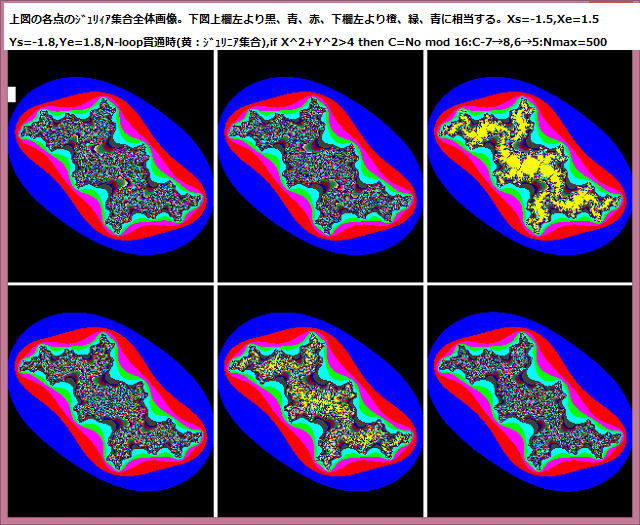
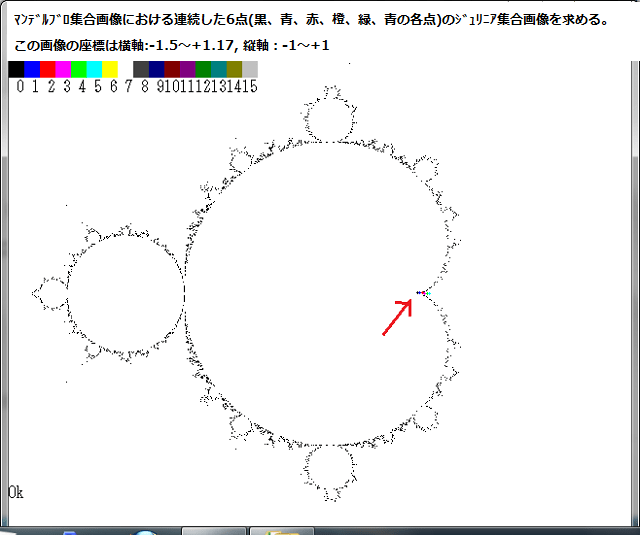
或る与えられた複素平面領域 D の点をZsとする。また任意の複素定数をZmとする。
D の領域は実軸は -1.5~1.5 、虚軸は -1.1~1.1 とする。
ここで、Zsを始点とする再帰点列:Z←Z^2+Zmを考えると次の点列が得られる。
Z0,Z1,Z2,Z3,・・・,ZN,・・・ ・・・(1)
ここで、Z0=Zs^2+Zm ,Z1=Z0^2+Zm,・・・・である。
今、この点列の数の上限を設け其れをNmaxとする。
Nmax以下の或るNoで、|ZNo|>2の場合、点列は発散すると定義する。
また、Nmax以下の如何なるNでも|ZN|










--------------------------------------------------------------------
上図から分かるように、ジュリィア集合内の全てのZsの点列の濃度は、ジュリィア集合画像の特定の部位に集中している。その最大濃度値はC=8だから、m=e^7.5~e^8.5=1807~4914の範囲にある。また点列は領域 D の全域に渡って存在している。青色の部分(C=1)の濃度は、e^0.5~e^1.5=1.6~4.5
の範囲にある。