今までのマンデルブロ画像は通常のZ→Z^2+Cの画像だったが、Z→Z^3+Cのマンデルブロ画像についても調べる。
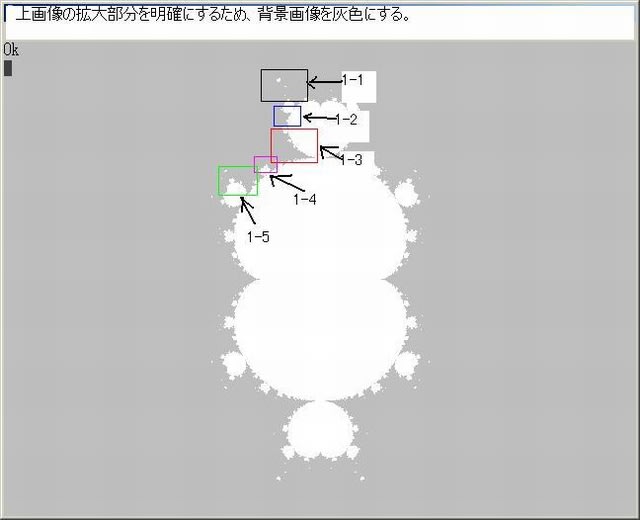
下図は、|CXi|<2,|CYi|<1.5の場合のZ^3マンデルブロ画像である。
Nmax=1000である。N-loop脱出条件は、Q=X^2+Y^2>4としていてZ^2マンデルブロ画像と同じ。
なお此の画像の作成プログラムにおいては、N=NmaxでもN-loopを脱出できない(収束状態とみなす)場合は、特に色は付けていない。従って画像の白い部分はZ^3マンデルブロ集合部分と見なせる。

上図の5箇所の部分を下図のように選び、それぞれ拡大する。

---------------------------------------------------------
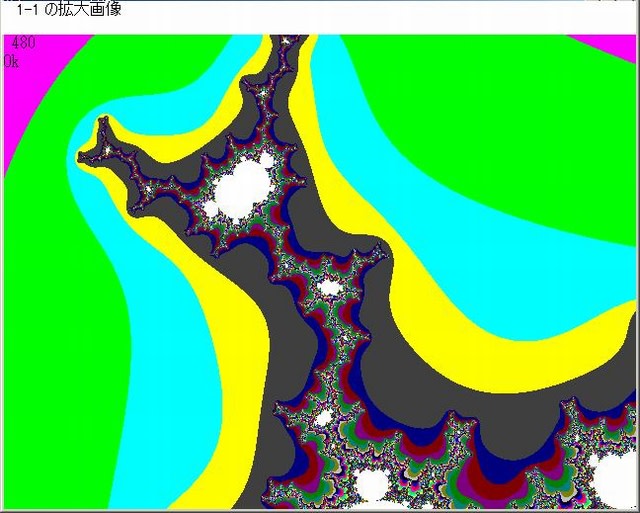
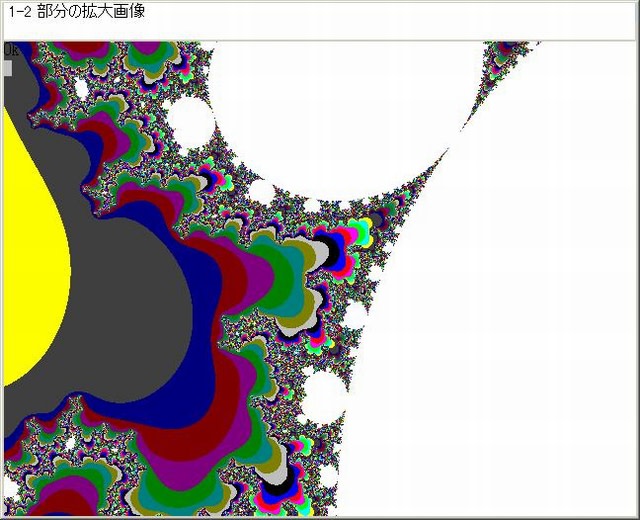

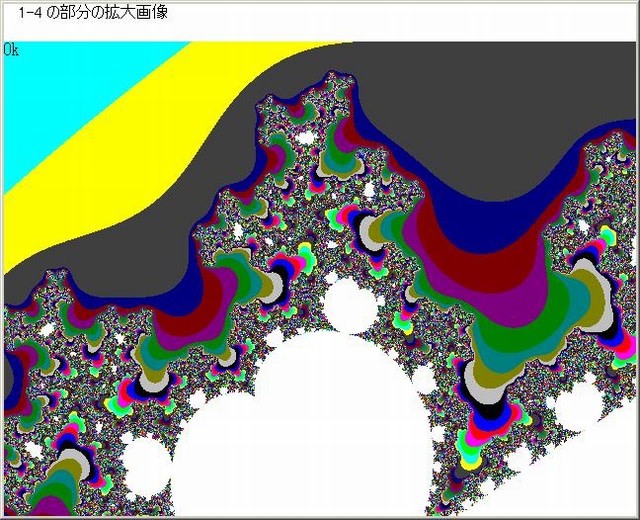
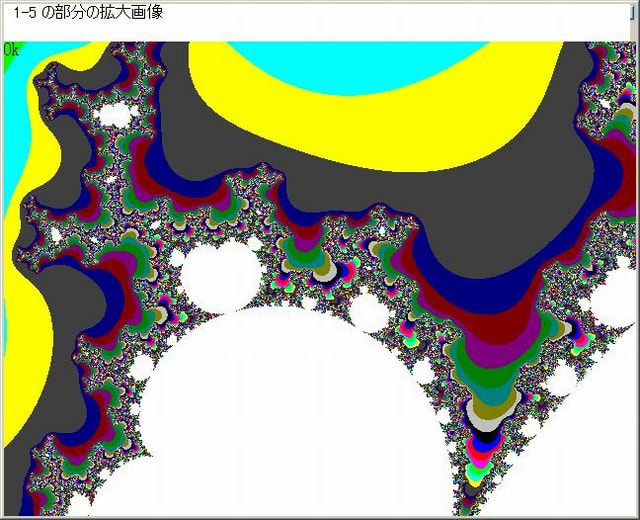
以上の図から分かるように、Z^3+Cマンデルブロ画像においても随所にZ^3ミニ・マンデルブロ集合が存在している。以上の図で、N-loop脱出時のNをNoとしたとき画像の色はC=No MOD 16としている。
Z^3マンデルブロ集合付近の色は混然としていて、つまりNoの変化が激しい。
従ってNoの変化を平坦にするためNoをlog(No)化する。
そうすることによって、Noの変化がグループ化され其の変化の様子が単純化されNoの変化の様子が、より分かりやすくなる。
以下の図はC=INT(LOG10^5*N) MOD 16とした画像である。(画像の上の注記のNはNoのタイプ・ミスである。


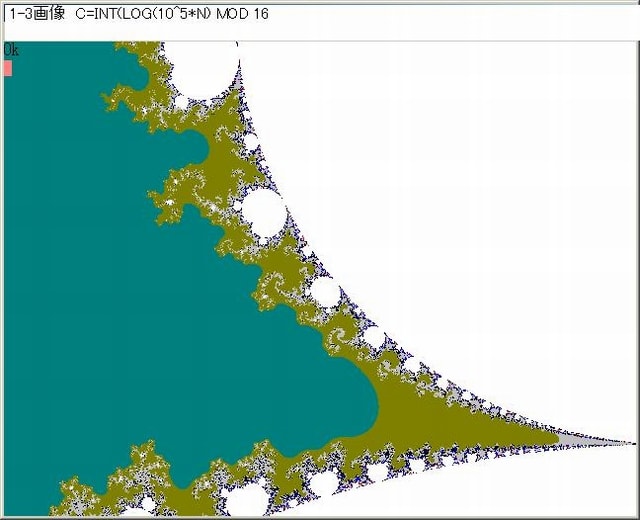
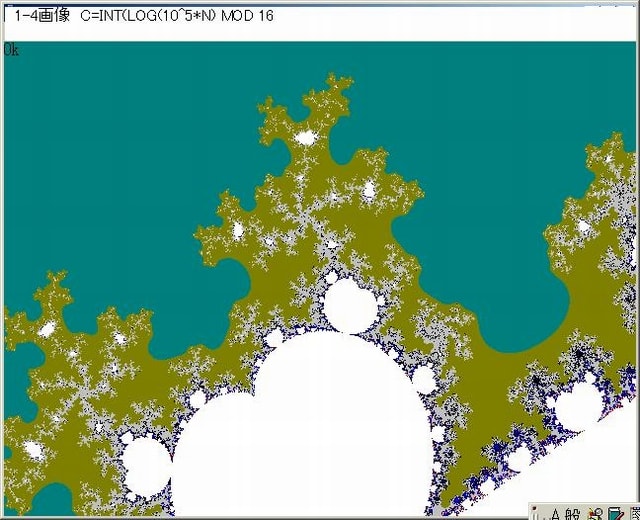

以上の画像のようにNoの変化をlog化して平坦にしてもlog(N)oの変化は複雑な模様になっている。
(画像の上の注記の10^5は色をシフトさせ、配色を分かりやすくするためのもので本質的なものではない)。
このlogNoの画像の模様変化より、マンデルブロ集合付近のNoが、いかに複雑に変化しているかが分かる。このlogNo画像自体が個性的な画像となっている。
以下の図は、No>20場合のみの画像である。色はC=No MOD 16 でオリジナル画像と同じである。


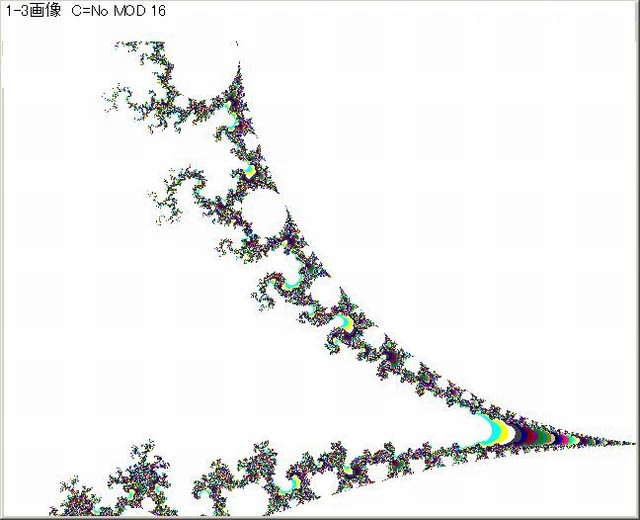
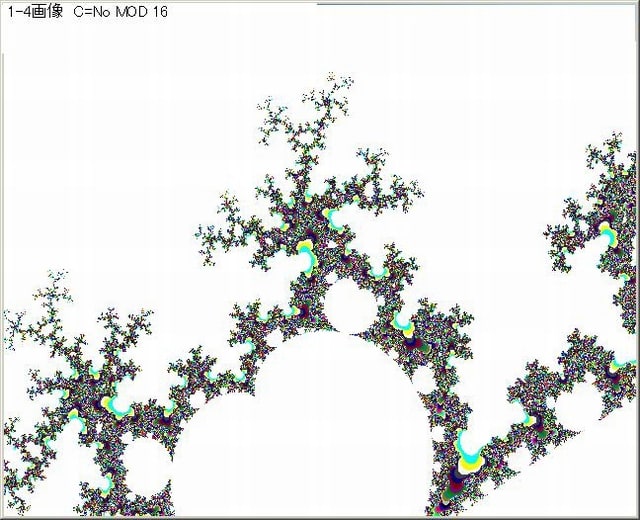

上の図からも、Z^3マンデルブロ集合周辺のNoの複雑さ・混在さが分かる。
またN>20の場合に相当する画像の位置(複素平面の位置(CX,iCY)の模様が枝状に伸びていて、この模様自体も面白い。
下図は、|CXi|<2,|CYi|<1.5の場合のZ^3マンデルブロ画像である。
Nmax=1000である。N-loop脱出条件は、Q=X^2+Y^2>4としていてZ^2マンデルブロ画像と同じ。
なお此の画像の作成プログラムにおいては、N=NmaxでもN-loopを脱出できない(収束状態とみなす)場合は、特に色は付けていない。従って画像の白い部分はZ^3マンデルブロ集合部分と見なせる。

上図の5箇所の部分を下図のように選び、それぞれ拡大する。


---------------------------------------------------------





以上の図から分かるように、Z^3+Cマンデルブロ画像においても随所にZ^3ミニ・マンデルブロ集合が存在している。以上の図で、N-loop脱出時のNをNoとしたとき画像の色はC=No MOD 16としている。
Z^3マンデルブロ集合付近の色は混然としていて、つまりNoの変化が激しい。
従ってNoの変化を平坦にするためNoをlog(No)化する。
そうすることによって、Noの変化がグループ化され其の変化の様子が単純化されNoの変化の様子が、より分かりやすくなる。
以下の図はC=INT(LOG10^5*N) MOD 16とした画像である。(画像の上の注記のNはNoのタイプ・ミスである。





以上の画像のようにNoの変化をlog化して平坦にしてもlog(N)oの変化は複雑な模様になっている。
(画像の上の注記の10^5は色をシフトさせ、配色を分かりやすくするためのもので本質的なものではない)。
このlogNoの画像の模様変化より、マンデルブロ集合付近のNoが、いかに複雑に変化しているかが分かる。このlogNo画像自体が個性的な画像となっている。
以下の図は、No>20場合のみの画像である。色はC=No MOD 16 でオリジナル画像と同じである。





上の図からも、Z^3マンデルブロ集合周辺のNoの複雑さ・混在さが分かる。
またN>20の場合に相当する画像の位置(複素平面の位置(CX,iCY)の模様が枝状に伸びていて、この模様自体も面白い。









