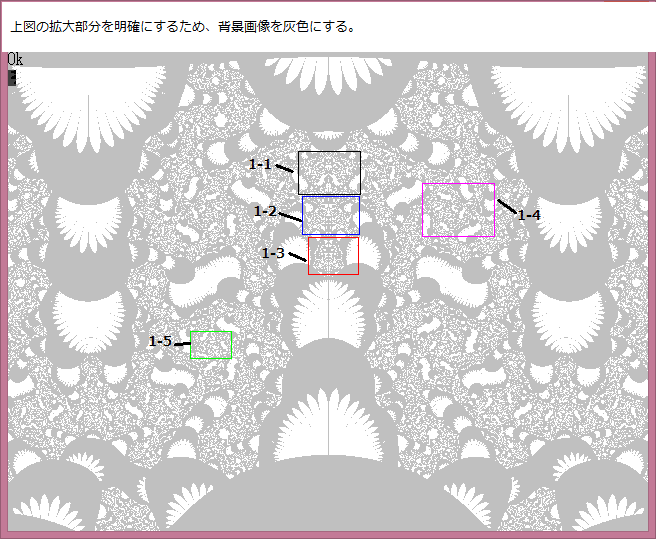
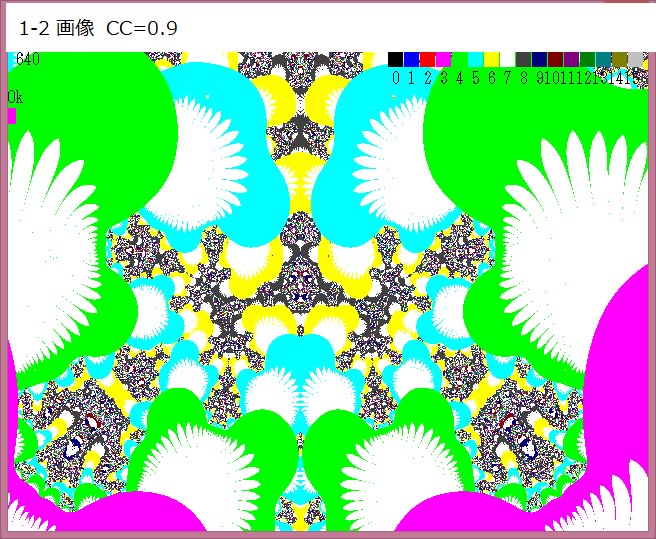
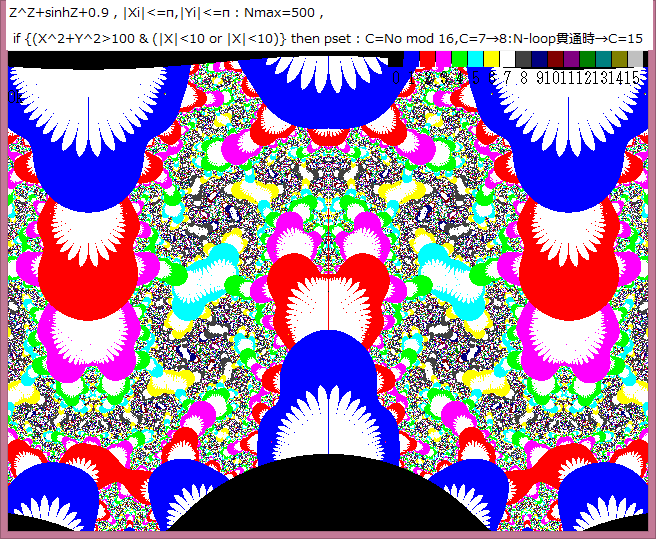
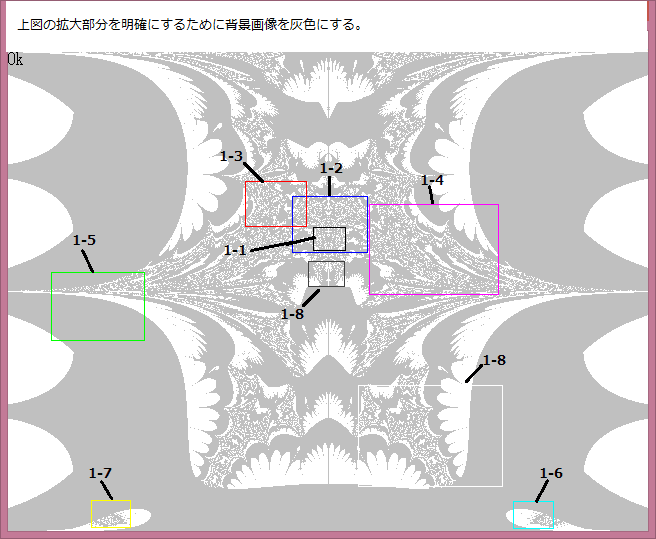
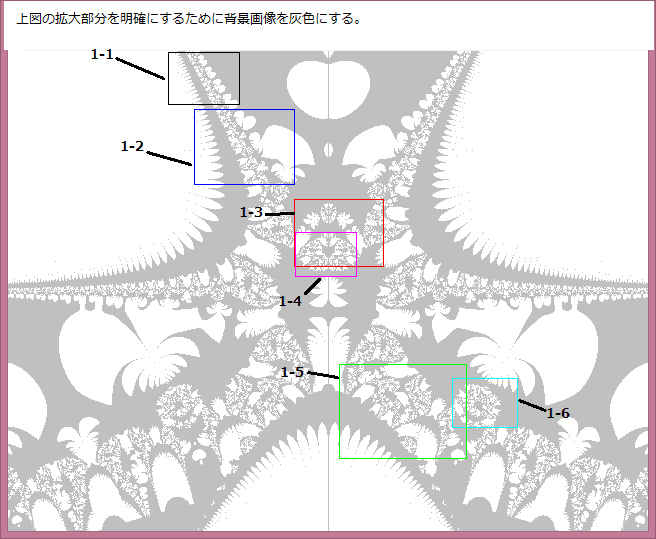
下図は前記事648の1-2-8部分及び1-2-9部分の画像であるが、これら画像にはキズのような小さな黒っぽいモノが見える。これは何だろうか。

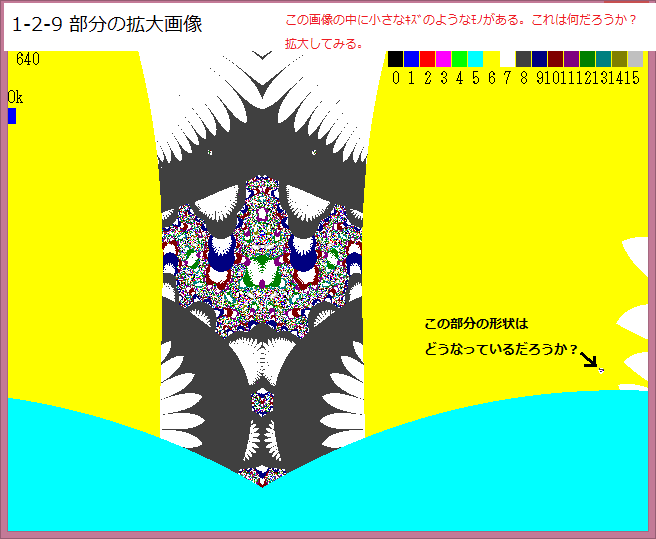
上図のキズのような小さな黒っぽいモノの部分を拡大してみよう。

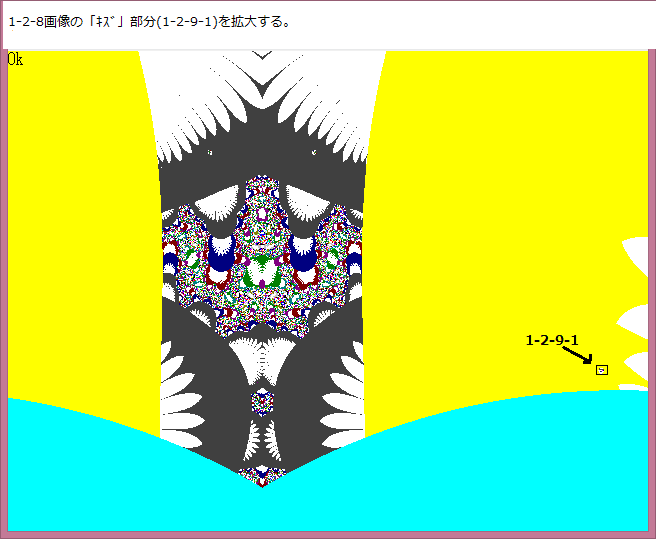
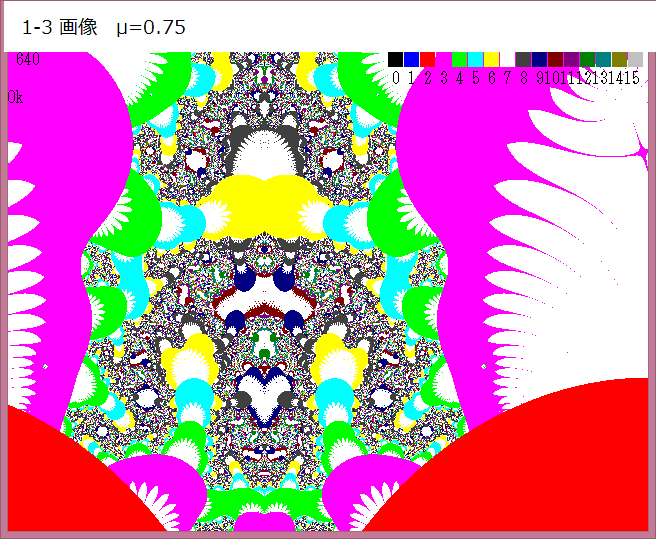
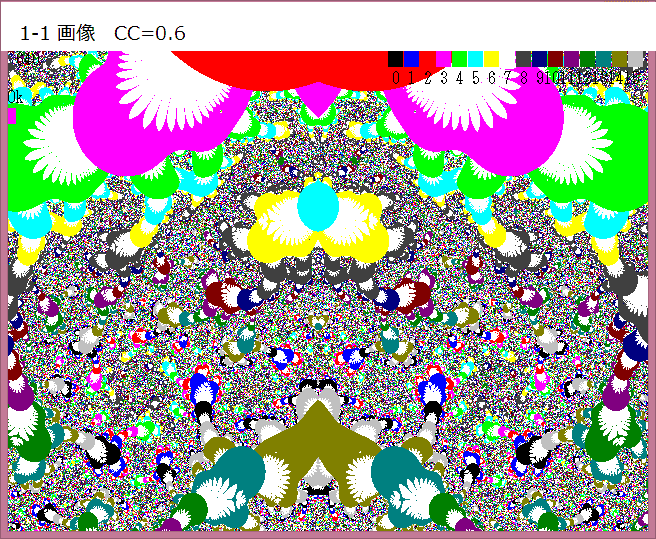
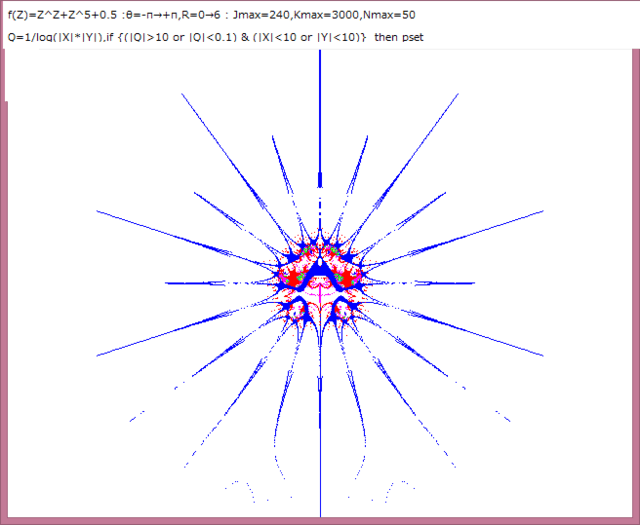
以下が拡大画像である。


------------

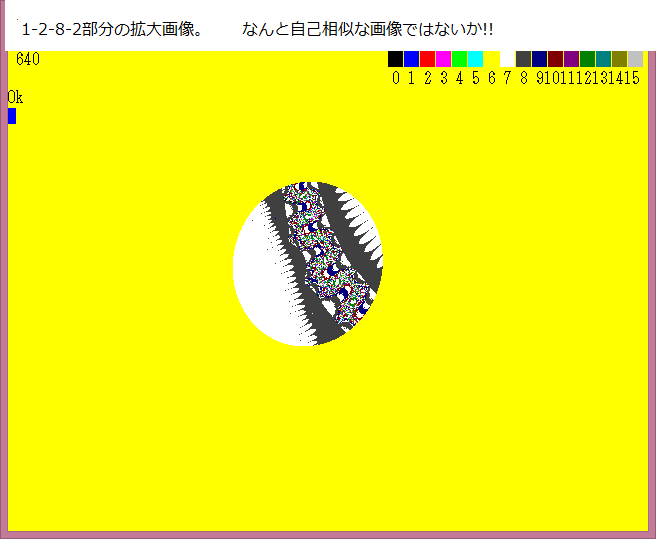
なんと、小さなキズのように見えた部分は上図のような丸い自己相似図形であった!!
こんなところにも自己相似図形が存在しているとは!!と私は驚いている。


上図のキズのような小さな黒っぽいモノの部分を拡大してみよう。


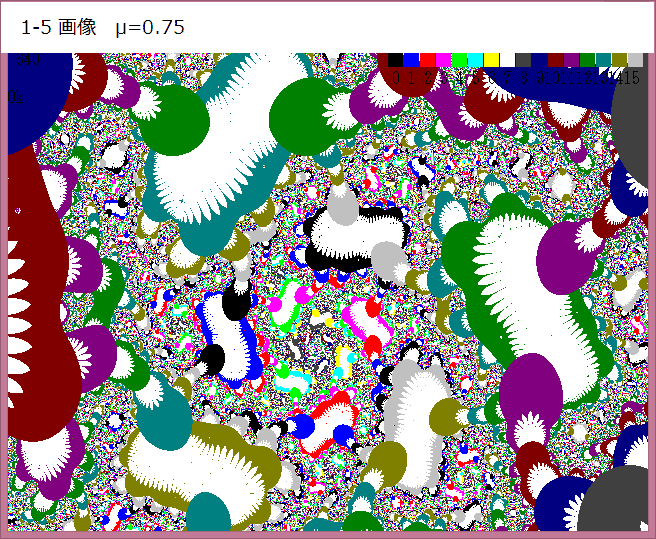
以下が拡大画像である。



------------

なんと、小さなキズのように見えた部分は上図のような丸い自己相似図形であった!!
こんなところにも自己相似図形が存在しているとは!!と私は驚いている。