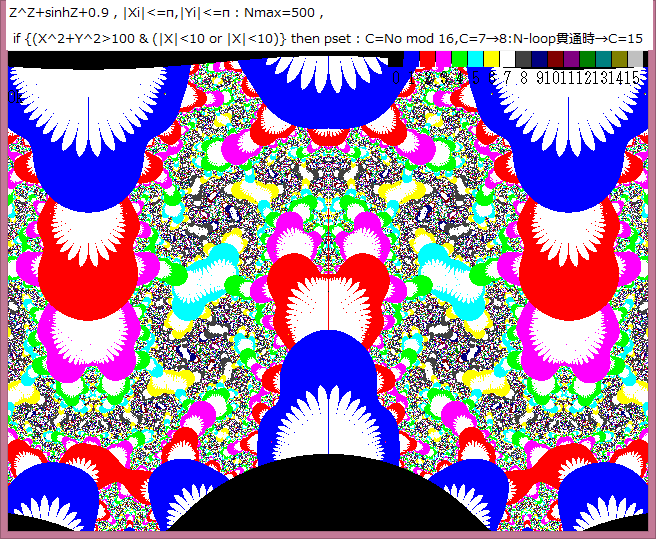
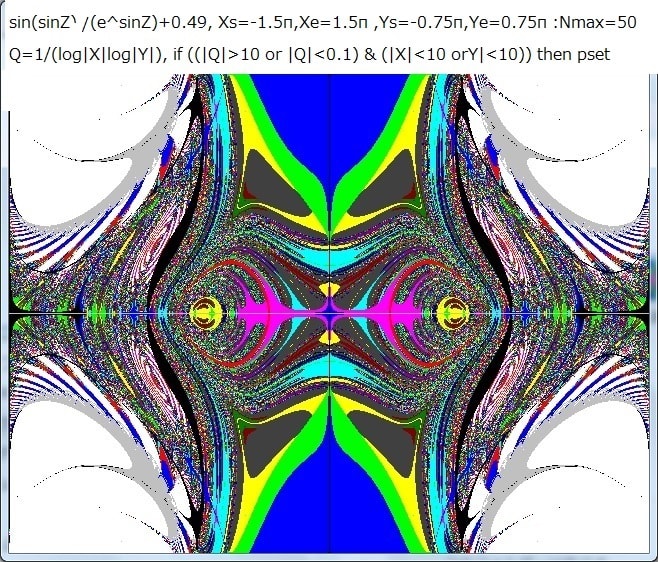
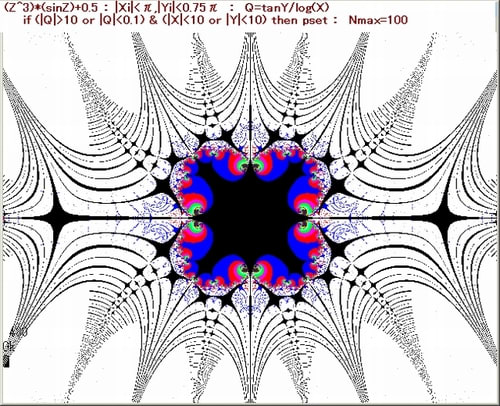
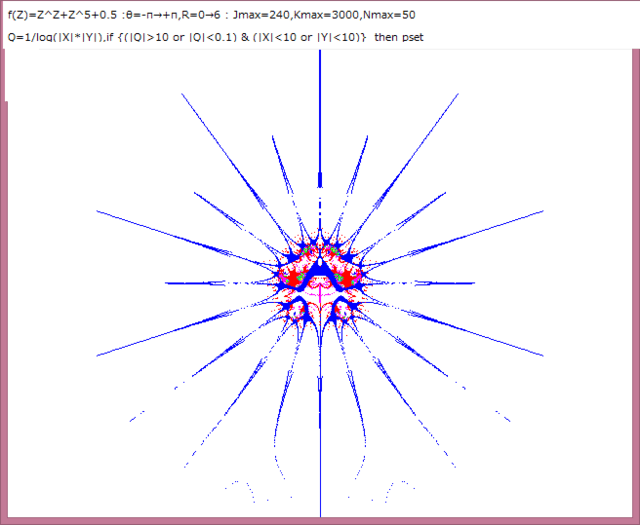
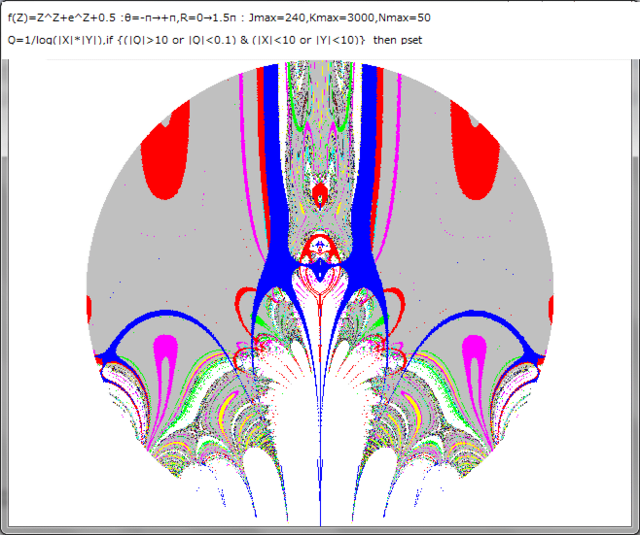
Z^Z+sinhZ+0.7画像の中の部分の拡大画像を求める。
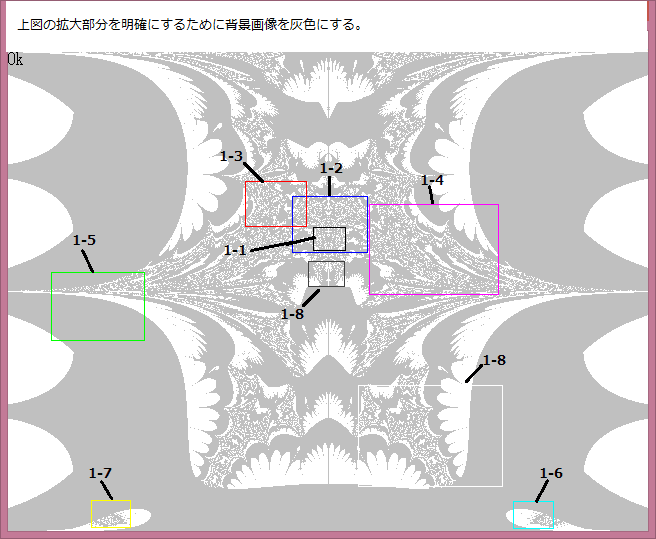
先ず拡大部分を以下に示す。


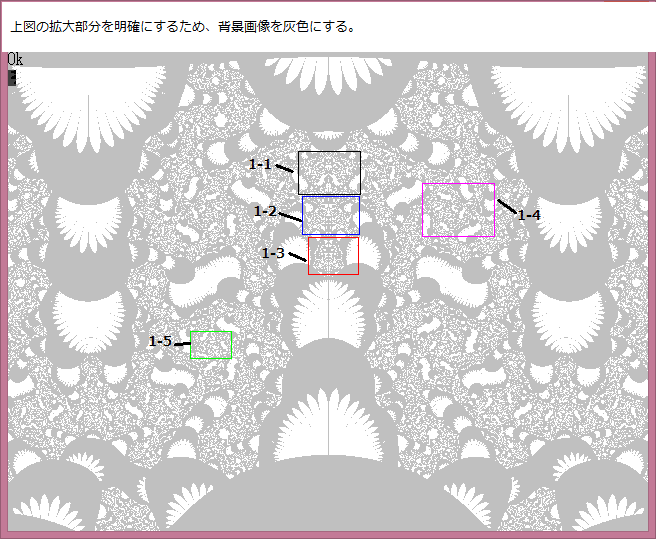
上図の、1-1画像~1-5画像 を以下に示す。


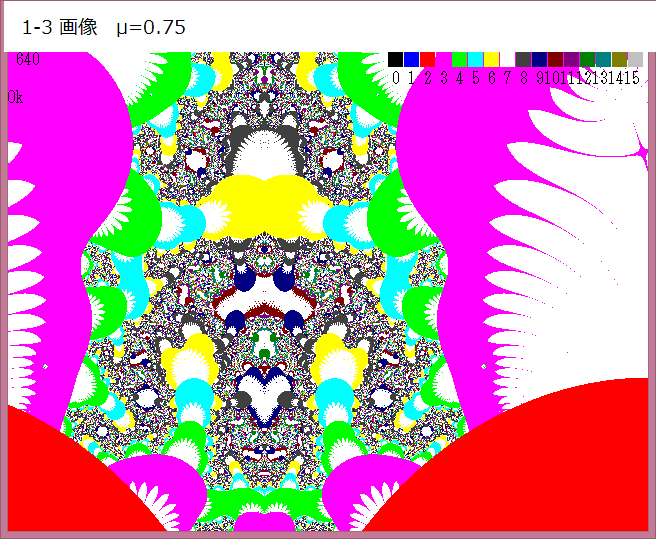

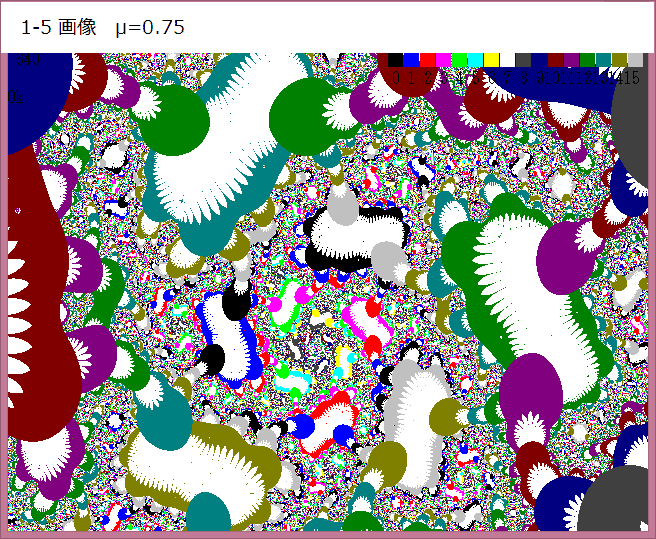
上図の拡大画像において、記事646のような「個性的」な画像は得られなかった。
勿論、「個性的な画像」と言っても主観的なものであり又選んだ複素関数も意図したものではなく偶然に「個性的」な画像になっただけのことであるが、Z^Z+sinhZ+μ画像には残念ながら無かった。
一応、画像作成条件を書いておく。
1.複素関数:Z^Z+sinhZ+0.7
2.画像表示範囲(N-loop入力範囲):|Xi|<=π,|Yi|<=0.75π
3.N-loop脱出条件:(X^2+Y^2)>100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件:(|X|<100 or |Y|<100) ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。
-----------------------------
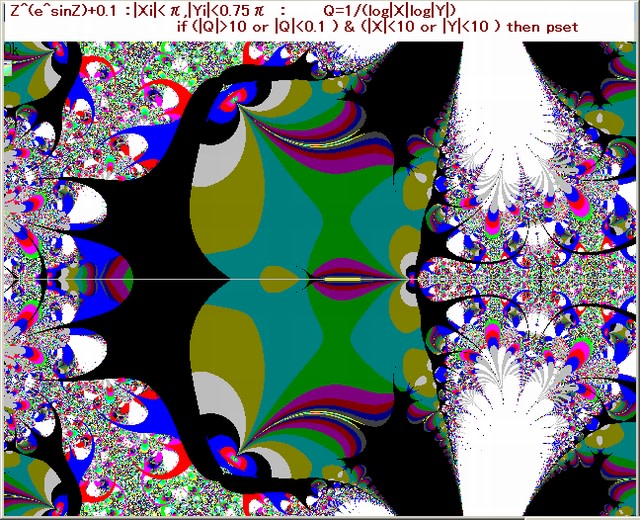
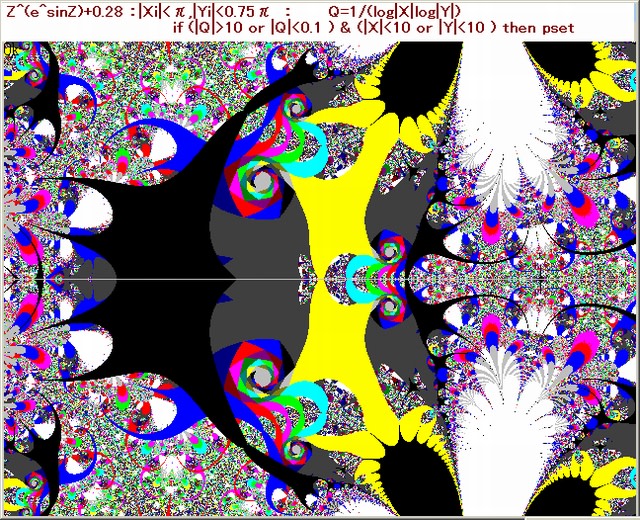
参考のために、0.7→0.6及び0.9 にした場合の画像も添付しておく。
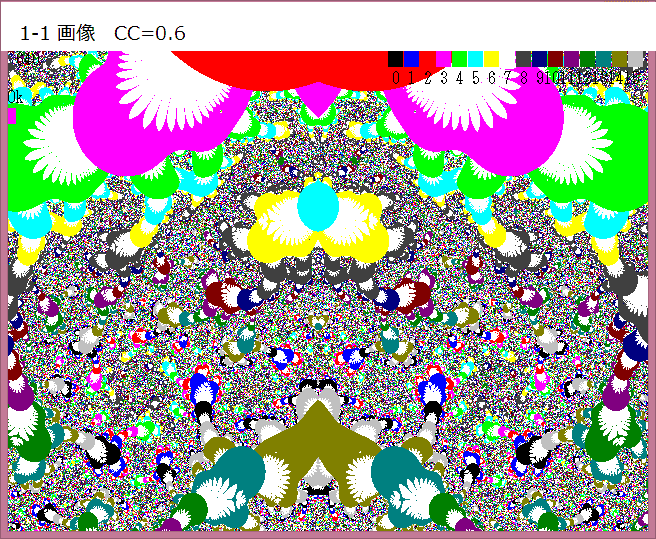

----------------------

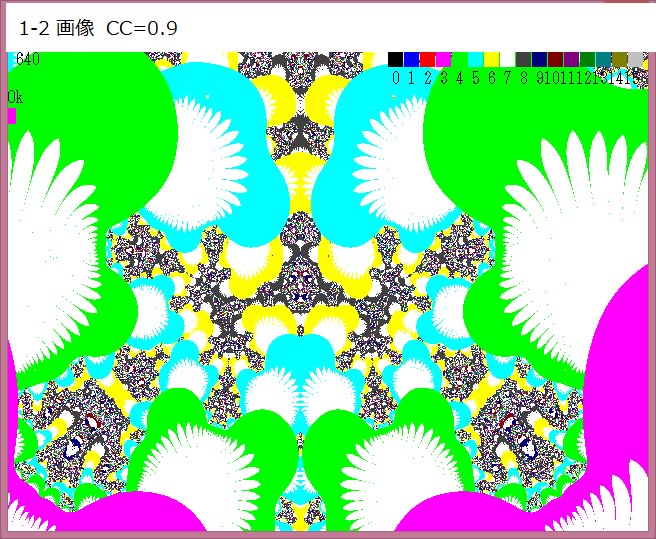
-----------------------
この最後の画像、1-1画像:CC=0.9画像が面白そうなので次記事で調べる。
先ず拡大部分を以下に示す。



上図の、1-1画像~1-5画像 を以下に示す。





上図の拡大画像において、記事646のような「個性的」な画像は得られなかった。
勿論、「個性的な画像」と言っても主観的なものであり又選んだ複素関数も意図したものではなく偶然に「個性的」な画像になっただけのことであるが、Z^Z+sinhZ+μ画像には残念ながら無かった。
一応、画像作成条件を書いておく。
1.複素関数:Z^Z+sinhZ+0.7
2.画像表示範囲(N-loop入力範囲):|Xi|<=π,|Yi|<=0.75π
3.N-loop脱出条件:(X^2+Y^2)>100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件:(|X|<100 or |Y|<100) ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。
-----------------------------
参考のために、0.7→0.6及び0.9 にした場合の画像も添付しておく。


----------------------


-----------------------
この最後の画像、1-1画像:CC=0.9画像が面白そうなので次記事で調べる。