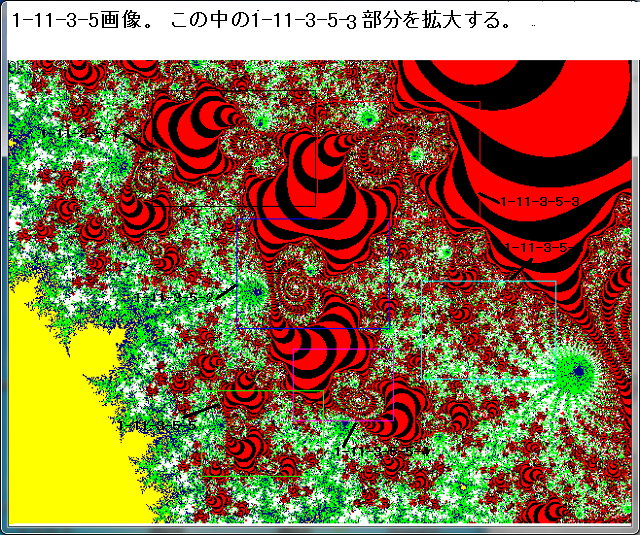
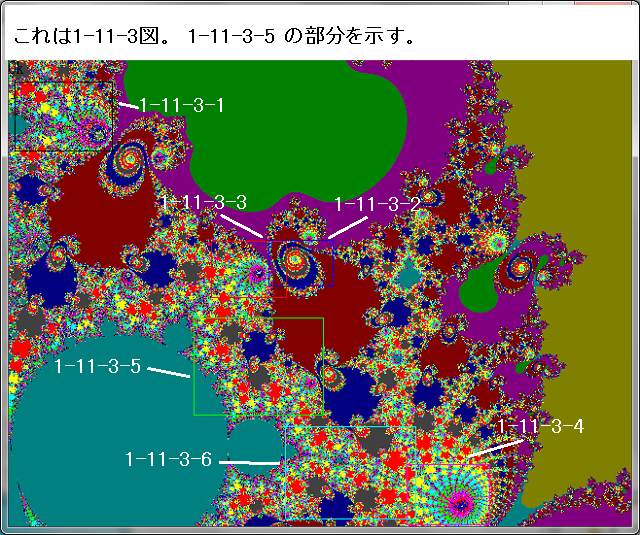
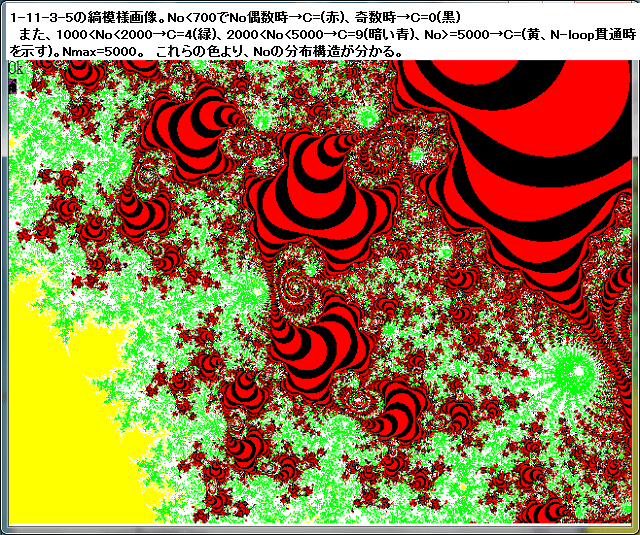
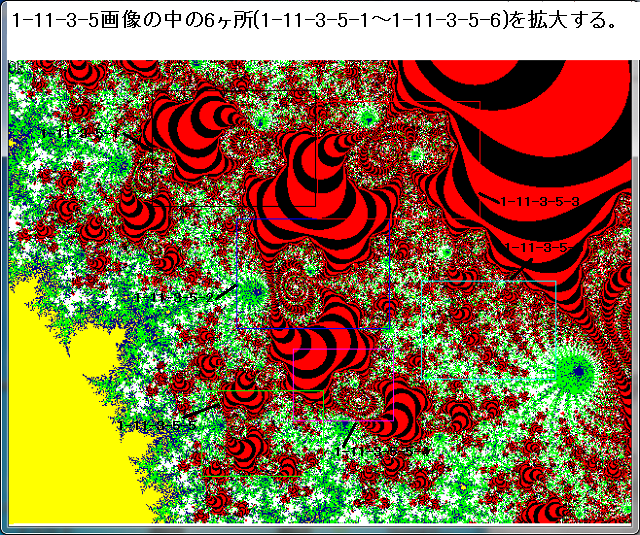
複素関数f(Z)において、nを0を含む自然数とするとき、循環点列
Z(n+1)←f(Zn),n=0,1,2,4,・・・を考える。
複素平面において、始点をZ0から始め、|Zn|>2となったき、複素平面に点Znをpsetする。
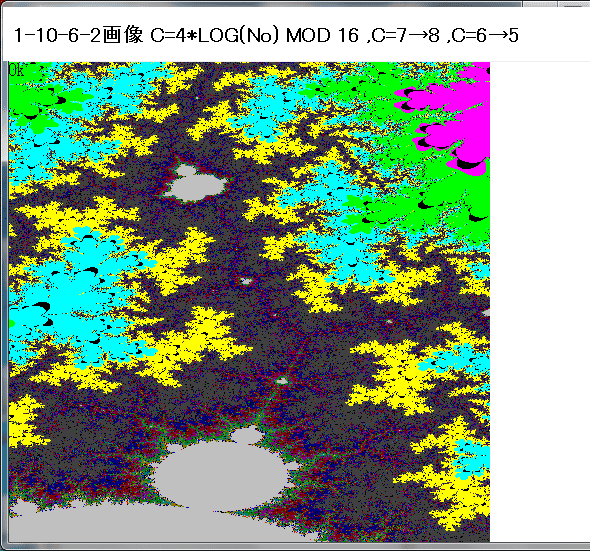
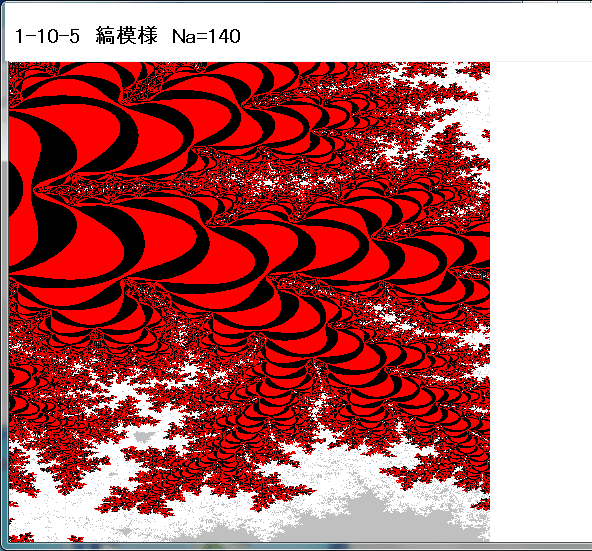
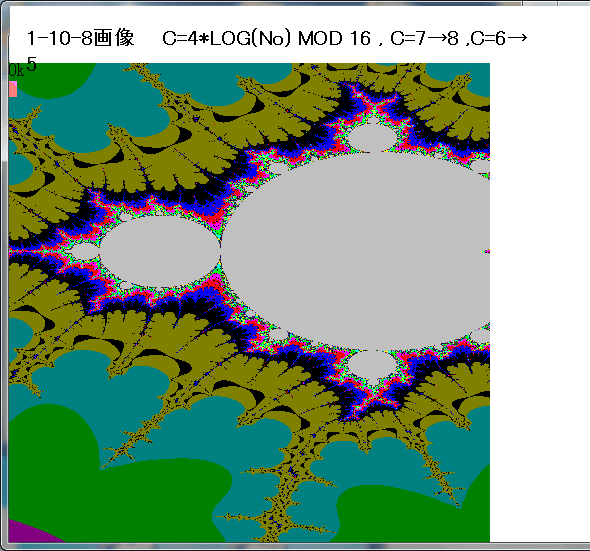
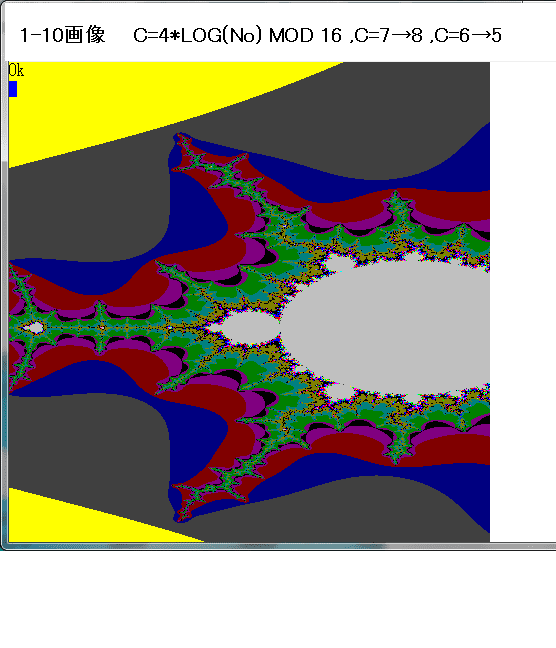
N-maxにおいても|Zn|>2とならない(即ち、N-loop貫通時。収束時。)の点Znの集合をジュリア集合と、ここでは名付ける。以下の画像は、f(Z)=Z^2-1の場合の画像である。
***
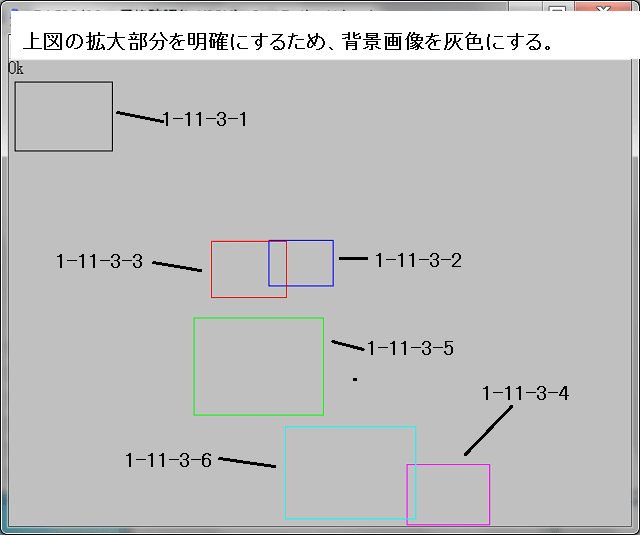
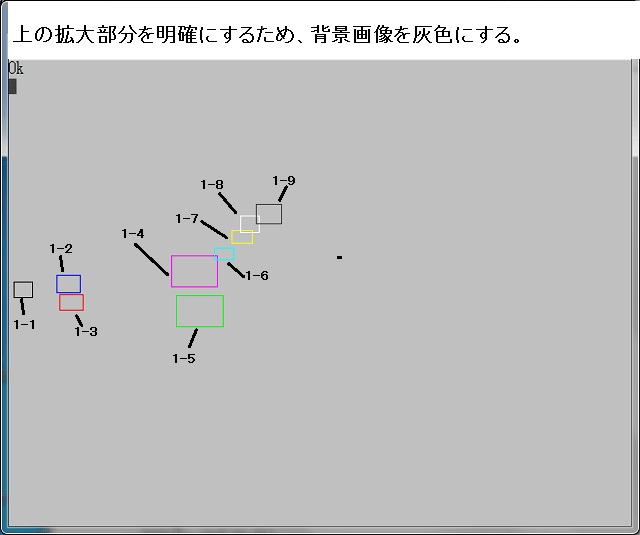
各画像の左上に表示した色コードより、Noの値はジュリア集合部(黄色)に近づくにつれて、1ずつ増加していることが分かる。BASIC/98は16色しか使用できないので、16進で増加していることになる。
--------------------------------------------
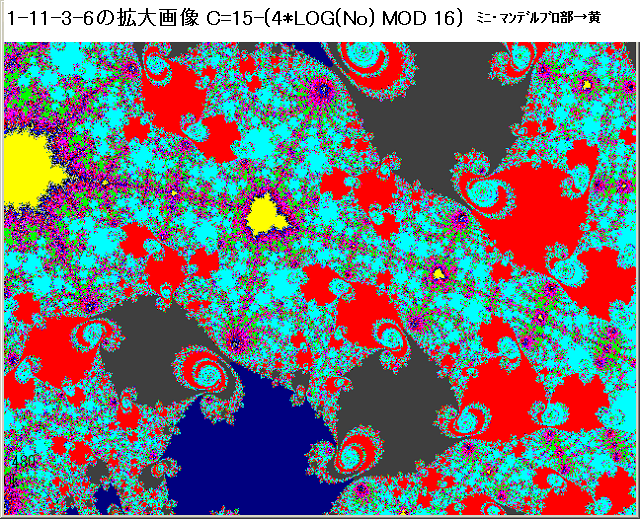
下図の黄色の部分がジュリィア集合である。この画像のBASIC/98のプログラムを最後に書いておく。

---------------------------------------------

--------------------------------------------









------------------------------------------------------------
一番上の画像(Z^2-1のジュリニア集合画像のBASIC/98のプログラム。
5 REM Z^2-1 ジュリニア集合
10 REM Xの範囲を与え、XDOT:YDOT=640:480,DY=DX=(XMAX-XMIN)/XDOT
20 REM OPEN,WRITE 含む
30 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",31,ALL
31 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",32,ALL
32 ON ERROR GOTO 50000
40 CONSOLE ,,0,1
50 COLOR 0,7,,,2
60 CLS 3
70 GOSUB 10000
80 OPEN "C:\BASIC\RUN\DATA.DAT" FOR OUTPUT AS #1
81 OPEN "C:\BASIC\RUN\親DATA.DAT" FOR OUTPUT AS #2
90 REM Xの範囲を与えてYは自動設定
110 XMIN=-1.6 :XMAX=1.6
120 REM X,Yのdot数
130 XDOT=640:YDOT=INT(XDOT*480/640)
140 REM X,Yの実行ステップ幅
150 DX=(XMAX-XMIN)/XDOT :DY=DX
151 YMIN=-DY*YDOT/2:YMAX=-YMIN
152 WRITE #2,XMIN,XMAX,YMIN,YMAX,DX,DY
160 FOR J=0 TO YDOT
170 FOR K=0 TO XDOT
180 X=XMIN+DX*K
190 Y=YMIN+DY*J
200 FOR N=0 TO 50
210 X1=X
220 X=FNR2(X,Y)-1
230 Y=FNI2(X1,Y)
240 REM 発散条件
250 Q=X^2+Y^2
260 IF Q>4 THEN 290 ELSE 270
270 NEXT N
280 C=6 :GOTO 330
290 REM 発散した時点での点(X,Y)のpset条件
310 C=N MOD 16
320 IF C=7 THEN C=8
321 IF C=6 THEN C=5
330 PSET(K,J),C
340 WRITE #1,K,J,C,N
350 NEXT K
360 NEXT J
370 CLOSE
380 END
Z(n+1)←f(Zn),n=0,1,2,4,・・・を考える。
複素平面において、始点をZ0から始め、|Zn|>2となったき、複素平面に点Znをpsetする。
N-maxにおいても|Zn|>2とならない(即ち、N-loop貫通時。収束時。)の点Znの集合をジュリア集合と、ここでは名付ける。以下の画像は、f(Z)=Z^2-1の場合の画像である。
***
各画像の左上に表示した色コードより、Noの値はジュリア集合部(黄色)に近づくにつれて、1ずつ増加していることが分かる。BASIC/98は16色しか使用できないので、16進で増加していることになる。
--------------------------------------------
下図の黄色の部分がジュリィア集合である。この画像のBASIC/98のプログラムを最後に書いておく。

---------------------------------------------


--------------------------------------------









------------------------------------------------------------
一番上の画像(Z^2-1のジュリニア集合画像のBASIC/98のプログラム。
5 REM Z^2-1 ジュリニア集合
10 REM Xの範囲を与え、XDOT:YDOT=640:480,DY=DX=(XMAX-XMIN)/XDOT
20 REM OPEN,WRITE 含む
30 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",31,ALL
31 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",32,ALL
32 ON ERROR GOTO 50000
40 CONSOLE ,,0,1
50 COLOR 0,7,,,2
60 CLS 3
70 GOSUB 10000
80 OPEN "C:\BASIC\RUN\DATA.DAT" FOR OUTPUT AS #1
81 OPEN "C:\BASIC\RUN\親DATA.DAT" FOR OUTPUT AS #2
90 REM Xの範囲を与えてYは自動設定
110 XMIN=-1.6 :XMAX=1.6
120 REM X,Yのdot数
130 XDOT=640:YDOT=INT(XDOT*480/640)
140 REM X,Yの実行ステップ幅
150 DX=(XMAX-XMIN)/XDOT :DY=DX
151 YMIN=-DY*YDOT/2:YMAX=-YMIN
152 WRITE #2,XMIN,XMAX,YMIN,YMAX,DX,DY
160 FOR J=0 TO YDOT
170 FOR K=0 TO XDOT
180 X=XMIN+DX*K
190 Y=YMIN+DY*J
200 FOR N=0 TO 50
210 X1=X
220 X=FNR2(X,Y)-1
230 Y=FNI2(X1,Y)
240 REM 発散条件
250 Q=X^2+Y^2
260 IF Q>4 THEN 290 ELSE 270
270 NEXT N
280 C=6 :GOTO 330
290 REM 発散した時点での点(X,Y)のpset条件
310 C=N MOD 16
320 IF C=7 THEN C=8
321 IF C=6 THEN C=5
330 PSET(K,J),C
340 WRITE #1,K,J,C,N
350 NEXT K
360 NEXT J
370 CLOSE
380 END