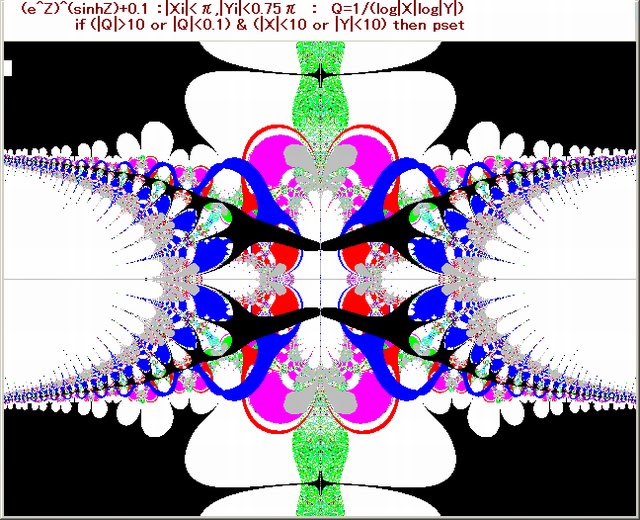
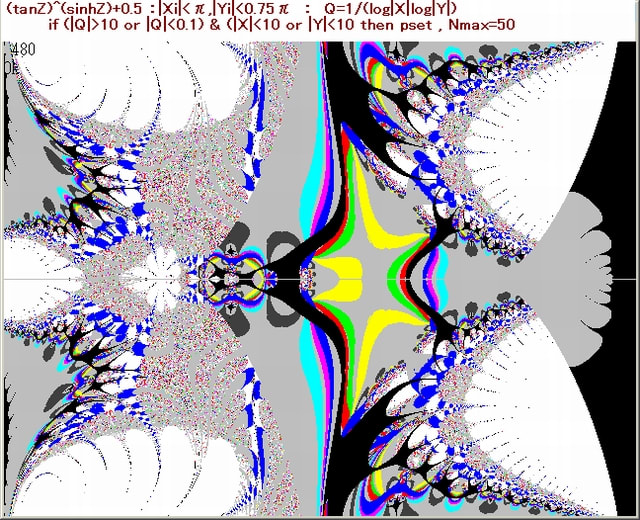
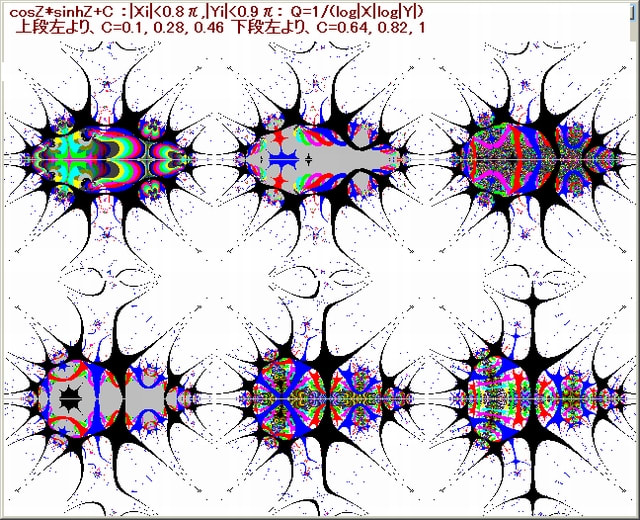
前記事652の、1-9画像の中の4箇所の部分を更に拡大する。
下図が其の1-9画像である。

上図の中の4箇所の部分を下図のように指定する。


上図の4箇所の各拡大画像を以下に示す。




----------------------------------
上図の拡大図から分かるように、同心円状画像の先端から『噴煙』に似たモノが存在している。このような画像構造は此のブログの他の画像でも見られる画像構造であるが、この画像構造については、記事010 『cosZと言う名の噴火連山』において詳しく調べている。
その結果、この画像構造については以下のことが分かっているから其れを引用しておく。
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
『“噴火点”近くの画像は、その画像の大きさ(スケール)を変えても、画像は変わらない。
つまり噴火点近くの画像はフラクタルな画像となっていて、おそらく、この噴火点近くの画像は、N-loopのNmaxを、随時、大きくしていけば、永遠に自己相似な画像が続いていくと思われる。
画像の色から分かるように“噴火点”に接近するにつれて、N-loopを脱出するに必要なN値が1ずつ増加している。(其れは各図の右上に示した色コードから分かる)
従って、『噴火点そのものは、N-loopを脱出するためのN値が無限大となるような、複素平面の特異点である』
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++
以下は補足説明である。
記事652の元図:(sinZ)(e^sinZ)+1を1代目画像とすれば、1-9画像は2代目画像に相当とし、1-9-1~1-9-4は3代目画像に相当する。
記事652の1代目画像は下図である。
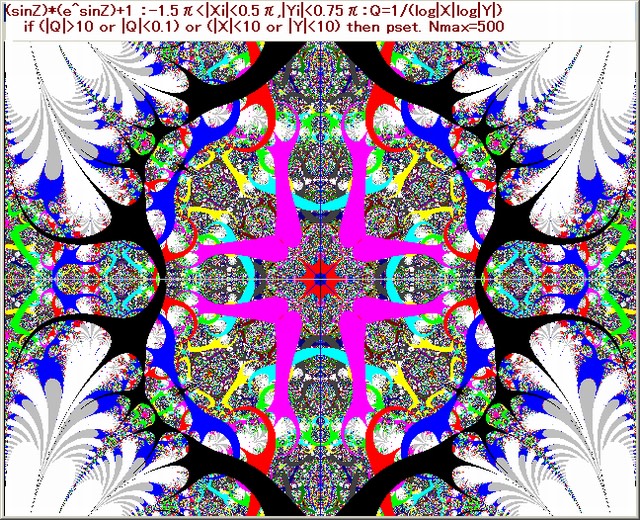
下図に示すように、2代目画像は、1-1~1-10まであり、1-9画像は其の一つである。


-----------------------------------

-----------------------------------
記事652の元図:(sinZ)(e^sinZ)+1を1代目画像の作成条件は以下のとおり。
1. 複素関数:(sinZ)(e^sinZ)+1 。
2. N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>10 or |Q|<0.1)
3. pset条件:|X|<10 or |Y|<10
4. 色設定:N-loop貫通時はC=15。N-loop脱出時は其の時のNをNoとすると C=No mod 16,C=7→8
5. Nmax=500
6. N-loop入力範囲は、-1.5π<Xi<0.5π,|Yi|<0.75π
注:(sinZ)(e^sinZ)+0.64の場合の拡大画像は記事131参照。