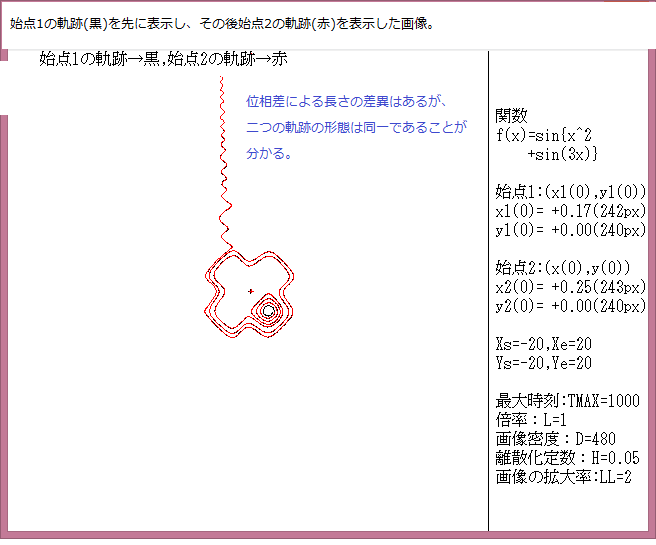
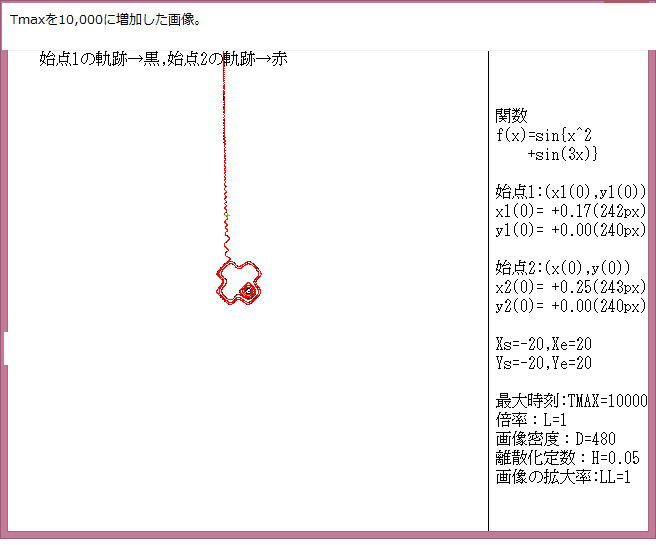
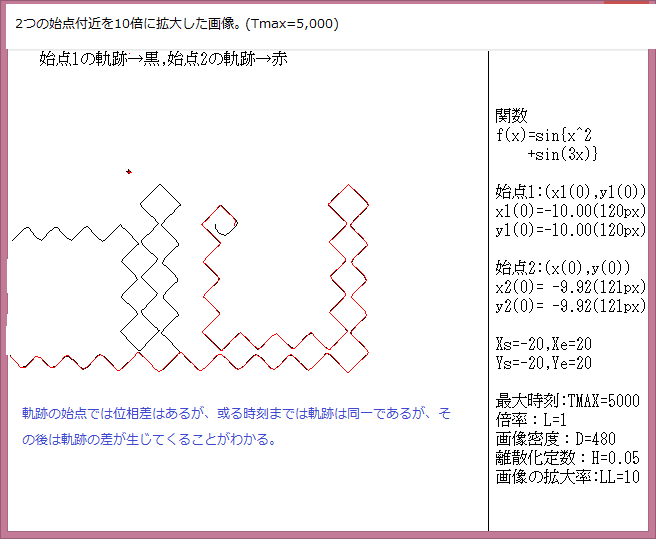
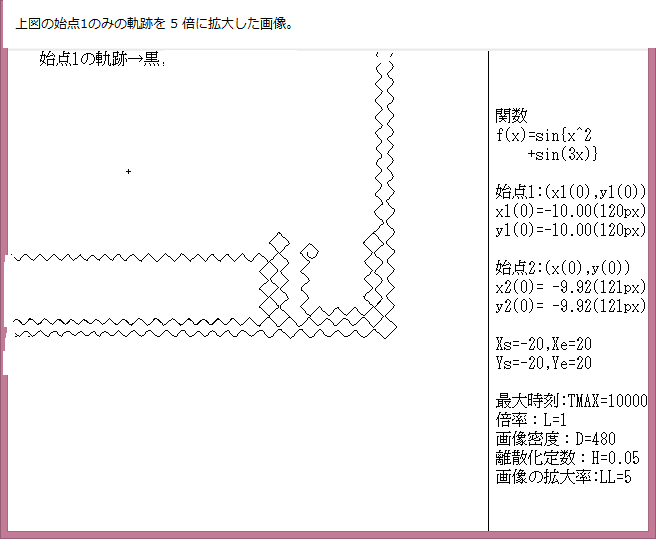
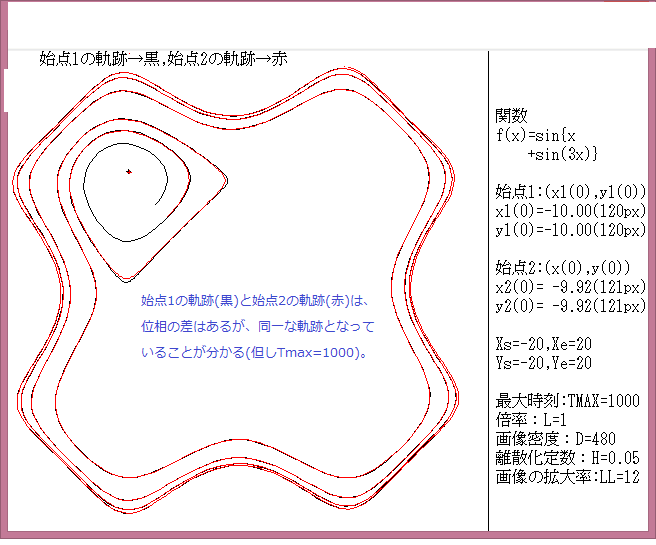
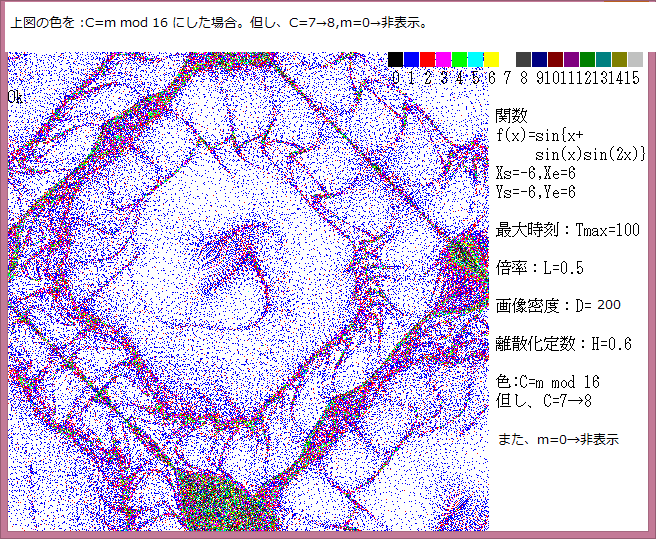
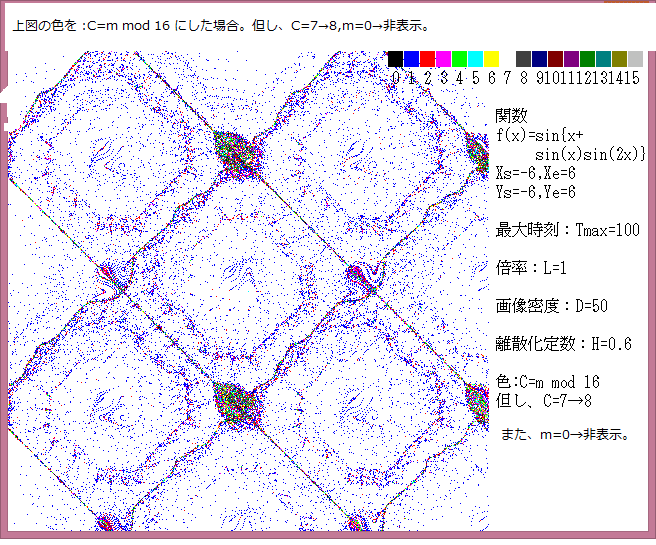
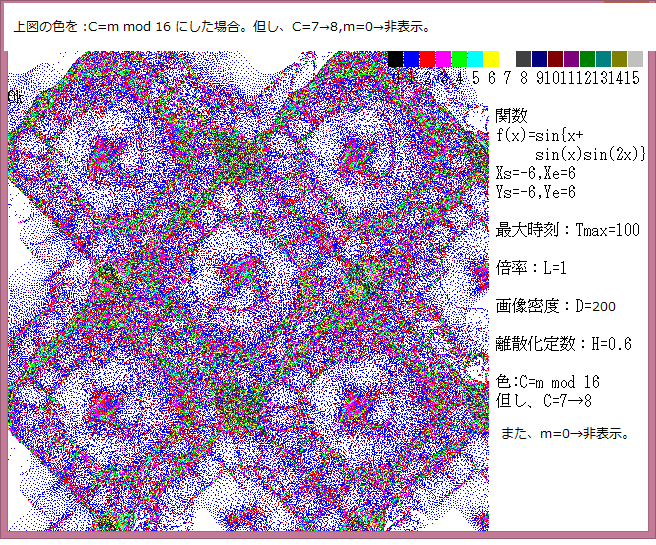
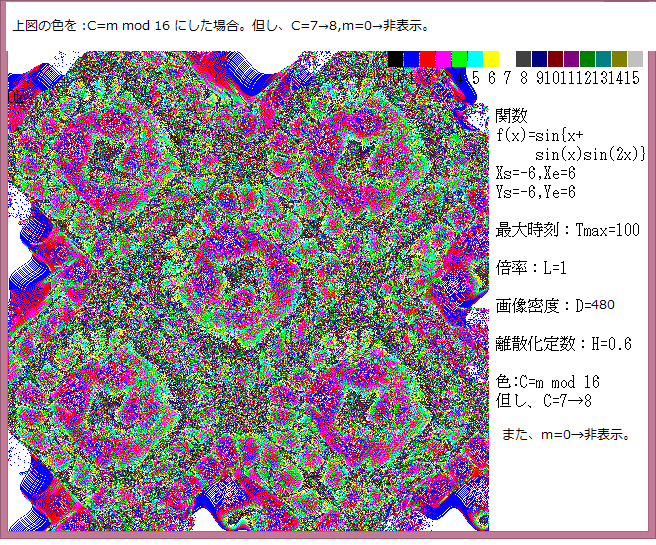
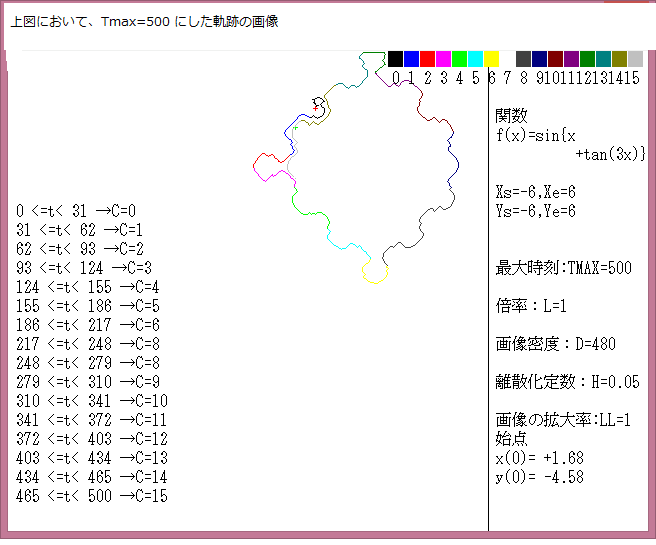
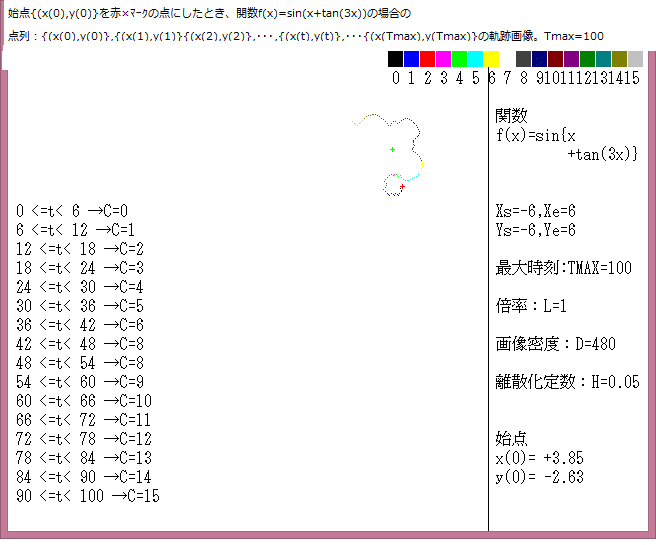
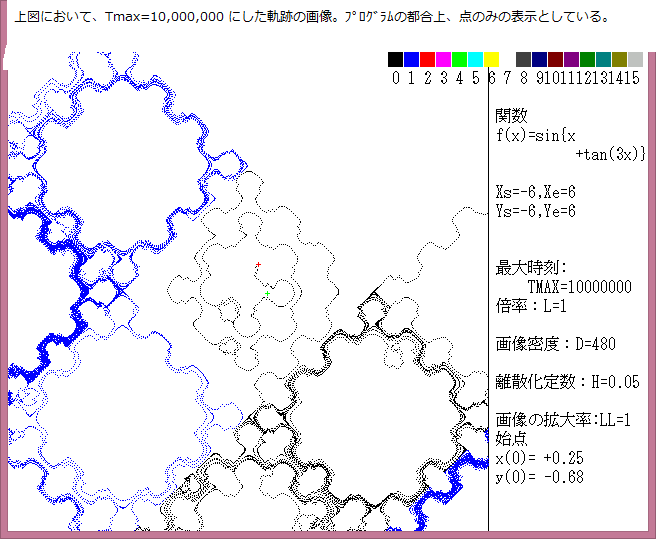
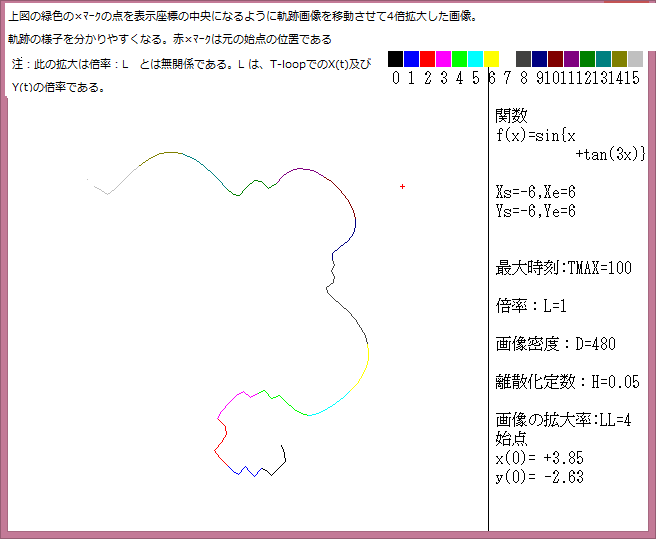
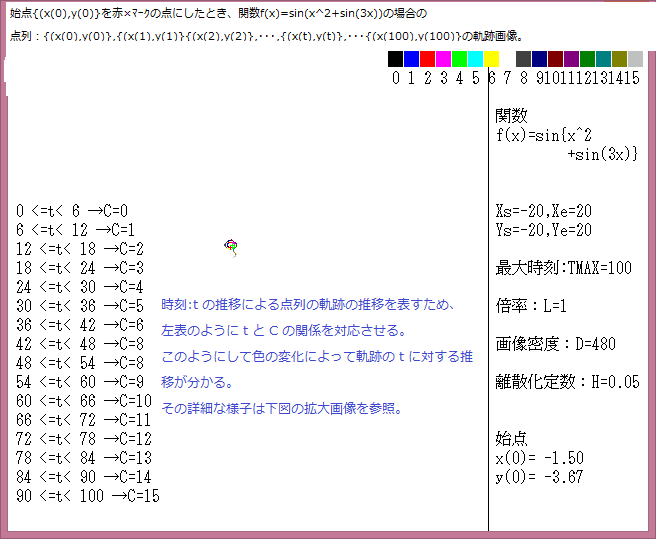
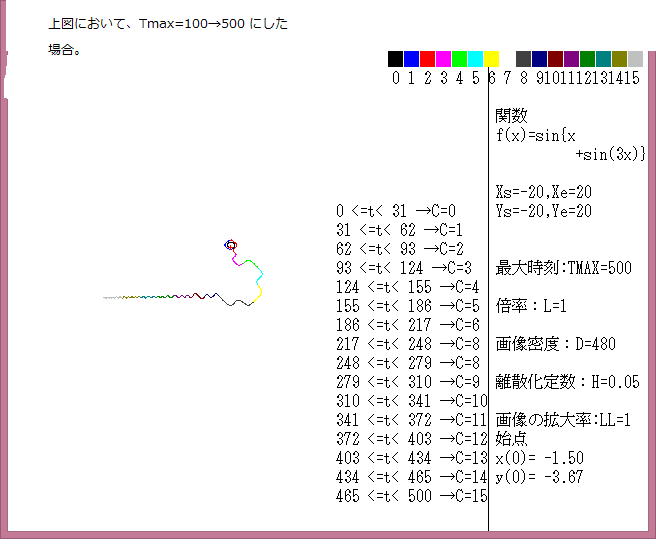
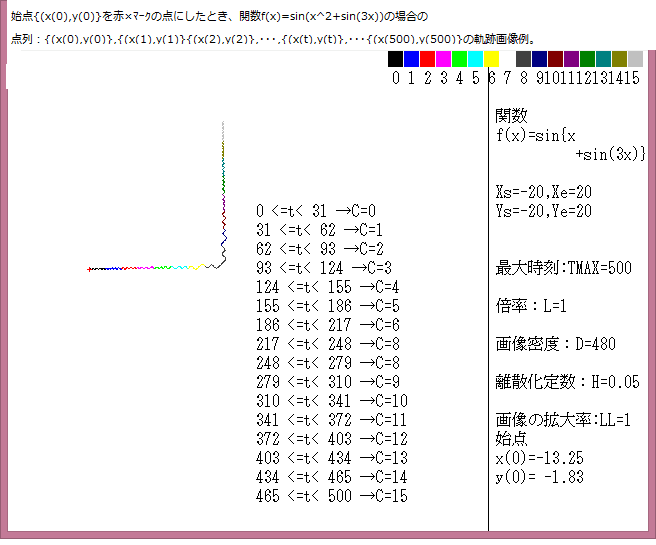
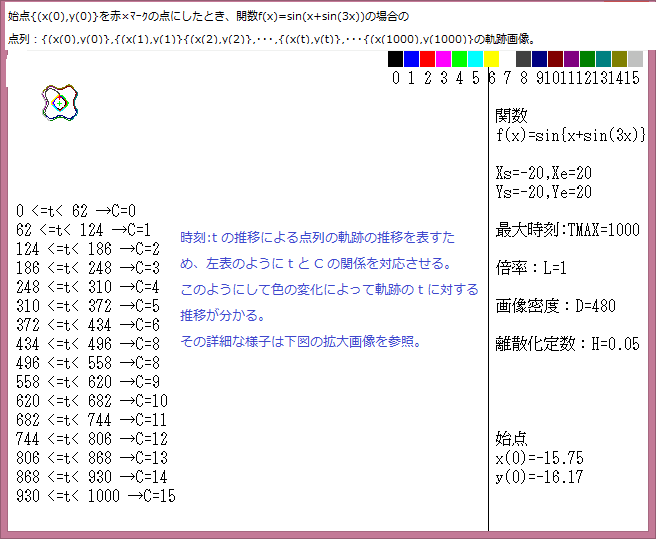
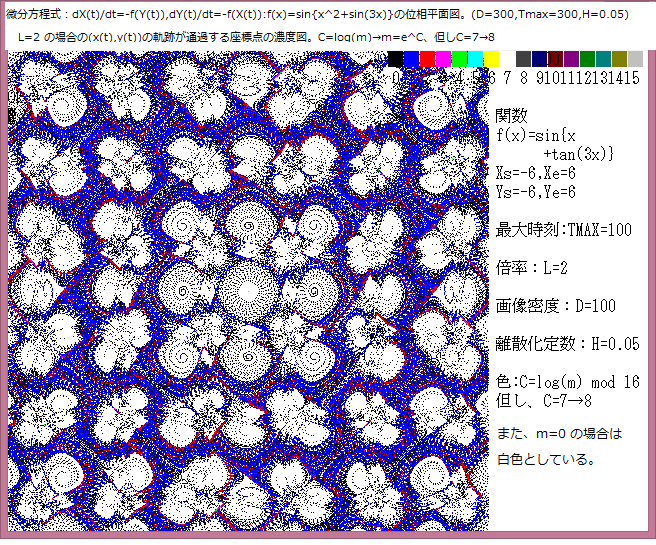
力学サイクル系離散的時間位相平面については、記事541に解説しているが、今回は始点をマウスで与えたときの軌跡について調べる。
マウスで与えた始点は赤色の×で示し、軌跡の変化は色で表示している。具体的な説明は下図に書いてある。
今回の画像は点列:{(x(0),y(0)},{(x(1),y(1)}{(x(2),y(2)},・・・,{(x(t),y(t)},・・・{(x(Tmax),y(Tmax)}において、Tmax=1000としている。
この記事の最後に画像作成のBASIC/98のプログラムを書いておく。
-----------------------------------------------
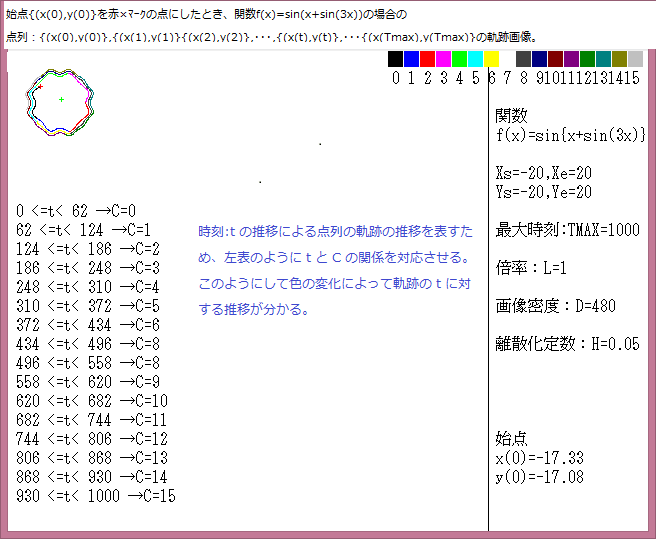

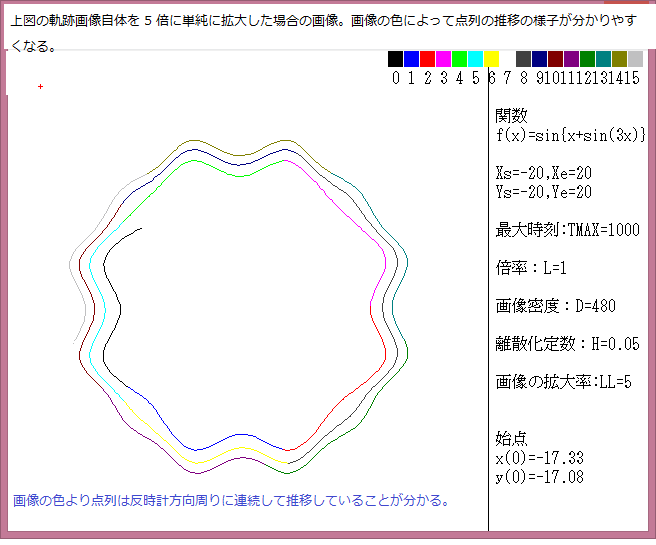
---------------------------------------------------------
画像作成のBASIC/98のプログラム。
1.始点をマウスで与え軌跡画像を求める。また、画像を中央に移動させるための
位置を求めてそのデータを出力する。始点データも出力する。
10 REM 力学系 始点及をマウスで与えて軌跡の表示する。また画像のbias点(C,D)を求める。
20 REM 始点のマウス入力はマウスの左ボタンをクリック。
30 REM parameter→行320
40 REM 横軸(K):480 dots、縦軸(J):480 dots
50 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",60,ALL
60 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER1.BAS",70,ALL
70 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR右上表示.BAS",80,ALL
80 ON ERROR GOTO 50000
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
120 GOSUB 10000
130 LINE (480,0)-(480,480),0
140 LOCATE 61,3:PRINT "関数"
150 LOCATE 61,4:PRINT "f(x)=sin{x+sin(3x)}"
160 LOCATE 61,6:PRINT "Xs=-20,Xe=20"
170 LOCATE 61,7:PRINT "Ys=-20,Ye=20"
180 LOCATE 61,9:PRINT "最大時刻:TMAX=1000"
190 LOCATE 61,11:PRINT "倍率:L=1"
200 LOCATE 61,13:PRINT "画像密度:D=480"
210 LOCATE 61,15:PRINT "離散化定数:H=0.05"
220 '
230 '
240 OPEN "C:\BASIC1\RUN\軌跡DATA1.DAT" FOR OUTPUT AS #1
250 OPEN "C:\BASIC1\RUN\始点DATA1.DAT" FOR OUTPUT AS #2
260 ON MOUSE(2) GOSUB *M1
270 MOUSE (2) ON
280 DO:AA=AA:LOOP
290 *M1
300 A=MOUSE(4,1):B=MOUSE(5,1)
310 '
320 XS=-20:XE=20:YS=-20:YE=20:H=0.05:D=480:L=1:TMAX=1000:V=0
330 DX=(XE-XS)/D:DY=(YE-YS)/D:TT=TMAX/16:T1=INT(TT)
340 JJ=B
350 '
360 YY=YS+DY*JJ:Y0=YY
370 KK=A
380 XX=XS+DX*KK:X0=XX
390 FOR T=0 TO TMAX
400 X=XX:Y=YY
410 XX=X-H*SIN(Y+SIN(3*Y))
420 YY=Y+H*SIN(X+SIN(3*X))
430 XXX=L*XX:YYY=L*YY
440 J=12*YYY+240
450 K=12*XXX+240
460 IF J<0 OR J>480 THEN 540
470 IF K<0 OR K>480 THEN 540
480 '
490 '
500 '
510 GOSUB 830
520 PSET (K,J),CC
530 WRITE #1,K,J,CC
540 NEXT T
550 YY=Y1
560 PSET (A,B),2
570 PSET (A+1,B),2
580 PSET (A+2,B),2
590 PSET (A-1,B),2
600 PSET (A-2,B),2
610 PSET (A,B+1),2
620 PSET (A,B+2),2
630 PSET (A,B-1),2
640 PSET (A,B-2),2
650 LOCATE 61,20:PRINT "始点"
660 LOCATE 61,21:PRINT "x(0)=":LOCATE 66,21:PRINT USING "+##.##";X0
670 LOCATE 61,22:PRINT "y(0)=":LOCATE 66,22:PRINT USING "+##.##";Y0
680 WRITE #2,A,B,X0,Y0
690 GOSUB 3000
691 GOTO 730
710 INPUT "画像のbias点を求めるか(求める)→1";A1
720 IF A1=1 THEN 730 ELSE 810
730 REM 画像のbias点(C,D)を左クリックで求め、BIAS*.DATに出力する。
740 OPEN "C:\BASIC1\RUN\BIAS1.DAT" FOR OUTPUT AS #3
750 ON MOUSE(2) GOSUB *M2
760 MOUSE (2) ON
770 DO:AA=AA:LOOP
780 *M2
790 C=MOUSE(4,1):D=MOUSE(5,1)
800 WRITE #3,C,D
801 PSET (C,D),4
802 PSET (C+1,D),4
803 PSET (C+2,D),4
804 PSET (C-1,D),4
805 PSET (C-2,D),4
806 PSET (C,D+1),4
807 PSET (C,D+2),4
808 PSET (C,D-1),4
809 PSET (C,D-2),4
810 GOSUB 1010
820 CLOSE:LOCATE 0,0:END
830 REM 時刻の色
840 IF T>=0 AND T
=TT AND T<2*TT THEN CC=1:GOTO 1000
860 IF T>=2*TT AND T<3*TT THEN CC=2:GOTO 1000
870 IF T>=3*TT AND T<4*TT THEN CC=3:GOTO 1000
880 IF T>=4*TT AND T<5*TT THEN CC=4:GOTO 1000
890 IF T>=5*TT AND T<6*TT THEN CC=5:GOTO 1000
900 IF T>=6*TT AND T<7*TT THEN CC=6:GOTO 1000
910 IF T>=7*TT AND T<8*TT THEN CC=8:GOTO 1000
920 IF T>=8*TT AND T<9*TT THEN CC=7:GOTO 1000
930 IF T>=9*TT AND T<10*TT THEN CC=9:GOTO 1000
940 IF T>=10*TT AND T<11*TT THEN CC=10:GOTO 1000
950 IF T>=11*TT AND T<12*TT THEN CC=11:GOTO 1000
960 IF T>=12*TT AND T<13*TT THEN CC=12:GOTO 1000
970 IF T>=13*TT AND T<14*TT THEN CC=13:GOTO 1000
980 IF T>=14*TT AND T<15*TT THEN CC=14:GOTO 1000
990 IF T>=15*TT AND T<16*TT THEN CC=15:GOTO 1000
1000 RETURN
1010 REM 時刻の表示
1020 LOCATE V,8:PRINT 0;"<=t<";T1;"→C=0"
1030 LOCATE V,9:PRINT T1;"<=t<";2*T1;"→C=1"
1040 LOCATE V,10:PRINT 2*T1;"<=t<";3*T1;"→C=2"
1050 LOCATE V,11:PRINT 3*T1;"<=t<";4*T1;"→C=3"
1060 LOCATE V,12:PRINT 4*T1;"<=t<";5*T1;"→C=4"
1070 LOCATE V,13:PRINT 5*T1;"<=t<";6*T1;"→C=5"
1080 LOCATE V,14:PRINT 6*T1;"<=t<";7*T1;"→C=6"
1090 LOCATE V,15:PRINT 7*T1;"<=t<";8*T1;"→C=8"
1100 LOCATE V,16:PRINT 8*T1;"<=t<";9*T1;"→C=8"
1110 LOCATE V,17:PRINT 9*T1;"<=t<";10*T1;"→C=9"
1120 LOCATE V,18:PRINT 10*T1;"<=t<";11*T1;"→C=10"
1130 LOCATE V,19:PRINT 11*T1;"<=t<";12*T1;"→C=11"
1140 LOCATE V,20:PRINT 12*T1;"<=t<";13*T1;"→C=12"
1150 LOCATE V,21:PRINT 13*T1;"<=t<";14*T1;"→C=13"
1160 LOCATE V,22:PRINT 14*T1;"<=t<";15*T1;"→C=14"
1170 LOCATE V,23:PRINT 15*T1;"<=t<";TMAX;"→C=15"
1180 RETURN
***
2.始点データ及び画像移動位置データを読み込み、軌跡画像を表示座標の
中央に移動させる。また其の画像を任意に拡大表示させる。
0 REM 力学系 始点及びbias点を読込み軌跡の移動表示する
20 REM 始点データ・ファイル名→始点DATA*.DAT (A,B,XX,YY)
21 REM bias点データ・ファイル名→BIAS*.DAT
30 REM parameter→行310
40 REM 横軸(K):480 dots、縦軸(J):480 dots
50 CHAIN MERGE "C:BASIC1PROSUBRKOSHIKI.BAS",60,ALL
60 CHAIN MERGE "C:BASIC1PROSUBRER1.BAS",70,ALL
70 CHAIN MERGE "C:BASIC1PROSUBRCOLOR右上表示.BAS",80,ALL
80 ON ERROR GOTO 50000
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
120 GOSUB 10000
130 LINE (480,0)-(480,480),0
140 LOCATE 61,3:PRINT "関数"
150 LOCATE 61,4:PRINT "f(x)=sin{x+sin(3x)}"
160 LOCATE 61,6:PRINT "Xs=-20,Xe=20"
170 LOCATE 61,7:PRINT "Ys=-20,Ye=20"
180 LOCATE 61,9:PRINT "最大時刻:TMAX=1000"
190 LOCATE 61,11:PRINT "倍率:L=2"
200 LOCATE 61,13:PRINT "画像密度:D=480"
210 LOCATE 61,15:PRINT "離散化定数:H=0.05"
220 LOCATE 61,17:PRINT "画像の拡大率:LL=3"
230 '
240 OPEN "C:BASIC1RUN軌跡DATA1.DAT" FOR OUTPUT AS #1
241 OPEN "C:BASIC1RUN始点DATA1.DAT" FOR INPUT AS #2
242 INPUT #2,A,B,X0,Y0
300 OPEN "C:BASIC1RUNBIAS1.DAT" FOR INPUT AS #3
301 INPUT #3,C,DA
310 XS=-20:XE=20:YS=-20:YE=20:H=0.05:D=480:L=1:TMAX=1000:V=0:LL=3
320 DX=(XE-XS)/D:DY=(YE-YS)/D:TT=TMAX/16:T1=INT(TT)
330 JJ=B
340 '
350 YY=YS+DY*JJ:Y1=YY
360 KK=A
370 XX=XS+DX*KK
380 FOR T=0 TO TMAX
390 X=XX:Y=YY
400 XX=X-H*SIN(Y+SIN(3*Y))
410 YY=Y+H*SIN(X+SIN(3*X))
420 XXX=L*XX:YYY=L*YY
430 J=12*YYY+240
440 K=12*XXX+240
441 JJ=LL*(J-DA)+240
442 KK=LL*(K-C)+240
450 IF JJ<0 OR JJ>480 THEN 530
460 IF KK<0 OR KK>480 THEN 530
470 '
480 '
490 '
500 GOSUB 670
510 PSET (KK,JJ),CC
520 WRITE #1,KK,JJ,CC
530 NEXT T
540 YY=Y1
550 PSET (A,B),2
560 PSET (A+1,B),2
570 PSET (A+2,B),2
580 PSET (A-1,B),2
590 PSET (A-2,B),2
600 PSET (A,B+1),2
610 PSET (A,B+2),2
620 PSET (A,B-1),2
630 PSET (A,B-2),2
631 LOCATE 61,20:PRINT "始点"
632 LOCATE 61,21:PRINT "x(0)=":LOCATE 66,21:PRINT USING "+##.##";X0
633 LOCATE 61,22:PRINT "y(0)=":LOCATE 66,22:PRINT USING "+##.##";Y0
650 GOSUB 3000
651 GOSUB 850
652 CLOSE
653 LOCATE 0,0
660 END
670 REM 軌跡の色
680 IF T>=0 AND T=TT AND T<2*TT THEN CC=1:GOTO 840
700 IF T>=2*TT AND T<3*TT THEN CC=2:GOTO 840
710 IF T>=3*TT AND T<4*TT THEN CC=3:GOTO 840
720 IF T>=4*TT AND T<5*TT THEN CC=4:GOTO 840
730 IF T>=5*TT AND T<6*TT THEN CC=5:GOTO 840
740 IF T>=6*TT AND T<7*TT THEN CC=6:GOTO 840
750 IF T>=7*TT AND T<8*TT THEN CC=8:GOTO 840
760 IF T>=8*TT AND T<9*TT THEN CC=7:GOTO 840
770 IF T>=9*TT AND T<10*TT THEN CC=9:GOTO 840
780 IF T>=10*TT AND T<11*TT THEN CC=10:GOTO 840
790 IF T>=11*TT AND T<12*TT THEN CC=11:GOTO 840
800 IF T>=12*TT AND T<13*TT THEN CC=12:GOTO 840
810 IF T>=13*TT AND T<14*TT THEN CC=13:GOTO 840
820 IF T>=14*TT AND T<15*TT THEN CC=14:GOTO 840
830 IF T>=15*TT AND T<16*TT THEN CC=15:GOTO 840
840 RETURN
850 REM 時刻の表示
860 LOCATE V,8:PRINT 0;"<=t<";T1;"→C=0"
870 LOCATE V,9:PRINT T1;"<=t<";2*T1;"→C=1"
880 LOCATE V,10:PRINT 2*T1;"<=t<";3*T1;"→C=2"
890 LOCATE V,11:PRINT 3*T1;"<=t<";4*T1;"→C=3"
900 LOCATE V,12:PRINT 4*T1;"<=t<";5*T1;"→C=4"
910 LOCATE V,13:PRINT 5*T1;"<=t<";6*T1;"→C=5"
920 LOCATE V,14:PRINT 6*T1;"<=t<";7*T1;"→C=6"
930 LOCATE V,15:PRINT 7*T1;"<=t<";8*T1;"→C=8"
940 LOCATE V,16:PRINT 8*T1;"<=t<";9*T1;"→C=8"
950 LOCATE V,17:PRINT 9*T1;"<=t<";10*T1;"→C=9"
960 LOCATE V,18:PRINT 10*T1;"<=t<";11*T1;"→C=10"
970 LOCATE V,19:PRINT 11*T1;"<=t<";12*T1;"→C=11"
980 LOCATE V,20:PRINT 12*T1;"<=t<";13*T1;"→C=12"
990 LOCATE V,21:PRINT 13*T1;"<=t<";14*T1;"→C=13"
1000 LOCATE V,22:PRINT 14*T1;"<=t<";15*T1;"→C=14"
1010 LOCATE V,23:PRINT 15*T1;"<=t<";TMAX;"→C=15"
1011 RETURN
***
3.表示座標の中央に移動した軌跡画像を線で表示させる。
10 REM 力学系 始点及びbias点を読込み軌跡の移動表示する→表示を線化
20 REM 始点データ・ファイル名→始点DATA*.DAT (A,B,XX,YY)
21 REM bias点データ・ファイル名→BIAS*.DAT
30 REM parameter→行310
40 REM 横軸(K):480 dots、縦軸(J):480 dots
50 CHAIN MERGE "C:BASIC1PROSUBRKOSHIKI.BAS",60,ALL
60 CHAIN MERGE "C:BASIC1PROSUBRER1.BAS",70,ALL
70 CHAIN MERGE "C:BASIC1PROSUBRCOLOR右上表示.BAS",80,ALL
80 ON ERROR GOTO 50000
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
120 GOSUB 10000
130 LINE (480,0)-(480,480),0
140 LOCATE 61,3:PRINT "関数"
150 LOCATE 61,4:PRINT "f(x)=sin{x+sin(3x)}"
160 LOCATE 61,6:PRINT "Xs=-20,Xe=20"
170 LOCATE 61,7:PRINT "Ys=-20,Ye=20"
180 LOCATE 61,9:PRINT "最大時刻:TMAX=1000"
190 LOCATE 61,11:PRINT "倍率:L=1"
200 LOCATE 61,13:PRINT "画像密度:D=480"
210 LOCATE 61,15:PRINT "離散化定数:H=0.05"
220 LOCATE 61,17:PRINT "画像の拡大率:LL=5"
230 '
240 OPEN "C:BASIC1RUN軌跡DATA1.DAT" FOR OUTPUT AS #1
241 OPEN "C:BASIC1RUN始点DATA1.DAT" FOR INPUT AS #2
242 INPUT #2,A,B,X0,Y0
300 OPEN "C:BASIC1RUNBIAS1.DAT" FOR INPUT AS #3
301 INPUT #3,C,DA
310 XS=-20:XE=20:YS=-20:YE=20:H=0.05:D=480:L=1:TMAX=1000:T1=INT(TMAX/16):V=0:LL=5
320 DX=(XE-XS)/D:DY=(YE-YS)/D:TT=TMAX/16:T1=INT(TT)
330 JJ=B
340 '
350 YY=YS+DY*JJ:Y1=YY
360 KK=A
370 XX=XS+DX*KK
380 FOR T=0 TO TMAX
390 X=XX:Y=YY
400 XX=X-H*SIN(Y+SIN(3*Y))
410 YY=Y+H*SIN(X+SIN(3*X))
420 XXX=L*XX:YYY=L*YY
430 J=12*YYY+240
440 K=12*XXX+240
441 JJ=LL*(J-DA)+240
442 KK=LL*(K-C)+240
450 IF JJ<0 OR JJ>480 THEN 530
460 IF KK<0 OR KK>480 THEN 530
470 GOSUB 670
480 REM 軌跡の線化
490 S=T MOD 2
491 IF S=0 THEN 492 ELSE 494
492 E0=KK:F0=JJ
493 GOTO 495
494 E1=KK:F1=JJ
495 IF S=1 THEN 498 ELSE 496
496 IF T=0 OR T=TMAX THEN 500 ELSE 497
497 LINE (E1,F1)-(E0,F0),CC :GOTO 500
498 LINE (E0,F0)-(E1,F1),CC
500 '
510 PSET (KK,JJ),CC
520 WRITE #1,KK,JJ,CC
530 NEXT T
540 YY=Y1
550 PSET (A,B),2
560 PSET (A+1,B),2
570 PSET (A+2,B),2
580 PSET (A-1,B),2
590 PSET (A-2,B),2
600 PSET (A,B+1),2
610 PSET (A,B+2),2
620 PSET (A,B-1),2
630 PSET (A,B-2),2
631 LOCATE 61,20:PRINT "始点"
632 LOCATE 61,21:PRINT "x(0)=":LOCATE 66,21:PRINT USING "+##.##";X0
633 LOCATE 61,22:PRINT "y(0)=":LOCATE 66,22:PRINT USING "+##.##";Y0
650 GOSUB 3000
651 '
652 CLOSE
653 LOCATE 0,0
660 END
670 REM 軌跡の色
680 IF T>=0 AND T=TT AND T<2*TT THEN CC=1:GOTO 840
700 IF T>=2*TT AND T<3*TT THEN CC=2:GOTO 840
710 IF T>=3*TT AND T<4*TT THEN CC=3:GOTO 840
720 IF T>=4*TT AND T<5*TT THEN CC=4:GOTO 840
730 IF T>=5*TT AND T<6*TT THEN CC=5:GOTO 840
740 IF T>=6*TT AND T<7*TT THEN CC=6:GOTO 840
750 IF T>=7*TT AND T<8*TT THEN CC=8:GOTO 840
760 IF T>=8*TT AND T<9*TT THEN CC=8:GOTO 840
770 IF T>=9*TT AND T<10*TT THEN CC=9:GOTO 840
780 IF T>=10*TT AND T<11*TT THEN CC=10:GOTO 840
790 IF T>=11*TT AND T<12*TT THEN CC=11:GOTO 840
800 IF T>=12*TT AND T<13*TT THEN CC=12:GOTO 840
810 IF T>=13*TT AND T<14*TT THEN CC=13:GOTO 840
820 IF T>=14*TT AND T<15*TT THEN CC=14:GOTO 840
830 IF T>=15*TT AND T<16*TT THEN CC=15:GOTO 840
840 RETURN
850 REM 時刻の表示
860 LOCATE V,8:PRINT 0;"<=t<";T1;"→C=0"
870 LOCATE V,9:PRINT T1;"<=t<";2*T1;"→C=1"
880 LOCATE V,10:PRINT 2*T1;"<=t<";3*T1;"→C=2"
890 LOCATE V,11:PRINT 3*T1;"<=t<";4*T1;"→C=3"
900 LOCATE V,12:PRINT 4*T1;"<=t<";5*T1;"→C=4"
910 LOCATE V,13:PRINT 5*T1;"<=t<";6*T1;"→C=5"
920 LOCATE V,14:PRINT 6*T1;"<=t<";7*T1;"→C=6"
930 LOCATE V,15:PRINT 7*T1;"<=t<";8*T1;"→C=8"
940 LOCATE V,16:PRINT 8*T1;"<=t<";9*T1;"→C=8"
950 LOCATE V,17:PRINT 9*T1;"<=t<";10*T1;"→C=9"
960 LOCATE V,18:PRINT 10*T1;"<=t<";11*T1;"→C=10"
970 LOCATE V,19:PRINT 11*T1;"<=t<";12*T1;"→C=11"
980 LOCATE V,20:PRINT 12*T1;"<=t<";13*T1;"→C=12"
990 LOCATE V,21:PRINT 13*T1;"<=t<";14*T1;"→C=13"
1000 LOCATE V,22:PRINT 14*T1;"<=t<";15*T1;"→C=14"
1010 LOCATE V,23:PRINT 15*T1;"<=t<";TMAX;"→C=15"
1011 RETURN