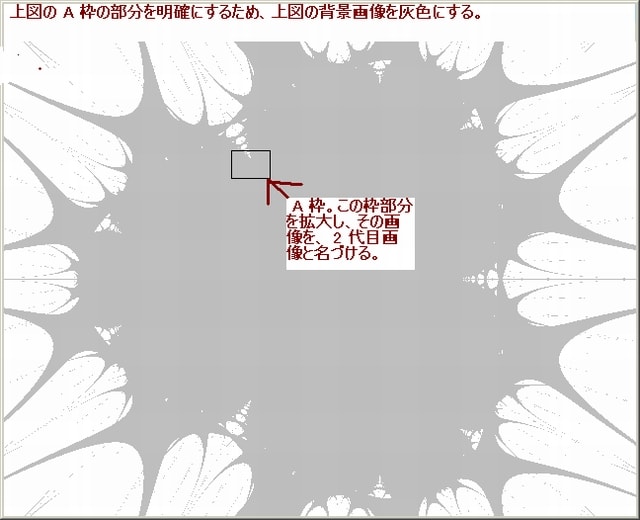
今回の画像は前回の画像:Z^4 +0.456 の中の 5 箇所の部分を拡大してみる。
下図は前回の画像:Z^4 +0.456 である。Nmax=500。

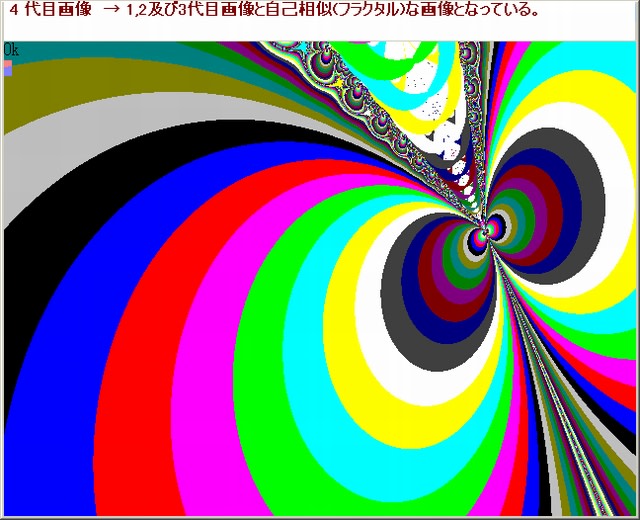
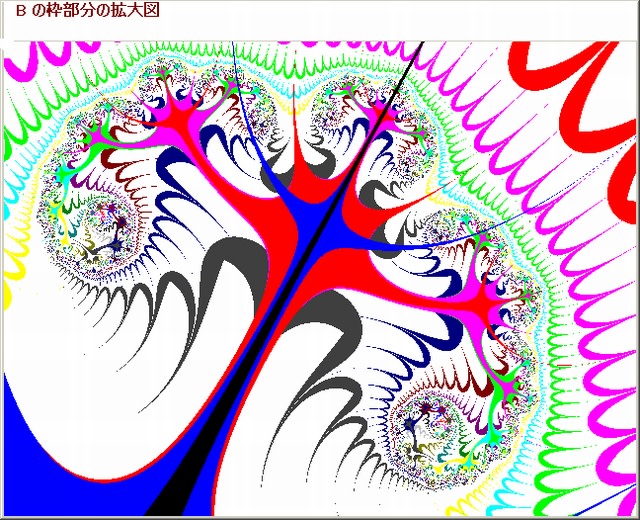
下図は上図の各々1~5 の枠部分の拡大画像である。
1 の部分の画像はNmax=500 の場合とNmax=5000 の場合を求めた。
Nmaxの相違によって画像に差があるかどうか調べ、差はないようだ。
他の画像(2~5)は、Nmax=500である。


---------------------------------------------------


--------------------------------------------------




下図は前回の画像:Z^4 +0.456 である。Nmax=500。

下図は上図の各々1~5 の枠部分の拡大画像である。
1 の部分の画像はNmax=500 の場合とNmax=5000 の場合を求めた。
Nmaxの相違によって画像に差があるかどうか調べ、差はないようだ。
他の画像(2~5)は、Nmax=500である。


---------------------------------------------------


--------------------------------------------------