019 放散虫：Z^3+0.5画像の規則性と不規則性の混在について(その2)

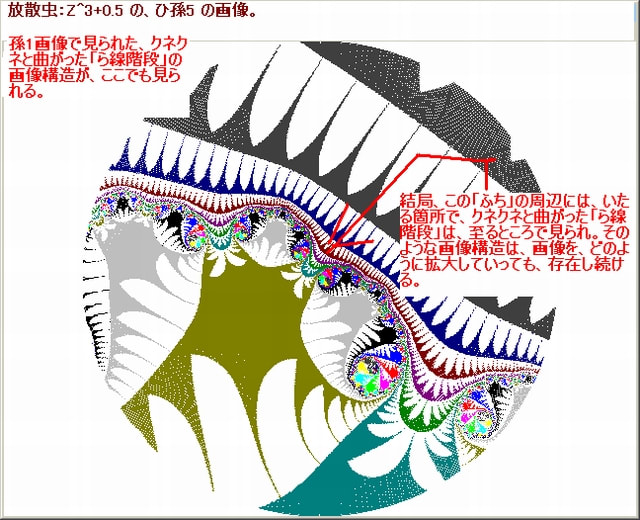
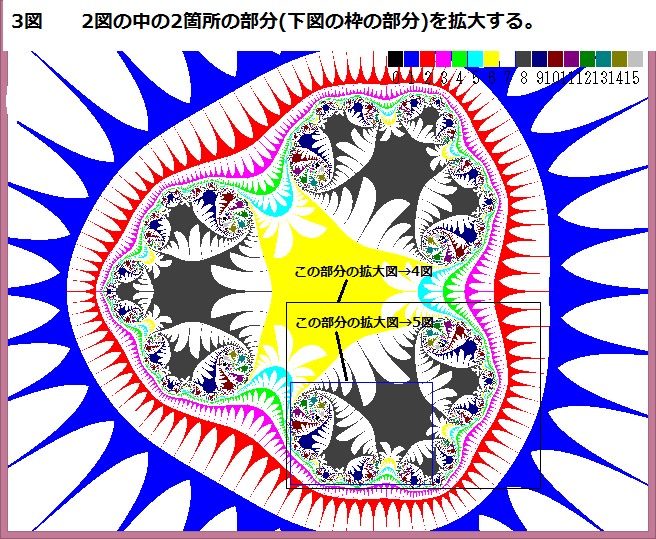
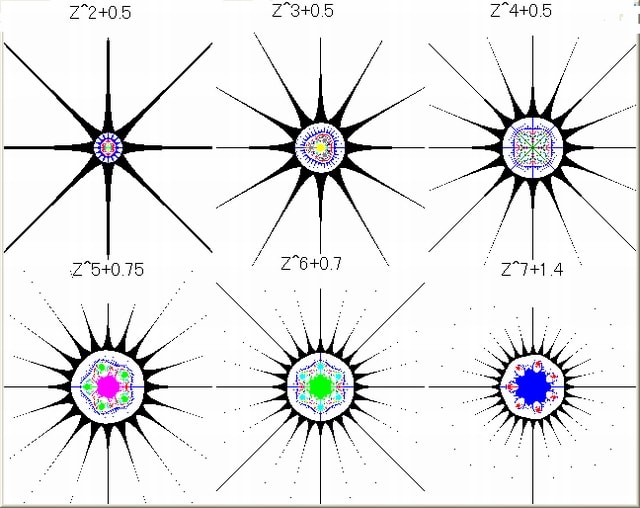
前回の記事018では、N-loop脱出時のX,Yを別々に調べてきたか゛今回は点(X,Y)の挙動を調べてみる。

補足：以下の図1の画像の作成プログラムは記事002の方法2である。複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出時の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。

1.図


調べる箇所は、「内臓」部の一部であるR=0.65のところでRを固定し、θを20度から30度に変化させて、その場合のN-loop脱出時の点(X,Y)の軌跡を調べる。その結果が2.図である。

2.図


上図から分かるように、「内臓」部では、N-loopの入力点(R,θ)に対応した、N-loopの出力点(X,Y)の軌跡が複雑に飛び回るために、その結果として、放散虫：Z^3+0.5の「内臓」部の画像も複雑になっている。
次に、「触手」部であるR=1.3のところでRを固定し、θを0度から60度に変化させた場合の、N-loop脱出時の点(X,Y)の軌跡を3.図に示す。

3.図


上図から分かるように、「触手」部では、N-loopの入力点(R,θ)に対応した、N-loopの出力点(X,Y)の軌跡は単純な変化であるため、その結果として、放散虫：Z^3+0.5の“触手”部の画像も単純になっている。

018 放散虫：Z^3+0.5画像の規則性と不規則性の混在について(その1)

放散虫：Z^3+0.5の画像構造を少し定量的的に調べてみる。
(補足：この画像の作成プログラムは記事002の方法2である。)

記事011で示したように、Z^n+C 画像(但し、n=正整数,C=実定数)は、n 個の全く同一な画像から構成される。従って此の画像を解析する場合、n 個の中の 1 個の部分のみ解析すれば画像全体の構造が分かる。

1.図はZ^3+0.5画像を極座標表示した場合の、θ=0～(2/3)/π までの 1/3 部分である。この部分のみ解析すれば其の結果は全体画像にも言えることになる。
(注：画像の色が今まで記事と異なるのは、N-loop を1→Nmax したためで・・・今迄の画像は 0→Nmaxとしていた・・・あって本質的には今迄画像と同一である。)

1.図



2.図

2.図はRを0→9 変化させたときの、N-loop脱出時のXとYの変化を示した図である。

(補足：1.画像は、複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出後の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。)

2.図の色は、1.図の色と対応させている。この図で分かる大事なポイントの一つは、このXとYの画像が規則的な箇所と不規則的な箇所が混ざっている、ということである。

1.図と見比べてみると分かることだが、規則的な箇所は“放散虫：Z^3+0.5”の「触手」部分であり、不規則的な箇所は「内臓」部分だ。

放散虫：Z^3+0.5の「内臓」部分の画像の複雑さは、XとYの変化の不規則性に依っている。そして放散虫：Z^3+0.5”の「触手」部分の画像の単純さは、XとYの変化の規則性に依っているのだ。R=0～1部分のみを横軸に拡大してみた図が次の3.図である。

3.図

上図は、1.図のRを0→1まで (つまりに「内臓」部での) N-loop脱出時のXとYの変化を示した図である。

(補足：1.画像は、複素平面上の点(R,θ)が画像の表示条件を満足したとき、その点(R,θ)を所定の色で表示している。N-loopの脱出後の(X,Y)を表示しているのでない。ここらへんが混乱しやすいの要注意。)

3図の「内臓」部分でもXとYの規則性と不規則性の混在が見られるが不規則な変化が目立つ。

横軸方向(R方向)のXとYの波形の不連続性は、これらの画像の分解能の不足に拠るものもあると思われるが、画像の感じから言って此れらの画像の不規則な変化は一種のカオス状態になっていることにも拠ると思われる。

この放散虫：Z^3+0.5画像の面白さの要因は、このブログで紹介している他の画像もそうだが此の不規則性と規則性の混在にある、と言えると思われる。

ただ複雑だけの画像や、逆に、ただ単純なだけの画像は退屈で面白くない。
複雑さと単純さの混在こそが画像の面白さの要諦だと思われる。

017 放散虫：Z^3+0.5画像の中のZω点の数？

前記事016で、N-loopを脱出するに要するNをNoとしたとき、No=ωとなるような点Zωの存在を示した(但し、あくまでも「ら線階段」図形からの推定だが)。

点Zωは「ら線階段」の収斂点だから、点Zωの数は画像の中の「ら線階段」の数となる。
記事015において、孫1画像の中の4部分を選び其れらの画像を拡大してみた。

其れらの画像の各々には無数の「ら線階段」があった。
(要するに孫1自身のフラクタル画像が無数に存在していた。)

従って無数のZω点が存在していることになる。

其れらの画像・・・即ち孫1の部分画像・・・を見る限りにおいて、無数は無限と言い換えてもよいと思われる(ここに思考の一つの飛躍があるが)。

その無限の大きさ(濃度)を仮にℵaとしよう。

***

さて孫1画像にはZω点はℵa個あることになるが、Z^3+0.5画像は其のフラクタルな画像も無限個ある。なぜなら或る部分(例えば記事014の子1画像のAの部分)の拡大は無限に可能だからである。その無限の大きさ(濃度)を仮にℵbとしよう。

***

さてZ^3+0.5画像の中のZω点の濃度は ℵa*ℵb としてよいだろうか？

ここらへんのことは私は自身はないが、ともかく Z^3+0.5画像のZω点の濃度については私の興味がある。其れは此のZ^3+0.5画像の魅力の一つである。

016 放散虫：Z^3+0.5画像の「ら線」構造ついて

1.図


2.図


1.図は、放散虫：Z^3+0.5 の孫1 画像を反時計方向に70度回転させた画像である。

2.図は色の説明図である(記事002で説明している。参考のため再掲した。)

1.図から分かるように此の放散虫：Z^3+0.5 の 孫1 画像は「ら線階段」を連想させる画像構造となっている。

そして其の「階段」は或る1点へと収斂している。
この図に書いた数値は其の各「階段」での色を示す数値(カラーコート値)である(2.図を参照)。

1.図から分かることは、此の「ら線階段」は、N-loop脱出時のN値を1ずつ増加させながら、複素平面の或る1点へと収斂している、ということだ。

その収斂点へ向かう程、N-loopを脱出するに必要なN値(No)は増加していく。

そして此の収斂点へ向かう過程は永遠に続くと思われる。
つまり、Noが、いかに大きくなっても其の収斂点には決して到達しないだろうと思われる。

この過程は無限に続くのだが、No値は、一つずつ増加していくわけだから、此の無限の大きさは、いわゆる可算無限だと思われる。

0を含む自然数数全ての集合をωと名づけたとき、この収斂点ではNo=ω表現できると思われる。

そして此の複素平面上の収斂点を便宜上Zω=Xω+iYωと名づけることにすると、「ら線階段」は点Zωへ収斂していく、とも言えそうだ。

さて、問題は此のようなZωは此の放散虫：Z^3+0.5 の 孫1 画像の中に「いくつ」在るのだろうか？　ということだ。

この問題については以下の記事で考察する。

015 放散虫：Z^3+0.5画像のフラクタル性(その4)

下図は、前画像014で示した孫1画像である。この画像の中の5箇所の部分(A～D)を拡大する。それらの画像を便宜上、それぞれ「ひ孫画像1」～「ひ孫画像5」と名付ける。なお各画像の説明は各画像に書いてある。








------------------------------------------------------
記事012より今迄見てきた画像から下記のことが言える。

放散虫：Z^3+0.5 画像の”内臓”部の画像は、3個の同一な画像から構成されている。
そして其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されている。
そして更に其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されていて・・・・。このような画像構造が永遠に続いている。

そして又その3個の画像には、それぞれ、1点へと収束していくクネクネと曲がった「ら線階段」が無限に存在する、ということである。

即ち、3個の画像を、どのように拡大していっても、3個の自己相似な画像が永遠に存在する。そして其の画像は、1点へと収束していくクネクネと曲がった自己相似な「ら線階段」が無限に存在する、ということである。

この無限の自己相似性の二重構造が、放散虫：Z^3+0.5　の「内臓」部の画像構造になっている。これは何とも複雑な構造だ。

こんな複雑な構造自体を知らなくても、放散虫：Z^3+0.5　の「内臓」部の画像を見て何となく奇妙で面白い感じをもつのは、我々が此の画像の或る秩序をもった複雑性を直感的に感じ取っているからだろう。

014 放散虫：Z^3+0.5画像のフラクタル性(その3)

前記事013の子1画像の中の一部を拡大し、それを孫図と名付ける。


下図は孫図であるが画像構成は子1画像と全く同じ(フラクタル)である。
(この孫図の中の4箇所の部分(A～D)を更に拡大する。)



拡大図(A～D即ち孫1～孫4)は以下のようになる。
(各画像の特徴は各画像に書いてある。)

013 放散虫：Z^3+0.5画像のフラクタル性(その2)

放散虫：Z^3+0.5画像を極座標表示させる。この画像を便宜上、親画像と名付ける。


上の親画像の中の4箇所の部分(A～D)を拡大する。
それぞれの画像を便宜上、A→子1,B→子2,C→子3,D→子4と名付ける。
(注：以後の記事で画像を順次拡大していくため上記のように名づける。)

以下の図から分かるように子1～子4は全く同じ画像構造となっている。

012. 放散虫:Z^3+0.5画像のフラクタル性(その1)

放散虫:Z^3+0.5を拡大していくと1図のようになる。


放散虫：Z^3+0.5の内臓部は2図のようになる。



3図に示すように2図の中の2箇所の部分を拡大する。



-----------------------------------
前記事011で示したように、Z^3+0.5画像は3個の同一画像から構成されている。
それらの3個の同一画像は、更に3個の部分から構成されていることが、3図、4図より分かる。また其れらの画像は入れ子構造となっていることが分かる。
この入れ子構造は無限に続いている。

011. 「放散虫」：Z^n+C 画像について。但しn=正整数、C=実定数 の場合。

Z^n+C 画像(但しn=正整数、C=実定数)画像例を以下に示す。

1図

2図

3図

2図は1図の拡大図(「内臓部」)である。
----------------------------------------------
これらの図の画像作成条件の概略は以下のとおり。
1.N-loop脱出条件：X^2+Y^2>100
2.pset条件：|X|<10 or |Y|<10
3.色:C=No mod 16 (NoはN-loop脱出時のN値)
----------------------------------------------
上図から分かるように『Z^n+C (n：正整数 ,C：実数)の画像は『同形なn個の画像から構成されている。』
この『・・・』の命題が正しければ、このような画像の分析は、n個のうちの1つの画像を調べれば其の調査結果は其の画像全体についての結果になる。　この記事の後で、ちょっとした画像分析をしたいと思っているので、『・・・』が正しいかどうかを調べる。
この程度の問題なら私でも解けそうだ。そこで、昔々の学生時代を偲びつつ証明しよう。
-----------------------------------------
[命題]
『nが正整数、Cが実定数のとき、複素関数：Z^n+Cの“放散虫”の画像は、原点を中心とした扇状にn分割された各領域で、同一な画像から成立している。』

[証明]
複素平面を原点(0,0)を中心として扇状に、同じ大きさにn分割する。第1番目の分割領域内の点(X,Y)を極座標表(R,θ)表示すると、Z=X+iY=R*e^iθとなる。ここで、R=(X^2+Y^2)^0.5,　θ=arctan(Y/X)である。

次に、任意の正整数をm ( < n ) とし、第m番目の分割領域について考える。 Rを一定値にしてθを(2π/n)*m (radian) 回転させると、点(X,Y)は、第m番目の分割領域に移動する。その点を(Xm,Ym)とすると、その点は、Z=Xm+iYm=R*e^i(θ+(2*π/n)*m)となる。

ここで、Z^nを、分割領域1及び分割領域mについて求めてみる。

分割領域1では、Z=R^n*e^i(n*θ)となる。
次に分割領域mでは、Z=(R*e^i(θ+(2*π/n)*m))^n=(R^n)*(e^i((θ+2*π/n)*m*n)=(R^n)*(e^i(n*θ))*e^(i*m*2*π) = (R^n)*e^i(n*θ)(cos(2*m*π)+i*sin(2*m*π)=(R^n)*e^i(n*θ)となり、領域1でのZ^nと一致する。　
(注：cos(2*m*π)=1, sin(2*m*π)=0)

従って、Rを固定値としたとき、領域1と領域mでのZ^n値は全く一致するため、それらの領域での、点(X,Y)と点(Xm,Ym)の挙動は全て一致する。故に、これらの挙動の結果生ずる、任意の条件化下の図形表示は、n分割された領域のそれぞれで、全て一致することになる。

(補足：画像全体の作成手順の概要は、始めRを初期値に固定しθ=0→2πと変化させて計算し、次にRを次の値に固定し、θ=0→2πと変化させて計算する。これを繰り返す)
以上より、複素関数：Z^n+C　の図形は、原点を中心としてn分割された領域で、全く同一の画像から構成されることになる。
(証明終り)

なお、この証明の正しさを確認するため、Z^3の場合について、N-loopの入出力での点(X,Y)の軌跡を調べた。その件については、このブログの後の記事で掲載する予定。