364 複素関数：(1+iA)cosZ で実変数Aを変えた時のジュリィア集合の変化

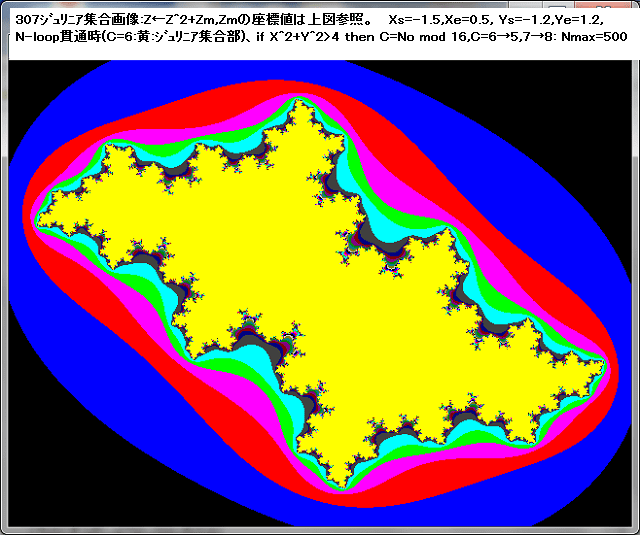
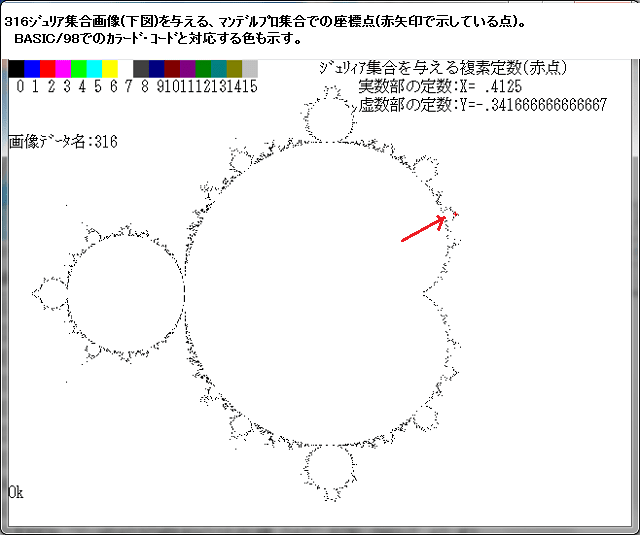
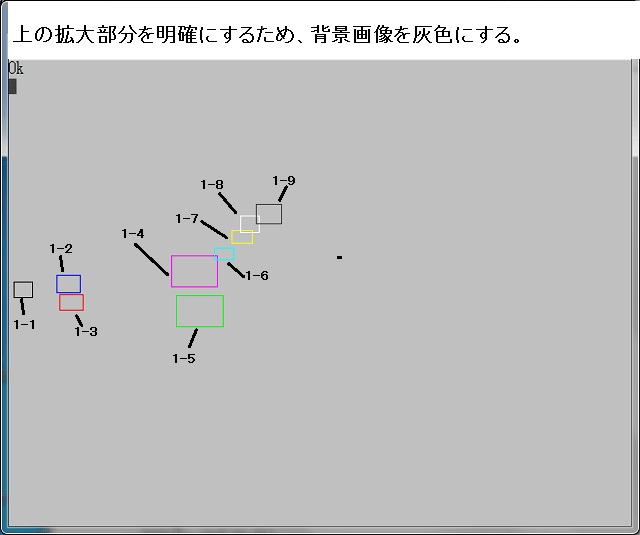
複素関数：(1+iA)cosZ において、Aを実数として変化させた時の、ジュリィア集合の変化を調べる。
但し、ここで、Nmax=50として、N-loop脱出(発散)条件を、X^2+Y^2>1000としたときとし、その場合の色を、C=No mod 16,C=7→8,2→3とする。N-loop貫通時にはC=2(赤)とし、その赤部分をジュリィア集合とする。(注：この条件を変えればジュリィア集合の形態は変わってくるが、ここでは上記の場合をジュリィア集合と定義する。)
***
この場合の、Aを変化させた時の図を下に示す。Aが大きくなるにつれて、ジュリィア集合は分散していく様子が分かる。

***
(1+iA)cosZの実数部と虚数部を求める計算は参考として最後に書いておく。
***





***

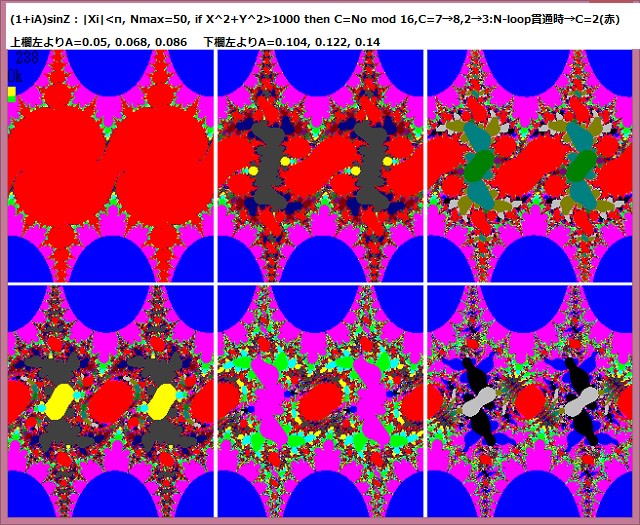
下図はAの範囲を大きくした場合。





---------------------------------------
(参考)　

(1+iA)cosZの実数部と虚数部を求める計算は下記のとおり。
f(Z)=(1+iA)sinZ=(1+iA)(sinXcoshY+icosXsinhY)
従って、
Re.f(Z)=sinXcoshY-AcosXsinhY
Im.f(Z)=cosXsinhY+AsinXcoshY

363 サンマルコ・ジュリニア集合画像と其の部分拡大図

サンマルコ画像と言われている画像がある。これはジュリィア集合画像であるが、その形がサンマルコ聖堂に似ているから、そう言われるのだろう。以下の画像が私流の其の画像である。画像条件は以下のとおり。
***
複素関数：coshZ-2.25
発散条件と色：if X^2+Y^2>2500 then 色C=No mod 16,C=7→8,2→3,Nmax=40
収束時(即ちN-loop貫通時。此れがジュリニア集合部分となる)→C=2(赤)とする。
画像表示座標：XS=-4.2,Xe=4.2,Ys=-3.15,Ye=3.15

***

下図から分かるように、ミニ・サンマルコ・ジュリニア集合(赤色)が随所に存在する。



***





-----------------------------------------

362 マンデルブロ集合周辺部のジュリニア集合画像 (その3)

Z^2マンデルブロ集合周辺部のジュリニア集合の全体画像及びジュリニア集合そのものの画像を示す。
下図のマンデルブロ画像の周辺画像は厳密には周辺ではなく、その概略を示すもので、Z^2マンデルブロ集合の真の周辺より外部にある。

***
複素平面の点をZmとするとき、点列：Z←Z+Zmが発散しない場合、即ち、N-loopを貫通する場合には、その点Zmに対応したジュリニア集合が存在し、点Zmが異なれば、その場合のジュリニア集合の形態も異なってくる。
------------------------------------------



-------------------------------------------





-------------------------------------------





--------------------------------------------





-------------------------------------------





------------------------------------------



------------------------------------------



------------------------------------------



------------------------------------------



------------------------------------------





-----------------------------------------





-----------------------------------------



----------------------------------------





-----------------------------------------



---------------------------------------------

361 記事357において、ジュリィア集合のみの表示

前記事360同様に 記事357において、ジュリィア集合のみの表示する。

なお、下図のマンデルブロ画像の周辺画像は厳密には周辺ではなく、その概略を示すもので、Z^2マンデルブロ集合の真の周辺より外部にある。
-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



----------------------------------------------



----------------------------------------------



-----------------------------------------------



----------------------------------------------



---------------------------------------------



---------------------------------------------



---------------------------------------------



---------------------------------------------



--------------------------------------------

360 記事356において、ジュリィア集合のみの表示

今までのジュリィア集合画像(記事352,355～129)においては、ジョリィア集合そのものだけでなく、ジュリィア集合へ至る過程の部分も表示してきた。

即ち、Z←Z^2+λ点列において、N-loop脱出時のN値をNoとしたとき、N-loopを脱出する場合も、色C=No mod 16として表し、N-loopを貫通する場合(即ち、点列が収束する場合→此れがジュリニア集合となる場合)は、C=6(黄色)で表してきた。
***
以下の画像は、記事356の場合のジュリニア集合のみを表示する(但し、その一部のみ)。下図は、マンデルブロ集合の赤点での座標のジュリニア集合を示している。

下図から分かるように　(今までも繰り返し書いてきたが)　ジュリニア集合の形態は、Z←Z^2+λ点列のλに強く依存する。λがマンデルブロ集合内にあれば、ジュリニア集合は一つ塊となり、λがマンデルブロ集合の周辺では、ジュリニア集合の形態は複雑となり、その形態は、λにより変幻自在に変化する。λが少しでも異なればジュリニア集合の形態は全く異なってしまう。

λはマウスで指定しているが、マウスの指定位置が少しでも違えばジュリニア集合の形態は全く異なってしまう。ジュリニア集合の面白い形態を探すのは試行錯誤でしか発見できないが、Z^2マンデルブロ集合の周辺部の『こぶ』付近は、ジュリニア集合の面白い形態が多そうだ。

なお、下図のマンデルブロ画像の周辺画像は厳密には周辺ではなく、その概略を示すもので、Z^2マンデルブロ集合の真の周辺より外部にある。

----------------------------------------------------




---------------------------------------------------




---------------------------------------------------





---------------------------------------------------





---------------------------------------------------





---------------------------------------------------





---------------------------------------------------





---------------------------------------------------





--------------------------------------------------





--------------------------------------------------





-------------------------------------------------





-------------------------------------------------





-------------------------------------------------





-------------------------------------------------





------------------------------------------------





-----------------------------------------------

359 前記事358の319図の画像構造について

前記事358の画像は、N-loop脱出時のNをNoとしたとき、色C=No mod 16 (但し、C=6→5,7→8)としている。

319図の画像構造は、図の中央部の2箇所及び上下の2箇所より、竜巻状の色の変化、即ちNoの変化が生じていることがわかる。色Cは16色しかないので、Cの変化(Noの変化)は16進法で変化している。
***
その変化の様子は、竜巻状のモノが随所で分岐していて、その分岐の本体は渦巻状となって、特定の座標点へと収束していく。その収束点は、319図の拡大図 (図319-1～図319-5) から分かるように、随所に存在している。
***
このような画像構造は、このブログの画像に、よく見られる画像構造であって、自己回帰の点列：Z←f(Z) の画像の特徴と思われる。Cの変化は其の色の変化から分かるように、Noは連続して　(即ち、1ずつ増加or減少して)　変化していく。色Cを実数的に連続が可能だとすれば、即ち、Noを実数的に連続させれば、画像構造の変化は、実数的に連続していると思われる。
***
Noの変化　(即ち、色Cの変化)　の様子を分かり易く見るために、Noが偶数の時は赤、奇数の時は黒で表示して見る。ここで、記事352,355～記事358の画像は全てNmax=500であるが以下の赤黒縞模様の画像はNaを500以下の数として、赤黒縞模様画像は、No＜Naの場合のみ表示させている。そうすることによって画像構造が分かり易くなるためである。
以下、記事358の各画像と其れの赤黒縞模様画像を並べて表示する。
-------------------------------------
・319 画像





-----------------------------------
・319-1 画像





------------------------------------
・319-2 画像





-----------------------------------
・319-3 画像





----------------------------------
・319-4 画像





-----------------------------------
・319-5 画像

358 記事356の319図の中の部分の拡大図

記事356で、Z^2マンデルブロ集合周辺の赤印を付けた座標でのジュリィア集合の画像を求めた。

これらの画像の319画像のジュリニア集合画像の中の5箇所の部分を拡大してみる。

なお、ジュリィア集合(即ちN-loopを貫通する場合、換言するとZn点列が収束する場合)は、ジュリィア集合部分は、記事356の各画像で黄色で示しているが、319画像は黄色の部分は存在しない。従って、この画像では本来の意味でのジュリィア集合は存在しない。

しかし、マンデルブロ集合の周辺での座標が少しでも変われば、黄色部分は現れたりして、本来の意味でのジュリィア集合(黄色の部分)の有無は、Z^2マンデルブロ集合周辺の座標に敏感に依存している。

------------------------------------





------------------------------------





------------------------------------

357 マンデルブロ集合周辺部のジュリィア集合画像(その2)

前記事356の続きの画像である。
説明は前記事356を参照のこと。
--------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



-------------------------------------



------------------------------------



------------------------------------



------------------------------------



--------------------------------------

356 Z^2マンデルブロ集合周辺部のジュリィア集合画像(その1)

Z^2マンデルブロ集合の周辺部分の点Zm(=Xm+iYm)としたとき、Z←f(Z)+Zm のジュリィア集合画像を求める。
今回以降の記事ではf(Z)=Z^2とする。

点Zmは、下図のZ^2マンデルブロ集合の周辺画像の任意の点をマウス・クリックで与えている。
但し、下図のZ^2マンデル集合周辺画像は正確なZ^2マンデルブロ集合部ではなく、その接近した外側部である。
Zm点は赤の十字マークで示している。その点が分かるように赤い線で、その位置を示している。

***
そのZm点でのジュリィア集合画像を、Z^2マンデルブロ集合周辺画像の下図に示した。

このジュリア集合画像は、Zm点を1dotでも、ずらすと変化してしまう。
ジュリニア集合画像自体が、Zm点に強く依存している。
***
下図のジュリィア集合部分は黄色(C=6)の部分であり、Z←f(Z)+Zm点列が収束する部分である。

このジュリィア集合部分の画像構造が、Zm点に強く依存しており、Z^2マンデルブロ集合の周辺で著しく変化する。

マンデルブロ集合内では、ジュリィア集合画像構造は単純な「塊(かたまり」となり、マンデルブロ集合の外側ではジュリィア集合部分は無くなる。

***
ジュリィア集合画像構造が面白いZm点は、マンデルブロ集合の近接した周辺座標であるが、その画像構造はZmで変幻自在に変化していることが分かる。

------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



-------------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------



-----------------------------------



-----------------------------------



------------------------------------



------------------------------------



------------------------------------



------------------------------------

355 Z^2-1のジュリア集合(その2)

記事352の画像:1-1画像の中の5個所の部分を拡大する。

マンデルブロ画像と違って、Z^2-1のジュリア集合画像は、ジュリア集合周辺部の画像も、ジュリア集合に接近するにつれて、単純に、Noが連続的に1ずつ増加していき、マンデルブロ集合のような複雑なNoの分布はしていないことが分かる。画像としては単純で面白くはない。

--------------------------------------------------









-----------------------------------------------

352 Z^2-1のジュリア集合(その1)

複素関数f(Z)において、nを0を含む自然数とするとき、循環点列
Z(n+1)←f(Zn),n=0,1,2,4,・・・を考える。

複素平面において、始点をZ0から始め、|Zn|>2となったき、複素平面に点Znをpsetする。

N-maxにおいても|Zn|>2とならない(即ち、N-loop貫通時。収束時。)の点Znの集合をジュリア集合と、ここでは名付ける。以下の画像は、f(Z)=Z^2-1の場合の画像である。
***

各画像の左上に表示した色コードより、Noの値はジュリア集合部(黄色)に近づくにつれて、1ずつ増加していることが分かる。BASIC/98は16色しか使用できないので、16進で増加していることになる。

--------------------------------------------

下図の黄色の部分がジュリィア集合である。この画像のBASIC/98のプログラムを最後に書いておく。



---------------------------------------------




--------------------------------------------



















------------------------------------------------------------
一番上の画像(Z^2-1のジュリニア集合画像のBASIC/98のプログラム。

5 REM Z^2-1 ジュリニア集合
10 REM Xの範囲を与え、XDOT:YDOT=640:480,DY=DX=(XMAX-XMIN)/XDOT
20 REM OPEN,WRITE 含む
30 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",31,ALL
31 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",32,ALL
32 ON ERROR GOTO 50000
40 CONSOLE ,,0,1
50 COLOR 0,7,,,2
60 CLS 3
70 GOSUB 10000
80 OPEN "C:\BASIC\RUN\DATA.DAT" FOR OUTPUT AS #1
81 OPEN "C:\BASIC\RUN\親DATA.DAT" FOR OUTPUT AS #2
90 REM Xの範囲を与えてYは自動設定
110 XMIN=-1.6 :XMAX=1.6
120 REM X,Yのdot数
130 XDOT=640:YDOT=INT(XDOT*480/640)
140 REM X,Yの実行ステップ幅
150 DX=(XMAX-XMIN)/XDOT :DY=DX
151 YMIN=-DY*YDOT/2:YMAX=-YMIN
152 WRITE #2,XMIN,XMAX,YMIN,YMAX,DX,DY
160 FOR J=0 TO YDOT
170 FOR K=0 TO XDOT
180 X=XMIN+DX*K
190 Y=YMIN+DY*J
200 FOR N=0 TO 50
210 X1=X
220 X=FNR2(X,Y)-1
230 Y=FNI2(X1,Y)
240 REM 発散条件
250 Q=X^2+Y^2
260 IF Q>4 THEN 290 ELSE 270
270 NEXT N
280 C=6 :GOTO 330
290 REM 発散した時点での点(X,Y)のpset条件
310 C=N MOD 16
320 IF C=7 THEN C=8
321 IF C=6 THEN C=5
330 PSET(K,J),C
340 WRITE #1,K,J,C,N
350 NEXT K
360 NEXT J
370 CLOSE
380 END