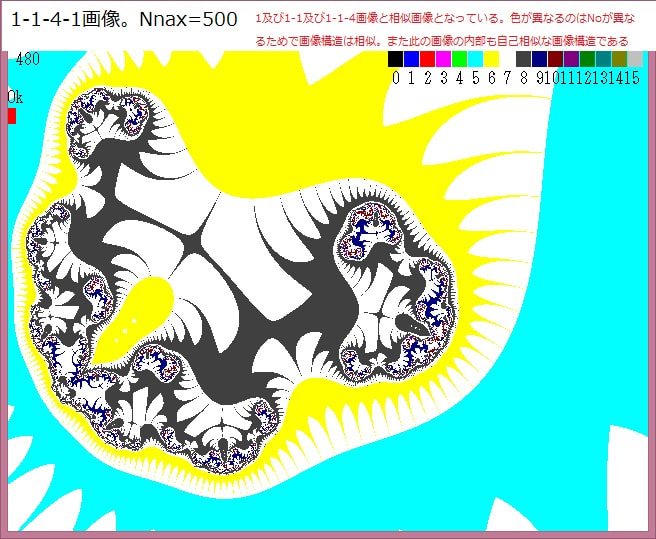
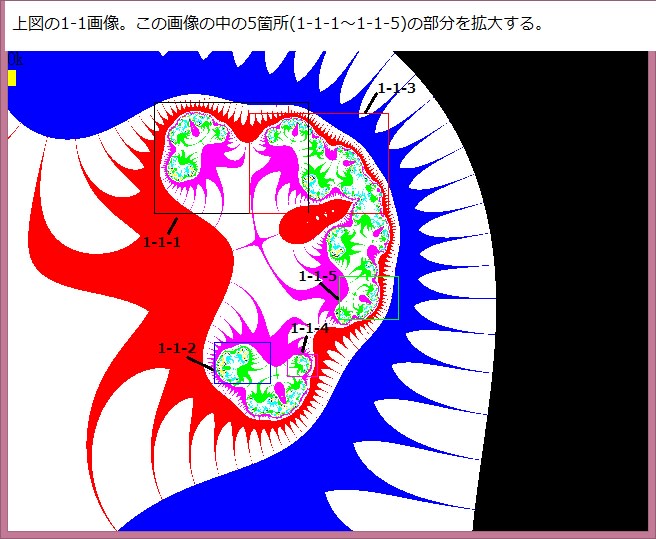
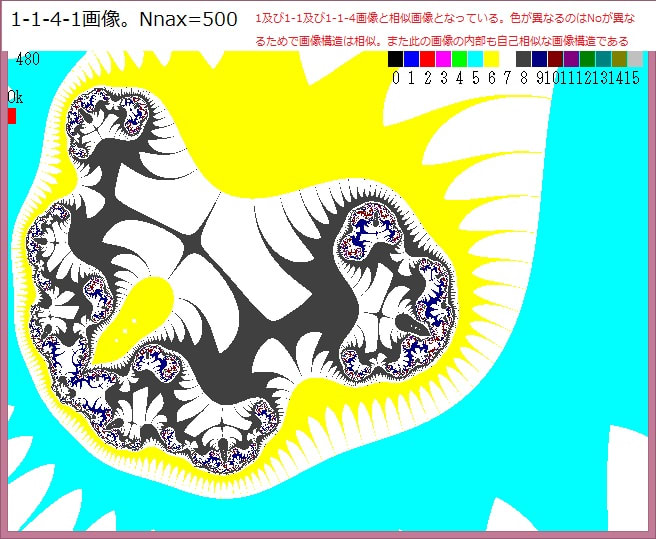
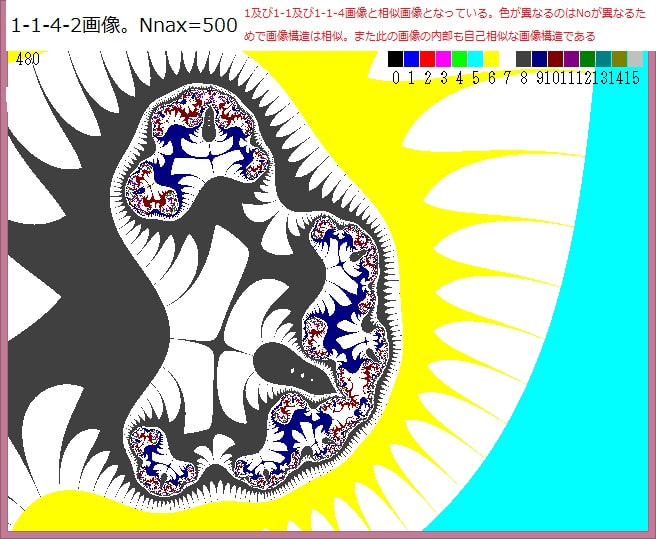
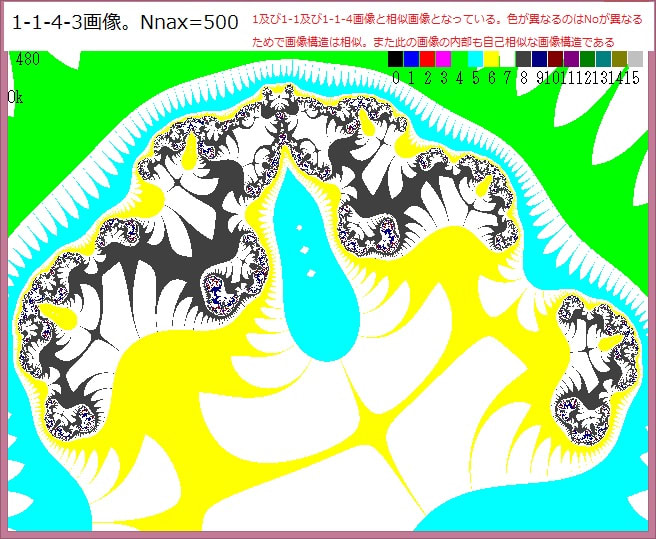
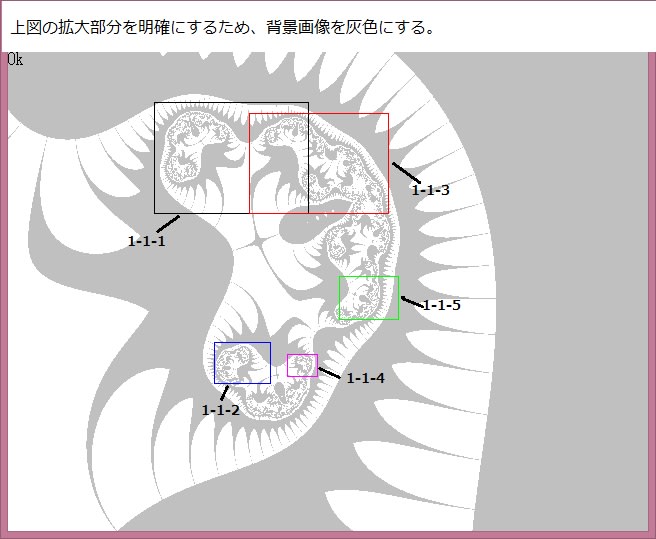
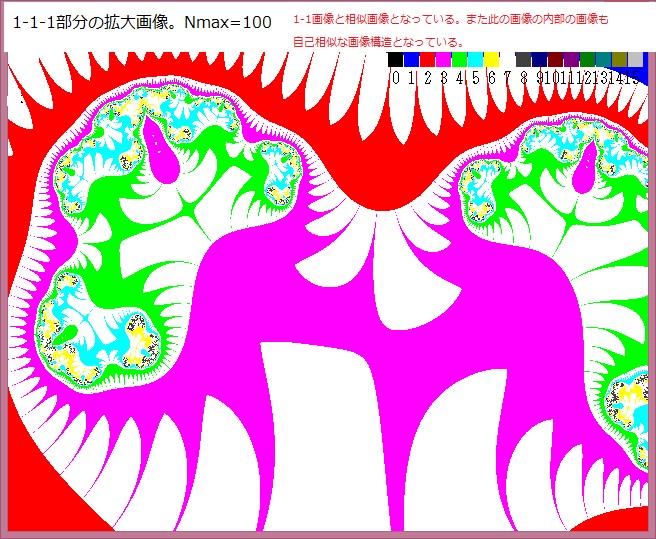
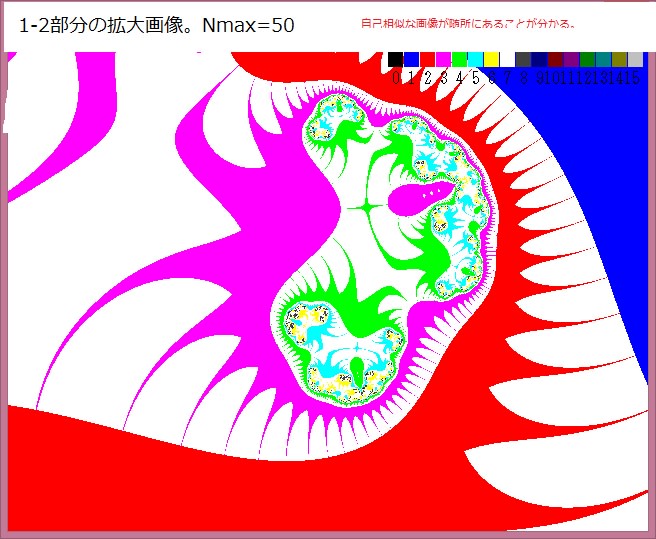
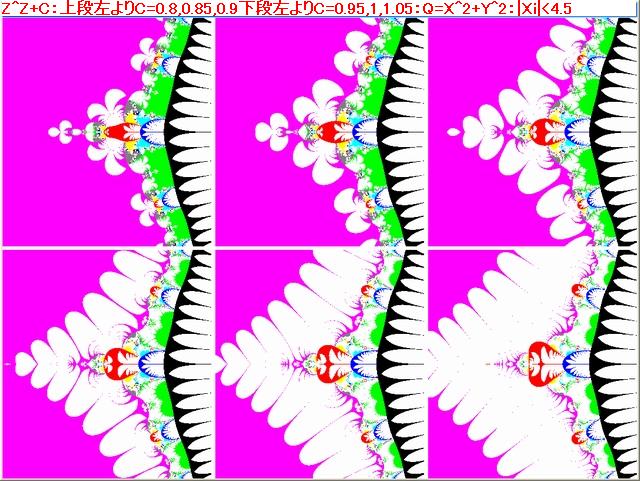
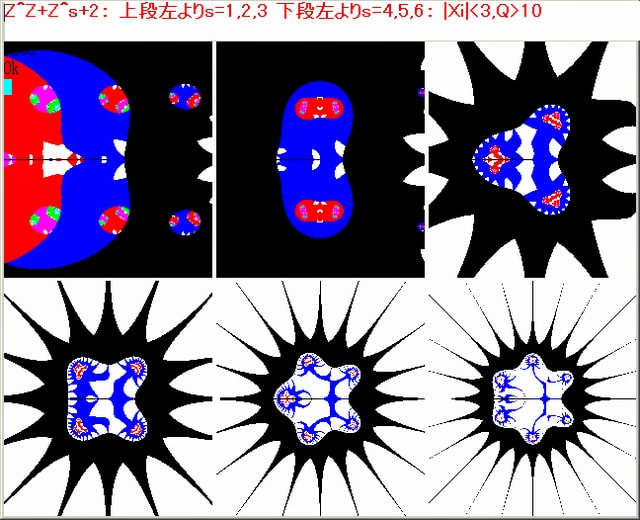
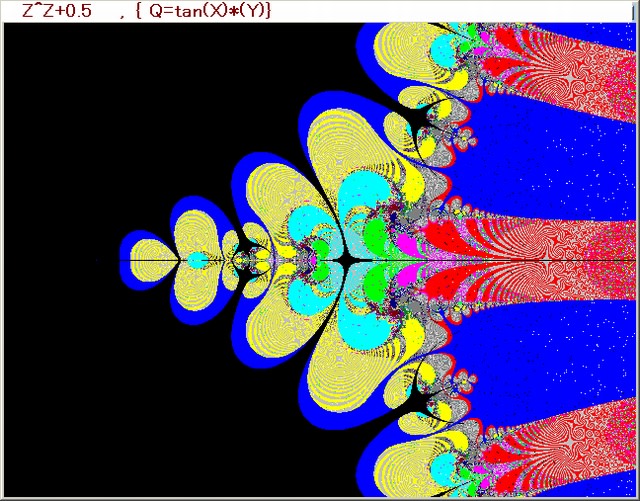
下図は以下の画像である。
・複素関数:Z^Z+Z+0.5
・Nmax=50
・R=0→1 注:この条件が前記事より異なる。
・θ=-π→+π (注:θ=+π→-πでも画像は同じになる)
・N-loop脱出条件及びpset条件を各図で変えている。
その条件は各図に書いてある。
以下、画像の掲載順に其の条件を書いておく。
1.Q=X^2+Y^2 , if (Q>100 & (|X|<10 or |Y|<10)) then pset
2.Q=1/(|X|*|Y|), if (Q>100 & (|X|<10 or |Y|<10)) then pset
3.Q=1/log(|X|*|Y|), if (Q>100 & (|X|<10 or |Y|<10)) then pset
4.Q=1/(sinX*sinY), if (Q>100 & (|X|<10 or |Y|<10)) then pset
-------------------------------------------------------------
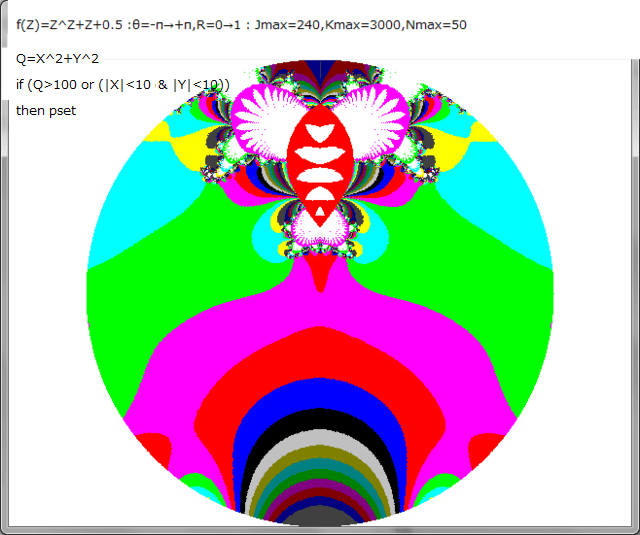


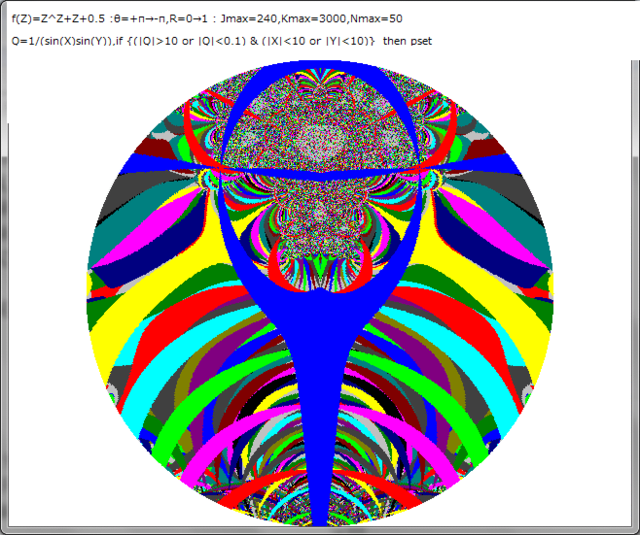
・複素関数:Z^Z+Z+0.5
・Nmax=50
・R=0→1 注:この条件が前記事より異なる。
・θ=-π→+π (注:θ=+π→-πでも画像は同じになる)
・N-loop脱出条件及びpset条件を各図で変えている。
その条件は各図に書いてある。
以下、画像の掲載順に其の条件を書いておく。
1.Q=X^2+Y^2 , if (Q>100 & (|X|<10 or |Y|<10)) then pset
2.Q=1/(|X|*|Y|), if (Q>100 & (|X|<10 or |Y|<10)) then pset
3.Q=1/log(|X|*|Y|), if (Q>100 & (|X|<10 or |Y|<10)) then pset
4.Q=1/(sinX*sinY), if (Q>100 & (|X|<10 or |Y|<10)) then pset
-------------------------------------------------------------