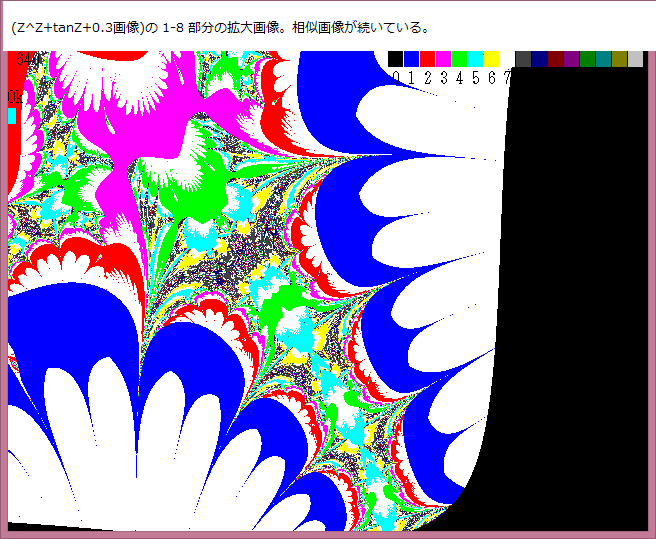
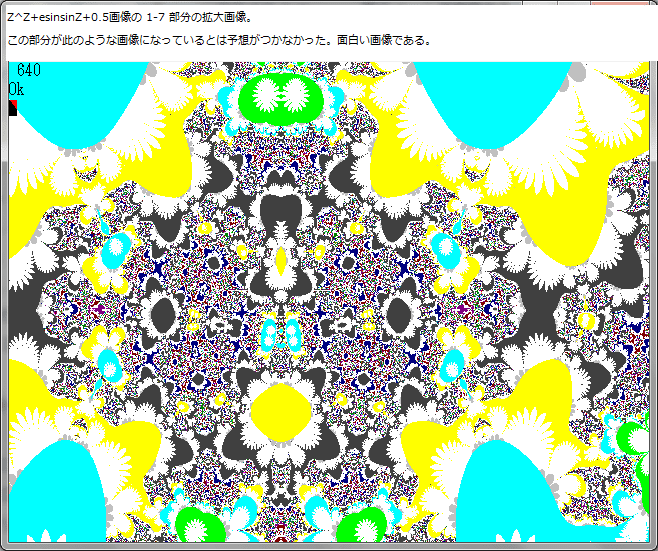
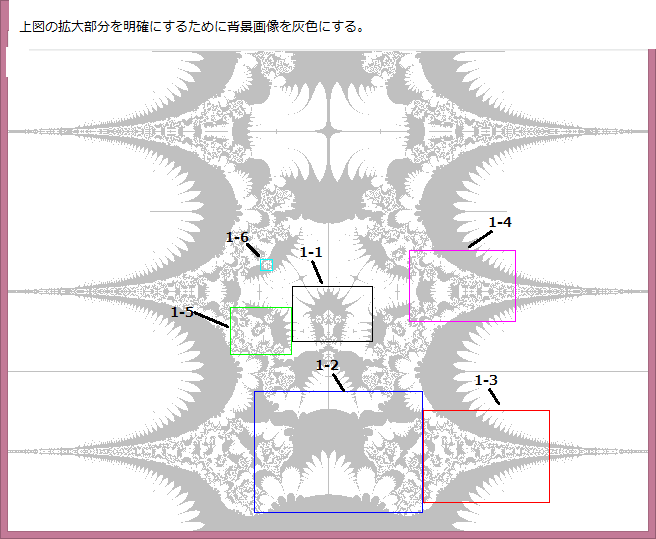
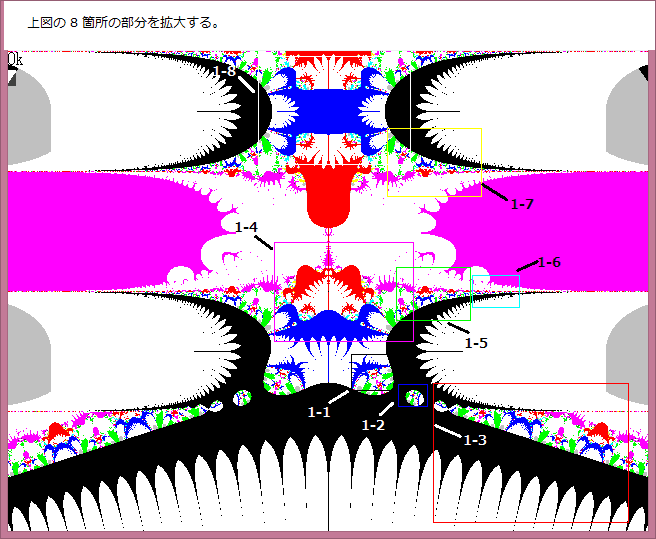
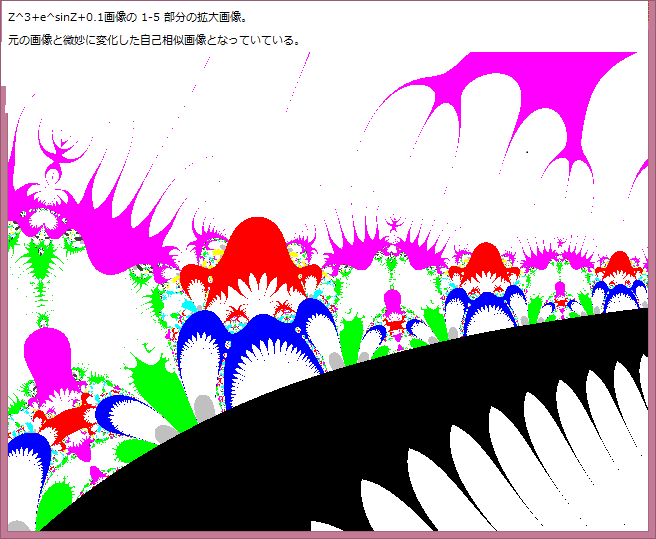
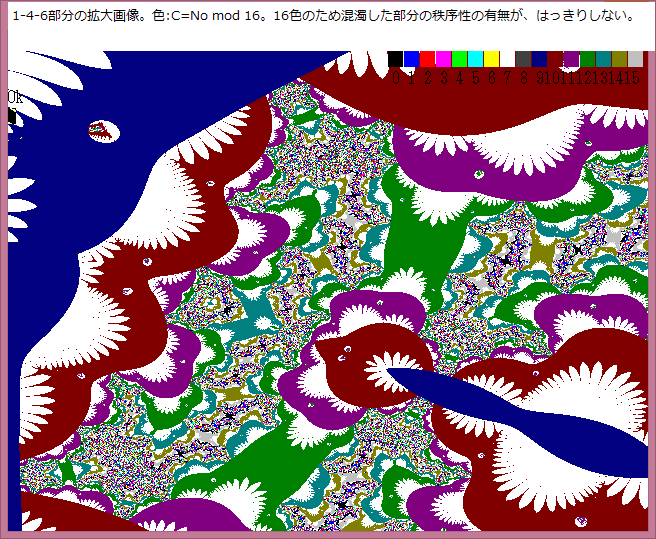
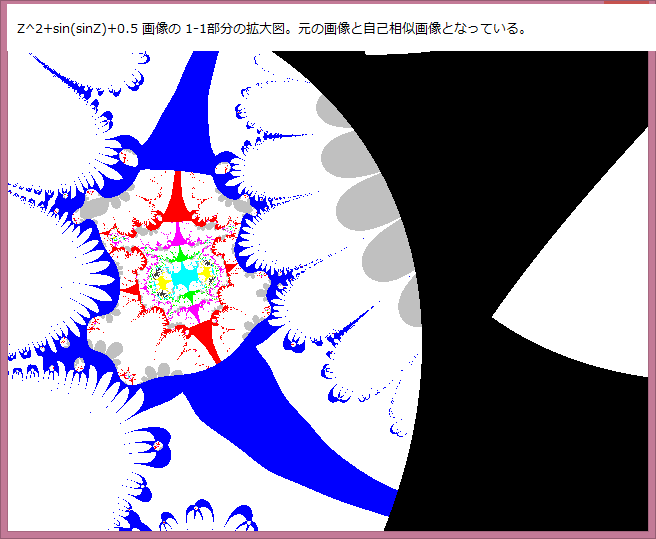
前記事523において、Noが不規則に変化する部分は Z^Z+tanZ+0.3画像の中の 1-2部分である。


上図の1-2部分の拡大図が下図である。

この1-2画像の横軸の中央から縦軸を切った線での No を調べてみたグラフが下図である。

上図を見ると一見して No に規則性があるとは思えない。
厳密には此のグラフをフーリエ変換して調べれば、このグラフを特徴づけている周波数が分かるだろう。しかし私はフーリエ変換の方法を忘れてしまったし、現在そこまで挑戦する気力は残念ながらない。
ただ、No には歴然とした規則性はないと分かっただけで満足しよう。
***
この 1-2画像を見て分かるのは中央線を堺に左右対称であることである。
そして此の図から或る連想を生じさせることである。
私は『何か生物のミイラの顔』を連想した。また人によっては『耳の広がったネズミの顔』を連想するかも知れない。この画像の横軸の下側の左右に『目』のようなモノが在るからである。
こういう連想を生じさせる背景には、画像全体における No の何らかの規則性が存在している故かも知れない。もし其のような規則性が存在したとしても其れを定量的に示すには大変困難だろう。此の画像は、三角形とか円とかの単純な形の単純な構成の画像構造ではないからである。
しかし、このブログの絵作りの目的は其のような数学的分析ではなく、
画像として面白いか否かにあって、此の1-2画像は私には確かに面白いのである。


上図の1-2部分の拡大図が下図である。

この1-2画像の横軸の中央から縦軸を切った線での No を調べてみたグラフが下図である。

上図を見ると一見して No に規則性があるとは思えない。
厳密には此のグラフをフーリエ変換して調べれば、このグラフを特徴づけている周波数が分かるだろう。しかし私はフーリエ変換の方法を忘れてしまったし、現在そこまで挑戦する気力は残念ながらない。
ただ、No には歴然とした規則性はないと分かっただけで満足しよう。
***
この 1-2画像を見て分かるのは中央線を堺に左右対称であることである。
そして此の図から或る連想を生じさせることである。
私は『何か生物のミイラの顔』を連想した。また人によっては『耳の広がったネズミの顔』を連想するかも知れない。この画像の横軸の下側の左右に『目』のようなモノが在るからである。
こういう連想を生じさせる背景には、画像全体における No の何らかの規則性が存在している故かも知れない。もし其のような規則性が存在したとしても其れを定量的に示すには大変困難だろう。此の画像は、三角形とか円とかの単純な形の単純な構成の画像構造ではないからである。
しかし、このブログの絵作りの目的は其のような数学的分析ではなく、
画像として面白いか否かにあって、此の1-2画像は私には確かに面白いのである。