PCが描く奇妙な画像集(数学的万華鏡と生物形態等の世界)

・インタープリタBASICによるフラクタルとカオスの奇妙な画集。

497 Z^s+sinhZ+0.5画像の s による変容画像(その1)

2014-08-20 06:44:09 | ジュリィア集合の変形：f(Z)+g(Z)+C
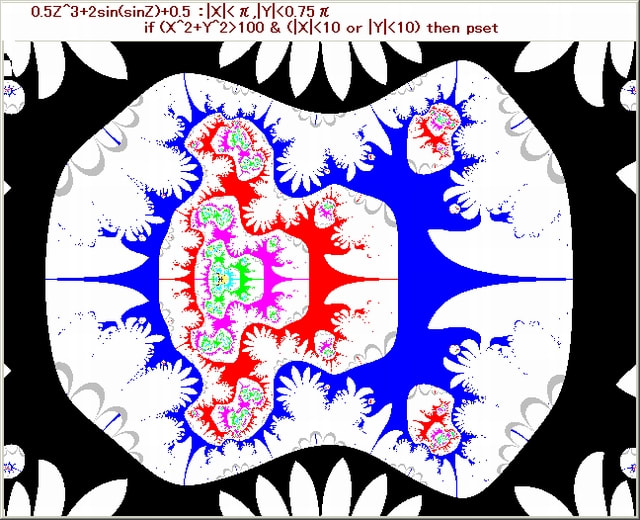
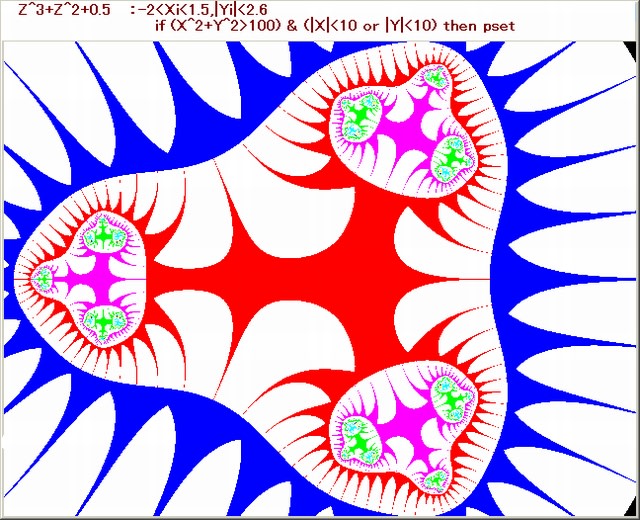
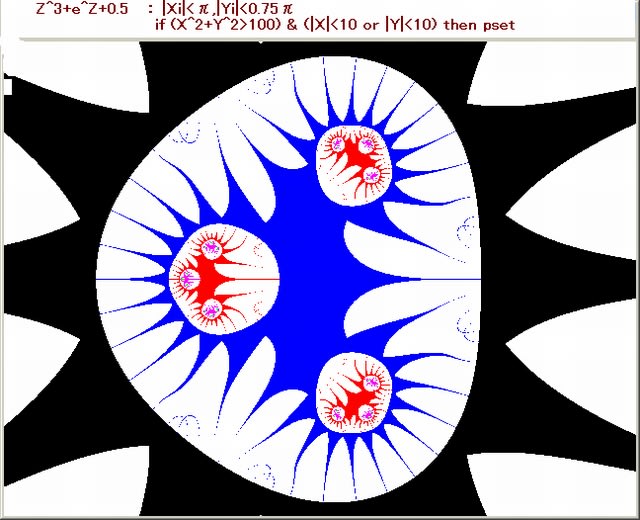
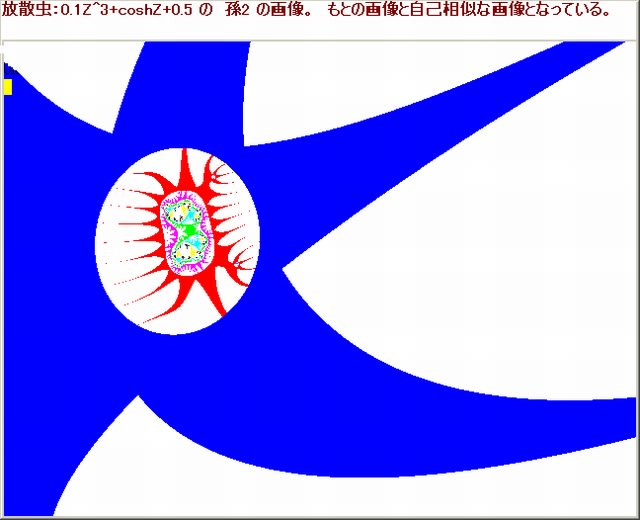
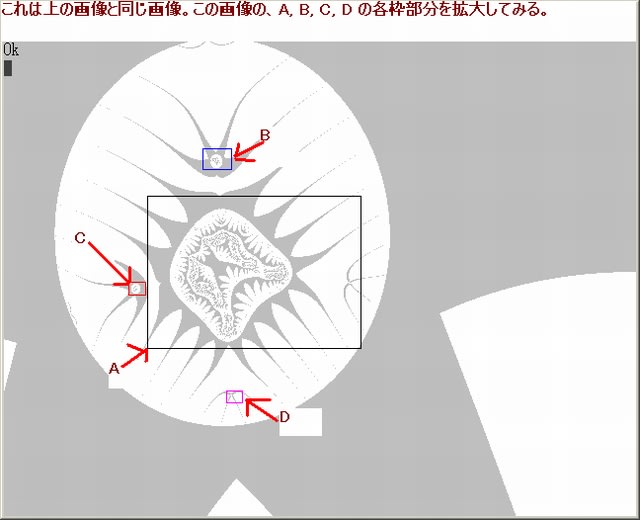
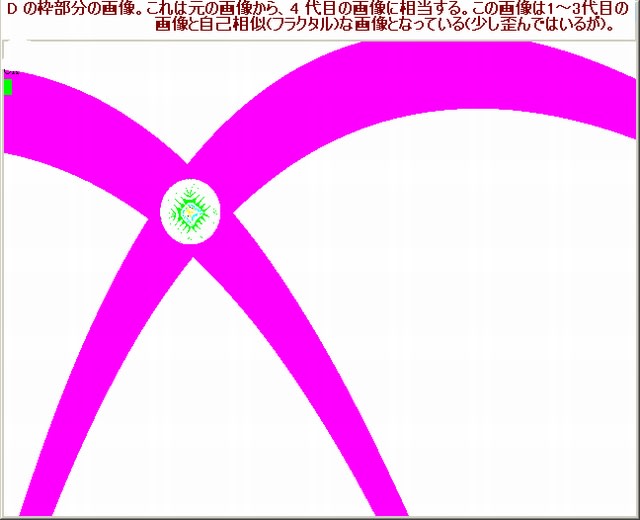
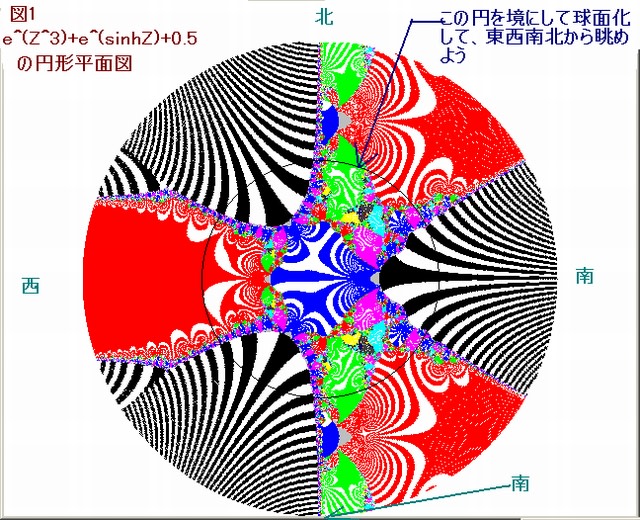
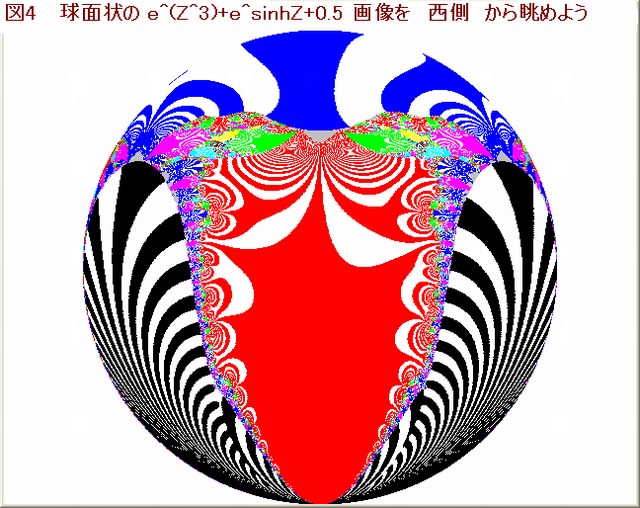
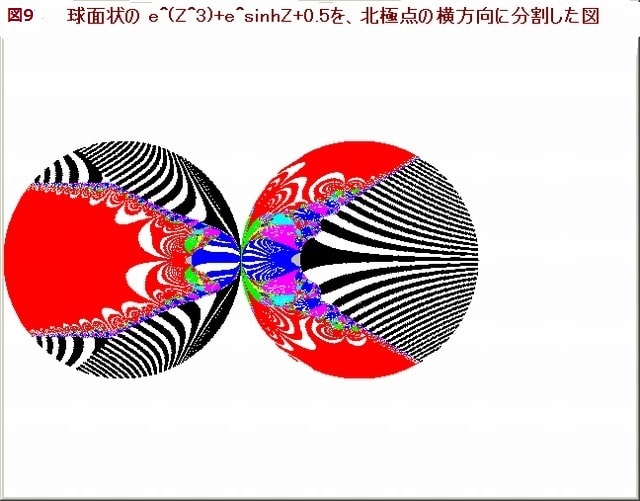
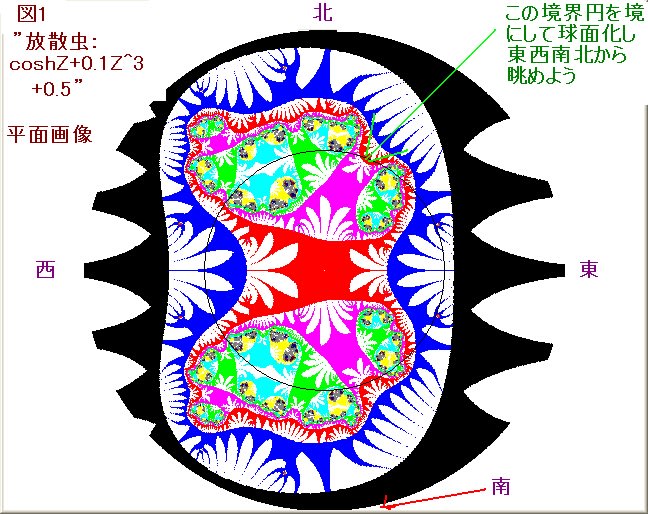
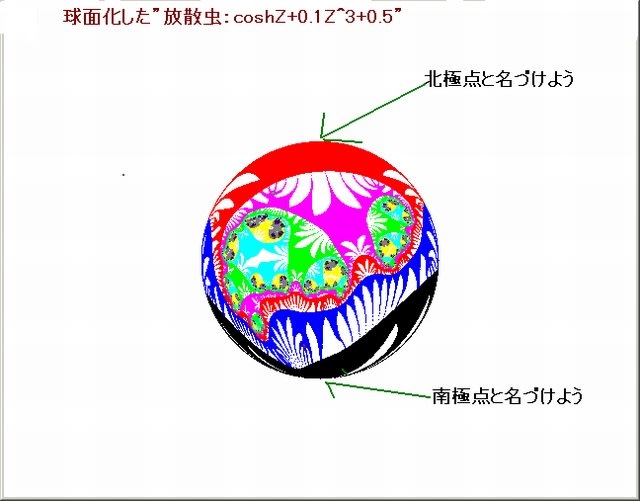
今回の画像は複素関数が、Z^s+sinhZ+0.5 のとき、s を 2→13 にしたときの画像の変容を調べる。

この画像の作成条件は以下のとおり。
1.複素関数：Z^s+sinhZ+0.5,s=2, 3,4,5,6,7,8,9,10,11,12,13
2.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。






141 放散虫：Z^5+sinZ+1.1 画像の自己相似性

2014-07-08 11:27:19 | ジュリィア集合の変形：f(Z)+g(Z)+C
今回は、放散虫：Z今^5+sinZ+1.1 画像について調べる。
下図は、放散虫：Z^5+sinZ+1.1画像の外観図である。



下図は放散虫：Z^5+sinZ+1.1 の”内臓”部の画像である。



上図の放散虫：Z^5+sinZ+1.1 の”内臓”部の一部を徐々に拡大していく。
徐々に拡大する画像を下図に示すように、もとの図(上図)→子→孫→ひ孫→”やしゃこ”と名づけ拡大していく。

















--------------------------------------------------------------------

上図から分かるように、子,孫,ひ孫,及び”やしゃこ”の各画像は、前回の記事(140)の画像と同様に自己相似な画像となっている。この自己相似性は更に拡大していっても存在し続けるだろう。

勿論この性質は此のブログの画像で何度でも現れてきたもので此の性質は画像プログラムのN-loopに拠る性質である。つまり自己回帰という性質である。

140 放散虫：sinZ+sinhZ+0.5 画像の自己相似性

2014-07-08 11:05:41 | ジュリィア集合の変形：f(Z)+g(Z)+C
今回は放散虫：sinZ+sinhZ+0.5 画像について調べる。

下図が放散虫：sinZ+sinhZ+0.5画像の外観図である。
この画像の隅に存在する”つばめ”状のモノの中に在る画像を徐々に拡大してみる。
もとの図(下図)→子→孫→ひ孫→”やしゃこ” のように拡大していく。

ひ孫の画像での”つばめ”部分は画像の分解能の不足のため認識できないため全体を拡大する。





















上図から分かるように子,孫,ひ孫,及び”やしゃこ”の各画像は前回の記事(139)の画像と同様に自己相似な画像となっている。この自己相似性は更に拡大していっても存在し続けるだろう。

勿論この性質は此のブログの画像で何度でも現れてきたもので此の性質は画像プログラムのN-loopに拠る性質である。つまり自己回帰という性質である。

139 放散虫：0.1Z^3+coshZ+0.5 画像の自己相似性：自己回帰性の不思議

2014-07-08 10:30:25 | ジュリィア集合の変形：f(Z)+g(Z)+C
下図がその放散虫：0.1Z^3+coshZ+0.5 画像の外観図である。

この画像の”触手”及び此の”虫”の近くに存在する、つばめ状のモノの中に在る画像を拡大してみる。もとの図(下図)→子1→孫1→ひ孫1 及び、もとの図(下図)→子2→孫2→ひ孫2 のように拡大していく。



























上図から分かるように、子1,孫1,ひ孫1,及び子2,孫2,ひ孫2の各画像は、もとの画像と自己相似な画像となっている。この自己相似性は同様に更に拡大していっても存在し続けるだろう。

勿論この性質は此のブログの画像で何度でも現れてきたもので、この性質は画像プログラムのN-loopに拠る性質である。つまり自己回帰という性質だ。

思えば自己回帰(電子工学でいうところのフィードバック)こそが此のブログの画像を作っているキーワードであり、”創造性”の秘密なのだ。ちょっと神秘的なことだ。其れは何かのメタファーのような気もする。

さて、なんのメタファーでだろうか？

109 sinZ+coshZ+0.5画像のフラクタル性(その3)：結論

2014-07-06 09:45:23 | ジュリィア集合の変形：f(Z)+g(Z)+C
記事107よりsinZ+coshZ+0.5画像のフラクタル性について調べてきたが、此処で少し整理してみる。

***

先ずsinZ+coshZ+0.5画像の出発点の画像を記事107の一番上の画像とし其れを1代目画像と名づける。 その記事の画像の中の4箇所の部分画像を2代目画像と名づける。記事107の掲載画像から分かるように、1代目と2代目画像とには歪んではいるが、自己相似(フラクタル)性があった。

記事108では、1代目の4箇所の部分画像の一つである C 枠部分の画像(2代目画像の一つ)の中の、4箇所の部分の画像を、それぞれ拡大した。それらの各拡大画像を3代目画像と名づける。
それらの3代目画像と2代目画像とには歪んではいるが相似(フラクタル)な画像で構成されていた。

従って、3代目画像と1代目画像とには歪んではいるが、相似(フラクタル)な画像で構成されていることが分かる。

では、4代目の画像は、どうなるか？　それが下図以下に示した画像である。
下図は前記事108の C 枠部分(3代目画像の一つ)の画像である。其の3代目画像の中の4箇所の部分(これらは4代目画像となる)を拡大してみる。
-----------------------------------------------------












-----------------------------------------------------
上図から分かるように、A, B, C, D の枠部分の各画像・・・4代目画像に相当するが・・・それらの各画像は、少し歪んでいるにせよ、3代目の画像と自己相似(フラクタル)な画像となっている。

従って、4代目画像は、1～3代目画像と少し歪んでいるにせよ自己相似(フラクタル)な画像となっていることになる。

***

結局、記事107から行ってきたことにより分かることは、このsinZ+coshZ+0.5 画像は、(歪んではいるが)相似な部分画像から構成されており、更に其の部分画像自身も、(歪んではいるが)相似な部分画像から構成されている、ということを示している。

この全体と部分の自己相似(フラクタル)性の連鎖は、おそらく無限に続いていると思われる。

此れは奇妙というか不思議というか大変面白い画像構成である。

此の画像構成の正体は勿論画像作成プログラム(アルゴリズム)でのN-loopに有る。つまり自己回帰性である。　此の自己回帰性が無限に続く限り、その投影である画像も永遠に自己相似性を続けていく、ということだろう。

088 放散虫：sinZ+Z^2+0.5” の変形

2014-07-04 13:49:56 | ジュリィア集合の変形：f(Z)+g(Z)+C
下図の作成条件は以下のとおり。

1.複素関数：sinZ+Z^2+0.5
2.N-loop脱出条件：X^2+Y^2＞100
3. pset条件：sinX＞sinY



下図は上図の作成どき複素関数の虚数部の与え方を間違えたときの画像である。
これはこれで面白い画像なので掲載する。間違えたのは虚数部を与える式を
Y=FNSINI(X1,Y)+FNI2(X1,Y)とすべきところを、Y=FNSINI(X1,Y)+FNI2(X,Y)
としてしまったのだ。
このように虚数部を間違えた式が一体どんな複素関数になるのか見当もつかないが、
この複素関数も此のブログでは間違ったものではない。
このブログでの複素関数は「なんでもOK」だからだ。