記事652掲載した画像を赤黒縞模様化し画像を単純にすることによって、
それらの画像構造の共通性を明確化する。
先ず記事652掲載画像を再掲する。
下図の画像の作成条件は、以下のとおり。
1. 複素関数:(sinZ)(e^sinZ)+1 。
2. N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>10 or |Q|<0.1)
3. pset条件:|X|<10 or |Y|<10
4. 色設定:N-loop貫通時はC=15。N-loop脱出時は其の時のNをNoとすると C=No mod 16,C=7→8
5. Nmax=500
6. N-loop入力範囲は、-1.5π<Xi<0.5π,|Yi|<0.75π
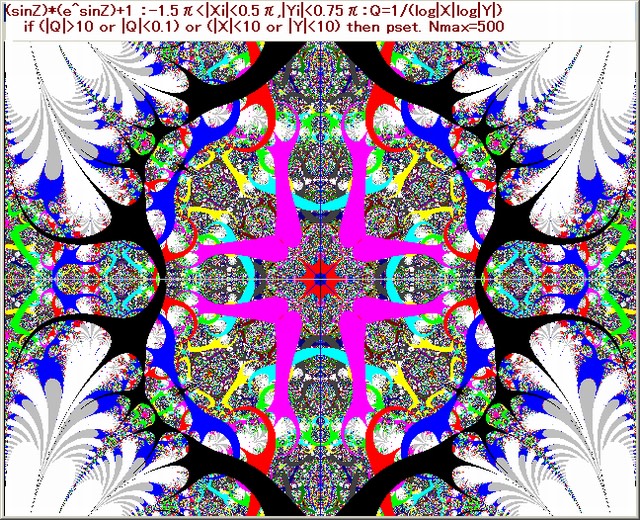
上図の中の 10 箇所を選び、それらを拡大する。拡大の部分も下図に示す。


--------------------------------------------------------










------------------------------------------------------
上図の各拡大画像は、似たような画像構造になっていることが分かる。
しかし、色:C=No mod 16 として16進の色構造となっていると同時に
画像の細部まで描いているため、それらの画像構造の共通性が判別しにくい。
そのため、以下のように各画像を単純化する。
N-loop脱出時のNをNoとする。
(1)No=偶数の場合には色:C=0(赤)とする。
(2)No=奇数の場合には色:C=2(黒)とする。
(3)Naを適当な値としたとき、No<=Naの場合のみ画像表示する。
下図に上記した赤黒縞模様化した画像を示す。
下図から分かるように各画像は似た画像構造となっていることが分かる。
全く同一な画像ではないが互いに自己相似な画像となっている。











それらの画像構造の共通性を明確化する。
先ず記事652掲載画像を再掲する。
下図の画像の作成条件は、以下のとおり。
1. 複素関数:(sinZ)(e^sinZ)+1 。
2. N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>10 or |Q|<0.1)
3. pset条件:|X|<10 or |Y|<10
4. 色設定:N-loop貫通時はC=15。N-loop脱出時は其の時のNをNoとすると C=No mod 16,C=7→8
5. Nmax=500
6. N-loop入力範囲は、-1.5π<Xi<0.5π,|Yi|<0.75π

上図の中の 10 箇所を選び、それらを拡大する。拡大の部分も下図に示す。


--------------------------------------------------------










------------------------------------------------------
上図の各拡大画像は、似たような画像構造になっていることが分かる。
しかし、色:C=No mod 16 として16進の色構造となっていると同時に
画像の細部まで描いているため、それらの画像構造の共通性が判別しにくい。
そのため、以下のように各画像を単純化する。
N-loop脱出時のNをNoとする。
(1)No=偶数の場合には色:C=0(赤)とする。
(2)No=奇数の場合には色:C=2(黒)とする。
(3)Naを適当な値としたとき、No<=Naの場合のみ画像表示する。
下図に上記した赤黒縞模様化した画像を示す。
下図から分かるように各画像は似た画像構造となっていることが分かる。
全く同一な画像ではないが互いに自己相似な画像となっている。




















