記事107よりsinZ+coshZ+0.5画像のフラクタル性について調べてきたが、此処で少し整理してみる。
***
先ずsinZ+coshZ+0.5画像の出発点の画像を記事107の一番上の画像とし其れを1代目画像と名づける。 その記事の画像の中の4箇所の部分画像を2代目画像と名づける。記事107の掲載画像から分かるように、1代目と2代目画像とには歪んではいるが、自己相似(フラクタル)性があった。
記事108では、1代目の4箇所の部分画像の一つである C 枠部分の画像(2代目画像の一つ)の中の、4箇所の部分の画像を、それぞれ拡大した。それらの各拡大画像を3代目画像と名づける。
それらの3代目画像と2代目画像とには歪んではいるが相似(フラクタル)な画像で構成されていた。
従って、3代目画像と1代目画像とには歪んではいるが、相似(フラクタル)な画像で構成されていることが分かる。
では、4代目の画像は、どうなるか? それが下図以下に示した画像である。
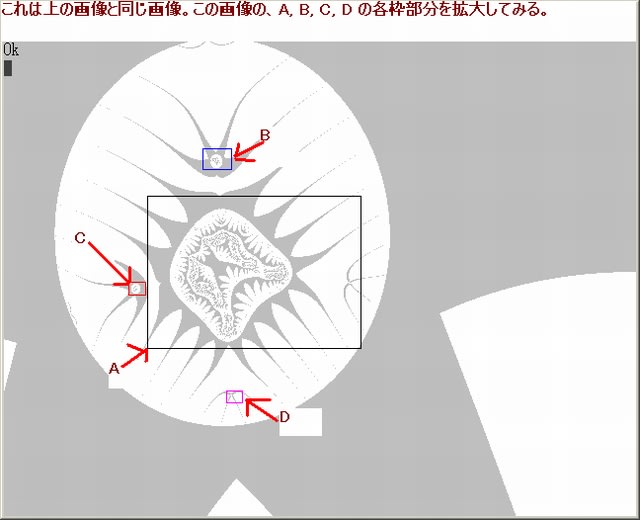
下図は前記事108の C 枠部分(3代目画像の一つ)の画像である。其の3代目画像の中の4箇所の部分(これらは4代目画像となる)を拡大してみる。
-----------------------------------------------------




-----------------------------------------------------
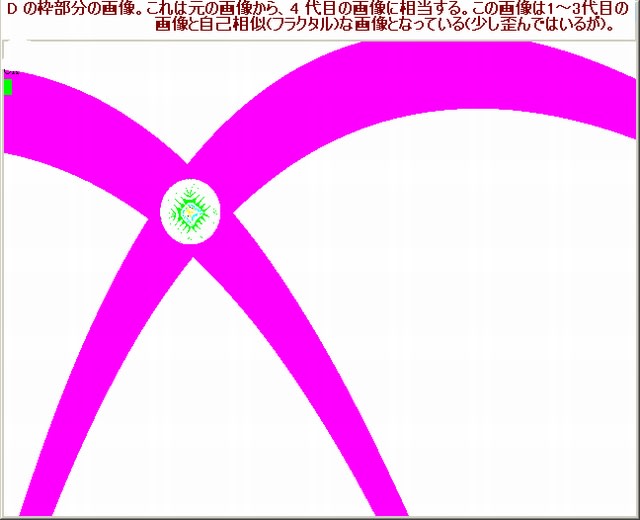
上図から分かるように、A, B, C, D の枠部分の各画像・・・4代目画像に相当するが・・・それらの各画像は、少し歪んでいるにせよ、3代目の画像と自己相似(フラクタル)な画像となっている。
従って、4代目画像は、1~3代目画像と少し歪んでいるにせよ自己相似(フラクタル)な画像となっていることになる。
***
結局、記事107から行ってきたことにより分かることは、このsinZ+coshZ+0.5 画像は、(歪んではいるが)相似な部分画像から構成されており、更に其の部分画像自身も、(歪んではいるが)相似な部分画像から構成されている、ということを示している。
この全体と部分の自己相似(フラクタル)性の連鎖は、おそらく無限に続いていると思われる。
此れは奇妙というか不思議というか大変面白い画像構成である。
此の画像構成の正体は勿論画像作成プログラム(アルゴリズム)でのN-loopに有る。つまり自己回帰性である。 此の自己回帰性が無限に続く限り、その投影である画像も永遠に自己相似性を続けていく、ということだろう。
***
先ずsinZ+coshZ+0.5画像の出発点の画像を記事107の一番上の画像とし其れを1代目画像と名づける。 その記事の画像の中の4箇所の部分画像を2代目画像と名づける。記事107の掲載画像から分かるように、1代目と2代目画像とには歪んではいるが、自己相似(フラクタル)性があった。
記事108では、1代目の4箇所の部分画像の一つである C 枠部分の画像(2代目画像の一つ)の中の、4箇所の部分の画像を、それぞれ拡大した。それらの各拡大画像を3代目画像と名づける。
それらの3代目画像と2代目画像とには歪んではいるが相似(フラクタル)な画像で構成されていた。
従って、3代目画像と1代目画像とには歪んではいるが、相似(フラクタル)な画像で構成されていることが分かる。
では、4代目の画像は、どうなるか? それが下図以下に示した画像である。
下図は前記事108の C 枠部分(3代目画像の一つ)の画像である。其の3代目画像の中の4箇所の部分(これらは4代目画像となる)を拡大してみる。
-----------------------------------------------------






-----------------------------------------------------
上図から分かるように、A, B, C, D の枠部分の各画像・・・4代目画像に相当するが・・・それらの各画像は、少し歪んでいるにせよ、3代目の画像と自己相似(フラクタル)な画像となっている。
従って、4代目画像は、1~3代目画像と少し歪んでいるにせよ自己相似(フラクタル)な画像となっていることになる。
***
結局、記事107から行ってきたことにより分かることは、このsinZ+coshZ+0.5 画像は、(歪んではいるが)相似な部分画像から構成されており、更に其の部分画像自身も、(歪んではいるが)相似な部分画像から構成されている、ということを示している。
この全体と部分の自己相似(フラクタル)性の連鎖は、おそらく無限に続いていると思われる。
此れは奇妙というか不思議というか大変面白い画像構成である。
此の画像構成の正体は勿論画像作成プログラム(アルゴリズム)でのN-loopに有る。つまり自己回帰性である。 此の自己回帰性が無限に続く限り、その投影である画像も永遠に自己相似性を続けていく、ということだろう。



















