前記事では、Z^2+0.5→Z^3+0.5の変容を動画にした。
動画では其の変容の様態は全貌として分かるが詳細な変化は画像として見たほうが
面白い点が多々ある。ということで以後、静止画像でいろいろと調べてみる。
今回の画像はZ^2+0.5画像がZ^3+0.5へ移行する場合の形態の変容を調べるのだが
複素関数:Z^s+0.5において、s=2→2.2→2.→2.6→2.8→3 の画像を調べる。
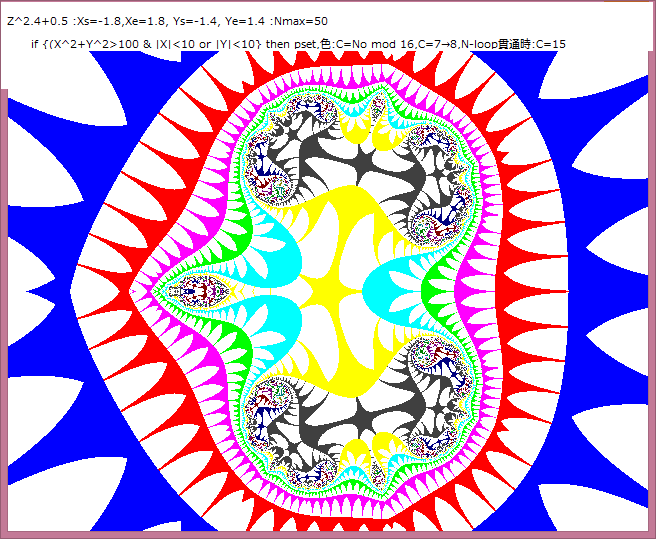
以下の画像から分かるように、Z^s+0.5のsが大きくなるに従い、変化が目立つのは
「放散虫」の「内臓」部分の左端の部分が「成長」していくことである。
また画像の上下の部分も分裂していくことが分かる。
最終的には、二つの自己相似部分が三つの自己相似部分に分裂している。
また其れらの分裂部分自体も、それぞれ相似な部分からなるフラクタル構造となっている。
s=3の場合、即ち Z^3+0.5 画像の此のフラクタル構造に詳細については記事012~023を参照。
この画像の作成条件は以下のとおり。
1.複素関数:Z^s+0.5,s=2, 2.2, 2.4, 2.6, 2.8, 3
2.N-loop脱出条件:X^2+Y^2>100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件:(|X|<10 or |Y|<10) ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。
<img src="https://blogimg.goo.ne.jp/user_image/70/49/ae2660cd3d8d6f4650e5bf84b20fe4cc.png" border="0">






動画では其の変容の様態は全貌として分かるが詳細な変化は画像として見たほうが
面白い点が多々ある。ということで以後、静止画像でいろいろと調べてみる。
今回の画像はZ^2+0.5画像がZ^3+0.5へ移行する場合の形態の変容を調べるのだが
複素関数:Z^s+0.5において、s=2→2.2→2.→2.6→2.8→3 の画像を調べる。
以下の画像から分かるように、Z^s+0.5のsが大きくなるに従い、変化が目立つのは
「放散虫」の「内臓」部分の左端の部分が「成長」していくことである。
また画像の上下の部分も分裂していくことが分かる。
最終的には、二つの自己相似部分が三つの自己相似部分に分裂している。
また其れらの分裂部分自体も、それぞれ相似な部分からなるフラクタル構造となっている。
s=3の場合、即ち Z^3+0.5 画像の此のフラクタル構造に詳細については記事012~023を参照。
この画像の作成条件は以下のとおり。
1.複素関数:Z^s+0.5,s=2, 2.2, 2.4, 2.6, 2.8, 3
2.N-loop脱出条件:X^2+Y^2>100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件:(|X|<10 or |Y|<10) ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。
<img src="https://blogimg.goo.ne.jp/user_image/70/49/ae2660cd3d8d6f4650e5bf84b20fe4cc.png" border="0">


























