(A)・ジュリィア集合変形画像とマンデルブロー画像の以下のように此のブログでは定義する。
・ジュリィア集合変形画像の定義
『ある任意の複素関数をf(Z)+Cとします。Cは実数でも虚数でも構いません。
ある複素画面領域の点(Z=X+iY)において、01.図~04.図の計算手順を満足したとき、その点に色を付けて、その点Zを表示する。この手順を複素画面領域全てについて行い画像を完成させる。』
これとは少し異なる手順の画像作成条件を考える。便宜上、そのような画像をマンデルブロ画像と名づける。この画像作成方法は以下のとおりとする。
・マンデルブロー画像の定義
『ある任意の複素関数をf(Z)+Cとします。Cは複素数でRe.C=CX,Im.C=CYとする。
ある複素画面領域の点(CX,CY)において、Z=X+iYとしてf(Z)+Cを上のフロー図のように計算を行います。この計算手順を満足したとき点(CX,CY)に色をつけて表示する。
この手順をCの複素画面領域全てについて行い画像を完成させる。』
注:複素関数をf(Z)+Cとしたとき、『ジュリィア集合変形画像』の複素画面表示はZ=X+iYで点(X,Y)の集合であり、『マンデルブロー画像は点(CX,CY)の集合』である。
----------------------------------------------------------------------
(B)ジュリィア集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。
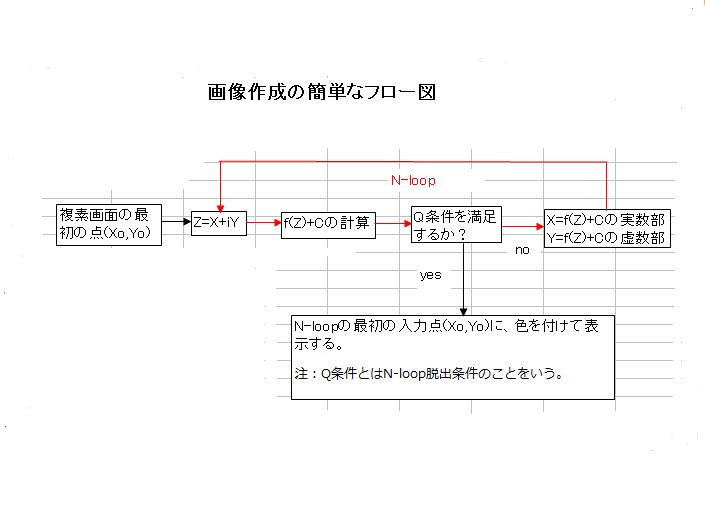
なお極座標を用いた画像作成については下記の2.及び3.を適宜、使用しているが詳細説明は割愛する。
以下此のブログでのジュリィア集合変形画像作成の詳細なプログラム・フロー図を示しておく。
1.方法1:ジュリィア集合変形画像作成のフロー図。
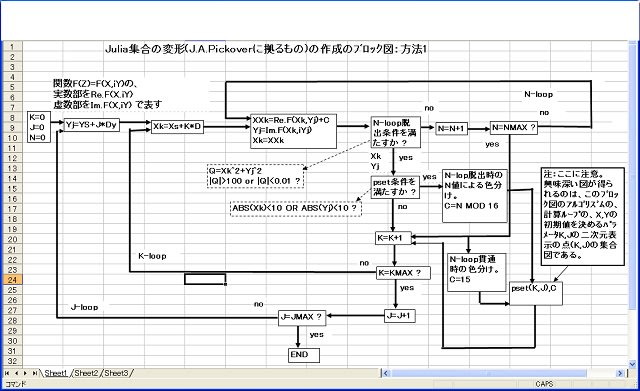
2.方法2:ジュリィア集合変形画像作成のフロー図。(極座標によるもの:1)

3.方法3:ジュリィア集合変形画像作成のフロー図。(極座標によるもの:2)
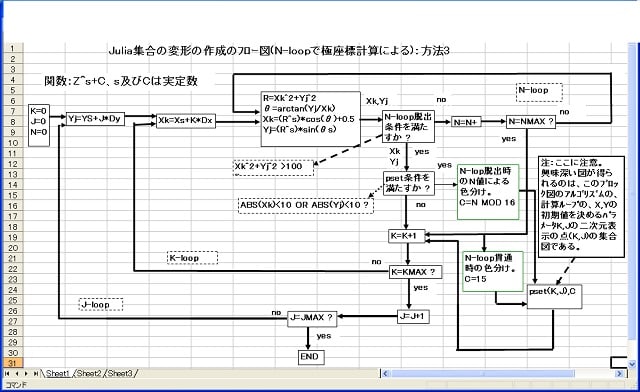
--------------------------------------------------------------------
(C)マンデルブロー集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。

---------------------------------------------------
(D)画像の色の説明を以下に示す。



---------------------------------------------------
(E)N-loop脱出時のNoのLOG化について。
4 N-loop脱出時のNoのLOG化について。
以下においてLOGの底はeである。
BASIC/98において使用できるのは最大16色であり、その色は、O~15の中の整数(Cとする)
で指定される。その具体的な配色は上記(D)項のように決められている。
従って、このブログでは、N-loop脱出時のNをNoとしたとき、Noを色Cで表現する場合、
No>16では、C=No MOD 16として、16進法で゛色を決めている。
マンデルブロ画像のように画像構造が細密な個所では、Noが複雑に変化し、その結果、そのような個所で色が複雑に変化して分かりにくくなる。
そのような場合の画像構造を、より分かりやすくするために、NoをLOG化することが考えられる。 以下、NoをLOG化した場合の検討である。
***
LOG(No)が、1 だけ変化変化した場合(即ち、色Cが次の色に変化した場合)、
Noは、どれだけ変化するのだろうか?
いま、Noの値としてNa,Nbを考え、LOG(Nb)-LOG(Na)=1 とする。
従って、LOG(Nb/Na)=1 故に、Nb/Na=e=2.72 故に Nb=2.72Na となる。
従って、LOG(No)が、1 だけ変化した場合、Noは 2.72 変化していることになる。
逆に言うと、Noが2.72倍変化したとき、色Cが次の色に変わり、画像の色変化が緩和され、
色のよるが画像構造が容易になる(但し、それだけ色による構造分析は粗くなる)
BASIC/98の色配色(整数:Cに対する色の配色)は、画像構造の解析において適当とは言えず、配色を移動させたほうがよい場合がある。
その場合に、Noに適当な係数を掛け配色を移動させる。
例えば、その係数を10^6とすると、
LOG(10^6*No)=LOG(10^6)+LOG(No)=6*LOG(10)+LOG(No)=13.8+LOG(No)
となり、13.8→13 or 12 だけ配色が移動する。
注:配色移動は、C=(適当な整数+LOG(No) としてもよいが、Noに直接、適当な係数を掛けたほうが精度が上がるから上記の方法にした。
***
{ 要約と要点 }
『複素平面上の画像において、このブログでは、Noを色Cで表現している。
マンデルブロ画像のように、画像のある個所においては画像が細密になり(即ち、Noの変化が
細密になり)、Noの表現である色Cの区別が識別しにくくなる。
そのために、NoをLOG(No)で表現する。
そうすることによって、N=2.72*Noになったとき次の色に変わる。
例:No=2(C=2:赤)のとき、N=2.72*2=5.44→5になったとき、次の色:C=3(紫)に変わる。
この場合は、N=2~4はC=2(赤)として単一表現され画像の色の変化が単純化される。
また、単純化されるNの値の数はNに依存し、N→大程大きくなる。
最大となるのは、No MOD 16=15 のときで、15*2.72=40.8→40 となりNoの変化が40でも同一色で表示され、画像解析が容易となる。
この色の単純化(グループ化)は、実際には、Noの係数(例:10^6)を含めてのLOG化と色の16進法化で行われるから、これ自体が複雑な操作であるが、LOG(No)化によって画像の色による解析が容易になることは確かである。但し、その分、解析は粗くはなる。
・ジュリィア集合変形画像の定義
『ある任意の複素関数をf(Z)+Cとします。Cは実数でも虚数でも構いません。
ある複素画面領域の点(Z=X+iY)において、01.図~04.図の計算手順を満足したとき、その点に色を付けて、その点Zを表示する。この手順を複素画面領域全てについて行い画像を完成させる。』
これとは少し異なる手順の画像作成条件を考える。便宜上、そのような画像をマンデルブロ画像と名づける。この画像作成方法は以下のとおりとする。
・マンデルブロー画像の定義
『ある任意の複素関数をf(Z)+Cとします。Cは複素数でRe.C=CX,Im.C=CYとする。
ある複素画面領域の点(CX,CY)において、Z=X+iYとしてf(Z)+Cを上のフロー図のように計算を行います。この計算手順を満足したとき点(CX,CY)に色をつけて表示する。
この手順をCの複素画面領域全てについて行い画像を完成させる。』
注:複素関数をf(Z)+Cとしたとき、『ジュリィア集合変形画像』の複素画面表示はZ=X+iYで点(X,Y)の集合であり、『マンデルブロー画像は点(CX,CY)の集合』である。
----------------------------------------------------------------------
(B)ジュリィア集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。

なお極座標を用いた画像作成については下記の2.及び3.を適宜、使用しているが詳細説明は割愛する。
以下此のブログでのジュリィア集合変形画像作成の詳細なプログラム・フロー図を示しておく。
1.方法1:ジュリィア集合変形画像作成のフロー図。

2.方法2:ジュリィア集合変形画像作成のフロー図。(極座標によるもの:1)

3.方法3:ジュリィア集合変形画像作成のフロー図。(極座標によるもの:2)

--------------------------------------------------------------------
(C)マンデルブロー集合変形画像の作成手順のプログラム・概略フロー図を以下に示す。

---------------------------------------------------
(D)画像の色の説明を以下に示す。



---------------------------------------------------
(E)N-loop脱出時のNoのLOG化について。
4 N-loop脱出時のNoのLOG化について。
以下においてLOGの底はeである。
BASIC/98において使用できるのは最大16色であり、その色は、O~15の中の整数(Cとする)
で指定される。その具体的な配色は上記(D)項のように決められている。
従って、このブログでは、N-loop脱出時のNをNoとしたとき、Noを色Cで表現する場合、
No>16では、C=No MOD 16として、16進法で゛色を決めている。
マンデルブロ画像のように画像構造が細密な個所では、Noが複雑に変化し、その結果、そのような個所で色が複雑に変化して分かりにくくなる。
そのような場合の画像構造を、より分かりやすくするために、NoをLOG化することが考えられる。 以下、NoをLOG化した場合の検討である。
***
LOG(No)が、1 だけ変化変化した場合(即ち、色Cが次の色に変化した場合)、
Noは、どれだけ変化するのだろうか?
いま、Noの値としてNa,Nbを考え、LOG(Nb)-LOG(Na)=1 とする。
従って、LOG(Nb/Na)=1 故に、Nb/Na=e=2.72 故に Nb=2.72Na となる。
従って、LOG(No)が、1 だけ変化した場合、Noは 2.72 変化していることになる。
逆に言うと、Noが2.72倍変化したとき、色Cが次の色に変わり、画像の色変化が緩和され、
色のよるが画像構造が容易になる(但し、それだけ色による構造分析は粗くなる)
BASIC/98の色配色(整数:Cに対する色の配色)は、画像構造の解析において適当とは言えず、配色を移動させたほうがよい場合がある。
その場合に、Noに適当な係数を掛け配色を移動させる。
例えば、その係数を10^6とすると、
LOG(10^6*No)=LOG(10^6)+LOG(No)=6*LOG(10)+LOG(No)=13.8+LOG(No)
となり、13.8→13 or 12 だけ配色が移動する。
注:配色移動は、C=(適当な整数+LOG(No) としてもよいが、Noに直接、適当な係数を掛けたほうが精度が上がるから上記の方法にした。
***
{ 要約と要点 }
『複素平面上の画像において、このブログでは、Noを色Cで表現している。
マンデルブロ画像のように、画像のある個所においては画像が細密になり(即ち、Noの変化が
細密になり)、Noの表現である色Cの区別が識別しにくくなる。
そのために、NoをLOG(No)で表現する。
そうすることによって、N=2.72*Noになったとき次の色に変わる。
例:No=2(C=2:赤)のとき、N=2.72*2=5.44→5になったとき、次の色:C=3(紫)に変わる。
この場合は、N=2~4はC=2(赤)として単一表現され画像の色の変化が単純化される。
また、単純化されるNの値の数はNに依存し、N→大程大きくなる。
最大となるのは、No MOD 16=15 のときで、15*2.72=40.8→40 となりNoの変化が40でも同一色で表示され、画像解析が容易となる。
この色の単純化(グループ化)は、実際には、Noの係数(例:10^6)を含めてのLOG化と色の16進法化で行われるから、これ自体が複雑な操作であるが、LOG(No)化によって画像の色による解析が容易になることは確かである。但し、その分、解析は粗くはなる。



















