前記事302では、N-loopの点(X,Y)と表示座標領域:D の中心点(-1.5,0)との距離:R
の挙動を調べた。詳細な説明は前記事302の説明を参照。
***
今回は、距離:R の挙動ではなく、N-loopの点(X,Y)そのものの挙動を調べる。
前記事で説明したように、X,Yはパラメータ:K1,J1を、前記事の(3)or(4)式のように
すれば、その挙動をPC表示座標点(K1,J1)に変換して調べることができる。
前記事の該当部分を以下に再掲する。
***
『点(X,Y)に相当するPCの表示座標を点(K1,Y1)とする。
ここで、X=CXS+DX*K1, Y=CYS+DY*J1・・・・・・・・・・・・・・・・・・・・・・(3)
とすれば、点(X,Y)の座標は、Dの座標と共通化でき、
K1=(X-CXS)/DX , J1=(Y-CYS)/DY・・・・・・・・・・・・・・・・・・・・・・・・・(4)
として、点(X,Y)と点(K1,J1)は相互変換できる。』
***
今回の記事も、表示座標領域:D は、実軸:-1.5~0.5 虚軸:-1~1とする。
Nmaxも16とする。従って、前回同様に、色:C のcolor code No.が、
点(X,Y)のN-loopの巡回の回数に相当する。
***
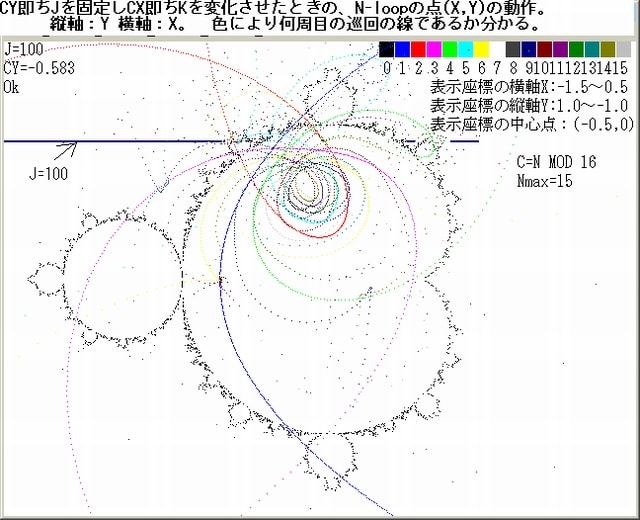
今回も、CY即ちJを固定して、CX即ちKを0→480に移動させ、そのときの
点(X,Y)即ち点(K1,J1)の挙動を調べる。
下図にその挙動を示すが図中にマンデルブロ集合の概略境界線を描いているが、
この境界線と点(X,Y)の座標は一致させている。
従って、マンデルブロ集合と点(X,Y)との関係は直接画像で理解できる。
また以下の図の太い横線は、固定されたCY即ちJを示している。
-----------------------------------------------








----------------------------------------------
上図から分かるように、CY(or J)がマンデルブロ集合内にあると、点(X,Y)の軌跡は
複雑となり、その複雑さは、CY(or J)に強く依存しているが、概略としてみえて
くるのは、、CY(or J)が中央値に近づくにつれて軌跡の形が『平べったく』なって
くることであるが、その形自体は多種多様である。また色からみて、
N-loopの巡回のしかたも決まった規則性は見出されない。
しかし、巡回の回数が増加するにつれて軌跡線が集まってくる箇所(収束)が
あるように見える。しかも、そのような収束箇所は複数の場合もある(J=200の場合)。このような傾向はNmaxを大きくすれば、より鮮明になるかも知れない
の挙動を調べた。詳細な説明は前記事302の説明を参照。
***
今回は、距離:R の挙動ではなく、N-loopの点(X,Y)そのものの挙動を調べる。
前記事で説明したように、X,Yはパラメータ:K1,J1を、前記事の(3)or(4)式のように
すれば、その挙動をPC表示座標点(K1,J1)に変換して調べることができる。
前記事の該当部分を以下に再掲する。
***
『点(X,Y)に相当するPCの表示座標を点(K1,Y1)とする。
ここで、X=CXS+DX*K1, Y=CYS+DY*J1・・・・・・・・・・・・・・・・・・・・・・(3)
とすれば、点(X,Y)の座標は、Dの座標と共通化でき、
K1=(X-CXS)/DX , J1=(Y-CYS)/DY・・・・・・・・・・・・・・・・・・・・・・・・・(4)
として、点(X,Y)と点(K1,J1)は相互変換できる。』
***
今回の記事も、表示座標領域:D は、実軸:-1.5~0.5 虚軸:-1~1とする。
Nmaxも16とする。従って、前回同様に、色:C のcolor code No.が、
点(X,Y)のN-loopの巡回の回数に相当する。
***
今回も、CY即ちJを固定して、CX即ちKを0→480に移動させ、そのときの
点(X,Y)即ち点(K1,J1)の挙動を調べる。
下図にその挙動を示すが図中にマンデルブロ集合の概略境界線を描いているが、
この境界線と点(X,Y)の座標は一致させている。
従って、マンデルブロ集合と点(X,Y)との関係は直接画像で理解できる。
また以下の図の太い横線は、固定されたCY即ちJを示している。
-----------------------------------------------









----------------------------------------------
上図から分かるように、CY(or J)がマンデルブロ集合内にあると、点(X,Y)の軌跡は
複雑となり、その複雑さは、CY(or J)に強く依存しているが、概略としてみえて
くるのは、、CY(or J)が中央値に近づくにつれて軌跡の形が『平べったく』なって
くることであるが、その形自体は多種多様である。また色からみて、
N-loopの巡回のしかたも決まった規則性は見出されない。
しかし、巡回の回数が増加するにつれて軌跡線が集まってくる箇所(収束)が
あるように見える。しかも、そのような収束箇所は複数の場合もある(J=200の場合)。このような傾向はNmaxを大きくすれば、より鮮明になるかも知れない



















