記事274にヴエルンハルスト方程式:X(t+1)=AX(t){1-X(t)} ・・・・・(1)
(ここで、A は定数、X(t)は変数)
画像を掲載した。
これはtの漸化式であるが、X(t)の漸化値が定数Aによって様相が一変することを見た。
A の増加に従い、X(t)の漸化値は、ある固定値から始まり分岐する。
その分岐は更に分岐し続け、あるA値からX(t)の値はカオス状態に突入したのであった。
下図は記事274に掲載した、その様子を示す画像である。

では、ヴエルンハルスト方程式(1)式において、Aを固定して、横軸にtをとり、
縦軸にX(t)にとって、t の変化に対してX(t)はどのように変化するのだろうか?
それを調べたのが下図である。A の代表的に四つの値で見てみよう。
A=2, A=3.3, A=3.5とA=4の場合である。
各場合の画像を以下に示す。



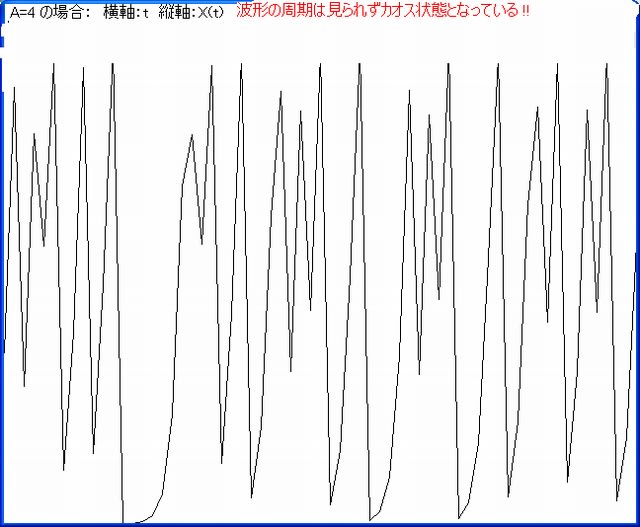
上図から分かるように一番上の画像と、A=2, A=3.3, A=3.5とA=4を固定した t 対 X(t)画像は
一致している。当然のことだが、A=4の場合のX(t)のカオス画像の様子は面白い。
なるほど、X(t)はtに対して予想不可能に見える。
---------------------------------------
追記:
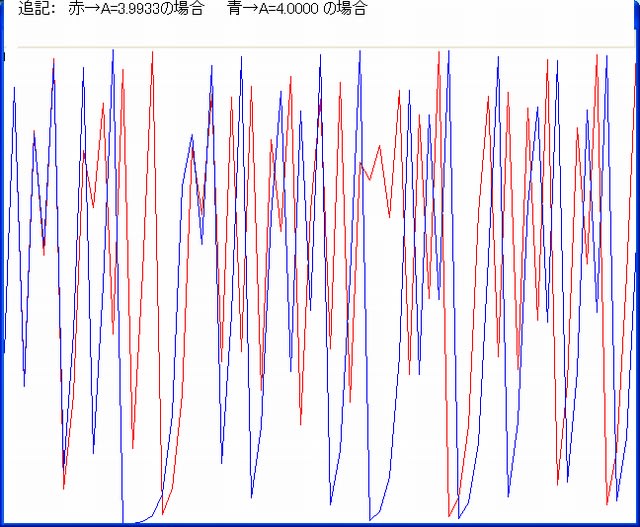
(ここで、A は定数、X(t)は変数)
画像を掲載した。
これはtの漸化式であるが、X(t)の漸化値が定数Aによって様相が一変することを見た。
A の増加に従い、X(t)の漸化値は、ある固定値から始まり分岐する。
その分岐は更に分岐し続け、あるA値からX(t)の値はカオス状態に突入したのであった。
下図は記事274に掲載した、その様子を示す画像である。

では、ヴエルンハルスト方程式(1)式において、Aを固定して、横軸にtをとり、
縦軸にX(t)にとって、t の変化に対してX(t)はどのように変化するのだろうか?
それを調べたのが下図である。A の代表的に四つの値で見てみよう。
A=2, A=3.3, A=3.5とA=4の場合である。
各場合の画像を以下に示す。




上図から分かるように一番上の画像と、A=2, A=3.3, A=3.5とA=4を固定した t 対 X(t)画像は
一致している。当然のことだが、A=4の場合のX(t)のカオス画像の様子は面白い。
なるほど、X(t)はtに対して予想不可能に見える。
---------------------------------------
追記:




















