[2022年7月13日 更新]
結論から言うと、都立高校入試で「球」についての問題は出題されたことがない。
今回はこのお話をする。
◆球について学ぶのは中1と中3
まず中1で球の体積・表面積の求め方を学習する。
円の面積や平行四辺形の面積は、「なぜ、この公式になるのか」を小学校で教えてもらったはずだ。
公式だけを覚え、なぜ平行四辺形の面積は 底辺×高さ なのかを理解していない子は、必ず受験数学でつまづくタイプ。
もし分からなければ、小5の教科書を読めば分かる。自分で調べよう。
それでも分からなければ、以下のサイトの最下段を見ればいい。
<出典:算数の公式>
しかし、球の体積と表面積の公式を導き出す方法は中学校では習えない。
高校数学で判明することになる。しばらくのしんぼうじゃ。
中2では「球」を取り扱わない。
中3になって最後の最後、三平方の定理を学ぶ時に再び「球」が現れる。
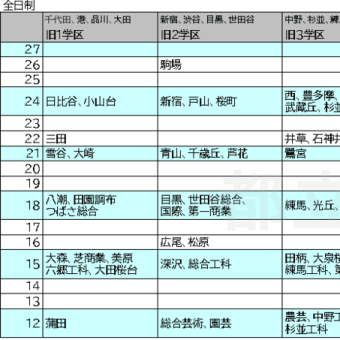
しかし、都立入試では
円錐や円柱ですらめったに出ない。
2011年度、2018年度、2020年度入試の大問2で円柱、2013年度入試の大問2で円錐は出された。
空間図形を扱う大問5でも「球」はまったく出題されていない。
<過去記事:都立高校入試数学の法則<5> 大問5にも規則性あり>
◆そもそも中1で「球」を学ぶ意味はあるか
単元として、中1で空間図形を学ぶ。柱体と錐体の体積・表面積を学ぶついでに、球も学ぶのだろう。
そこで質問。
キミは錐体の体積はなぜ 底面積×高さ×1/3 なのかを教わっただろうか。
教えてもらった、もしくは考える指針を示してくれた先生に出会っていたら、キミはきっと数学を好きになったはず。
中学校の指導では、球の体積・表面積と同様にこの公式の理由は教わらない。
これも厳密には高校数学で学ぶのだが、興味があったら調べてみるといい。
「 錐体 なぜ1/3 」
でググればすぐだ。
◆結論。球の問題は都立入試に出ない
中学校教科書に載っている内容なので、もちろん都立入試で出る可能性はゼロではない。
が、過去問題の傾向から「出やすい問題」は分かっている。そちらから取り組む方が効率がいい。
時間に余裕があるなら、私立高校入試問題から「球」の問題を探してみるといい。
私立の難関校ではちょくちょく出題されている。
点Oを中心とした半径5の球がある。
点Oからの距離が3である平面でこの球を切ったとき、切り口の面積を求めよ。ただし、円周率はπとする。
なお本郷高校の数学入試問題には、図やグラフはいっさい書かれていない。
問題文から推察して、自分で書かねばならない。
これはセンター試験も同じである。大学入試を見すえた入試問題なのだ。
この問題の正答率は63%
本郷の受験生でも4割近くが正答できていない。
図さえ正しく書ければ、30秒で解ける問題だ。
三平方の定理が分かっているのなら、ぜひ解いてみて欲しい。
解答は2019年10月18日に、ひっそりツイート済み。
都立に入る! ツイッター 毎日の更新情報を受け取れます