いきなりOpenFOAM でつまずく

翼の揚力発生の仕組みについてシミュレーションで試してみようということで、下記サイトの内容をなぞれば楽勝と思いきや、やたらつまずいたという記録。

いきなりOpenFOAM (16) | 株式会社ソフトフロー

いきなりOpenFOAM (17) | 株式会社ソフトフロー

落とし穴は、ざっとこんなところ

・財団版とESI版の非互換

・OpenFOAMのバージョン間で非互換

・wls のデフォルトユーザー

・FreeCADのバグ

最初に悩んだのは翼型のデータ。上記サイトでは細かい説明がないが、このサイト(UIUC Airfoil Data Site) にある .datファイル (例えば clarky.dat)をダウンロードして、そのままFreeCADに読み込ませればよい。

次に引っかかったのは、財団版とESI版の違い。OpenFOAMには OpenFOAM財団版とOpenCFD社のESI版 (DEXCSはこちら)があって細かいところで互換性がない。前記のサイトで使っているXSimは財団版前提のスクリプトを生成するためESI版だとそのままではNG。具体的には、財団版のsurfaceFeaturesがESI版ではsurfaceFeatureExtractに変わっていて、受け渡すデータの形式もちょっと異なるようだ。そのことを知らずに、「ＯｐｅｎＦＯＡＭによる熱移動と流れの数値解析 」を参考に用意したDEXCSのバーチャルマシンで実行して、うまくゆかずに悩んだ。素直に財団版に乗り換えることにした。

Windows使いの私はwslに Ubuntu 24.04 LTSを入れ、こちらに財団のOpenFOAM (現在のバージョンはv12) をインストールしたが、これもだめ

XSimはエクスポートのフォーマットとして、OpenFOAM 11 / OpenFOAM 10 / OpenFOAM 9 (非推奨) の選択肢がある。つまり、OpenFOAMのバージョンごとの違いを踏まえて作り分けているということ。そして、OpenFOAM最新版の OpenFOAM 12 はまだサポートしていない。

実際に、XSimでOpenFOAM 11 フォーマットで出力したものをOpenFOAM v12で動かしても、Running foamRun in parallel on ... まで表示が進んでハングする。

簡単に推測できるURLにv11のダウンロードページが残っていて、https://openfoam.org/version/11/ こちらの記載に従えば簡単にOpenFOAM v11がインストールできる。

これで万事解決と思いきや、やはりNG。問題は、wslのユーザーだった。実験に使った環境だとrootユーザーだったのだが、それだと不安全ということでOpenFOAMが自分で止めてしまうようだ。

ターミナルからwslのubuntuに入ると、ubuntuの初回起動時に作ったユーザーとしてログインしているはずなのだが、export/importで作ったせいなのだろうかrootユーザーになってしまう。/etc/wsl.confを編集して別に作った一般ユーザーとしてwslのubuntuに入るようにしたところ、無事にXSimで作ったスクリプトを実行できた。

と言っても結構ドキドキさせられた、./Allrunを走らせるとこのような画面が現れて計算の進捗が表示されるが、この画面で最後までいったあとプロンプトが戻ってくるまでが長くて、ハングしているように見えてしまう。

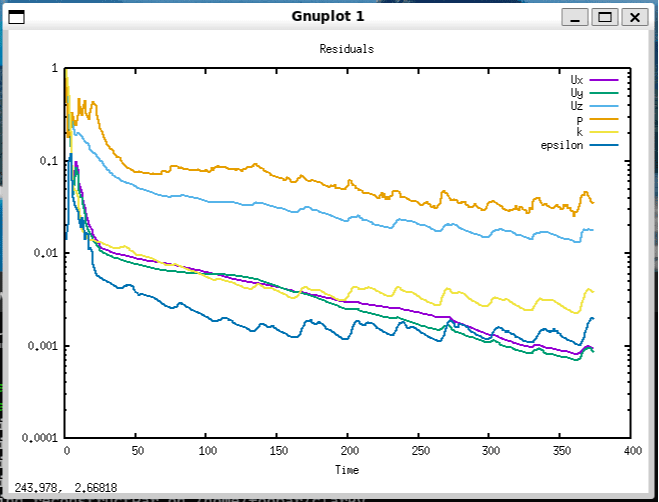
あとは、paraFoamコマンドでParaViewが開いて計算結果を見ることができる。openFoamと一緒にParaViewがインストールされるので世話無し。

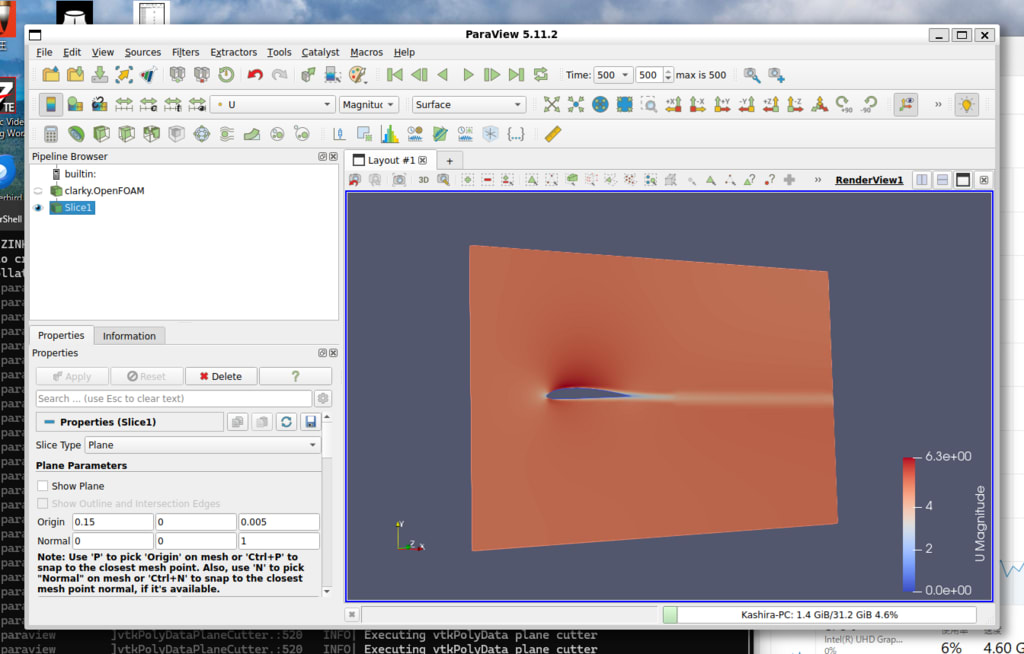
話は前後するが、freeCADでstlデータを作る際にFreeCADの不具合に引っかかった。FreeCAD の現行バージョン( Windows版 0.21.2.33771)で作ったstlファイルをXSimにアップした結果がこちら。風洞部分である直方体のZ軸に伸びる4面の位置がずれている。

しかたないので、FreeCAD 1.0.0 RC2でstlを作りなおしてみたところOK。だが、RC2はGUIが以前とは少し異なるうえ画面表示がだいぶバグっていていまいち。ちなみに、DEXCSのバーチャルマシンにインストールされていたLinux版 FreeCAD 0.20.1 でもこの不具合はなかった。

以上のようにWebにあったチュートリアルを実行するだけで、えらく苦労させられたが、なんとか実行に成功した。やれやれ。

エムデン方程式 - 空気の場合

レーン・エムデン方程式(Lane-Emden equation)を 空気 (2原子分子)について解いてみる。中心が27°, 1気圧 という条件で具体的な数字を出した。
2原子分子なので ɤ = 7/5, N = 5/2. とする。水素の場合と同じようにオイラー法でスプレッドシートを使って数値的に解く。
宇宙空間に水星の質量の半分程度の空気をあつめると自己重力でまとまって、中心は人間が生存できるとなった。だれか験算しておくれ。

エムデン方程式の具体的な形

水素の場合をexcelで計算してグラフに描いた。

球対称で平衡状態にある星(自己重力ガス球)の構造は、密度と圧力の間にポリトロピック関係が成り立つとした場合に次のレーン-エムデン方程式 (Lane-Emden equation) であらわされる。ガス球が水素からできている(単原子理想気体)とするとɤ=5/3 (N=3/2) となる。と、ここまでは、教科書[1]に書いてある話。

では、具体的にはどうなるかを計算してみた。
N=3/2の場合のLane-Emden equationをMaximaを使って変形して、Dの二階微分をDとDの微分であらわすとこうなる。

これをスプレッドシートでオイラー法を使って数値的解くとこんな感じ。より分かりやすく、Dを圧力Pと密度ρに読み替えてみた。


[1] 福江 純・和田桂一・梅村雅之、宇宙流体力学の基礎 (日本評論社、2014)

自己重力等温ガス球の構造

構造が中心に対して球対象だとし、時間的に変化しないとして計算。
星内部に半径方向に微小な円柱を考え、上面と下面の全圧力と円柱内のガスへの重力のつり合いを考えると次の式になる。
(3.29)
また、半径rより内側に含まれる質量Mrは、
(3.31)
さらに、ガスの温度がどこでも一定として、理想気体の状態方程式を当てはめると次の式になる。
(3.46)
ここで、次のような変数変換をする。
(3.47)
(3.48)
すると式はこうなる。[1]
(3.49)
以上 ・・・
いや、これではどんな形状だかさっぱりわからん。
この2階微分方程式は解析的には解けないということなので数値計算する。と言っても、オイラー法ならスプレッドシートでも計算できるので、まずはそれであたりをつけてみる。
まずは、式3.49 を変形して、Dの2階微分 (D")をDの1階微分(D')とDの式 f(D', D)表現する。高校数学のレベルだがチョンボはしたくないので数式処理システム(maxima)に手助けしてもらう。なお、maximaでDと書くと定数扱いされてしまうので、ξの関数 D(ξ) として表現している。

あとは、次の式でξを少しずつ増やしながら計算していけばよい。なお、教科書では、境界条件としてξ=0 の時、D=1で D' = 0と書いてあるが、D"の計算でξ=0は特異点になっているので使えない。まあ、中心付近は重力の効果はほぼ無くて一様だろうから、わずかに離れたところでもD=1でD'=0だとして計算できる。
D (ξ + d) = D(ξ) + d * D'(ξ)
D' (ξ + d) = D'(ξ) + d * D"(ξ)
D" (ξ) = f (D'(ξ + d), D(ξ + d))

ということで計算してみたのだが、どうもDの減少の仕方がが思ったより小さい。グラフにするとこうなる。

青線がDで赤線が1/ξ^2 。D∝1/ξ^2 だとξが増えるに比例して質量Mが増え続けるということなので、どこかが等温ガス球の境界とは言えないということだよね。
定常状態にある理想気体からなる自己重力等温ガス球というのは星とは言えないのかぁ。


[1] 福江 純・和田桂一・梅村雅之、宇宙流体力学の基礎 (日本評論社、2014)

気体の平均分子量の計算

Q. 空気(分子量28のN分子78%, 分子量32のO分子21%, 原子量40のAr 1%)の平均分子量はいくらか.

誤答: 0.78*28 + 0.21*32+0.01*40 ≒ 28.96
正解: 1.0/ ( 0.78/28 + 0.21/32 + 0.01/40) ≒28.84

なぜか？ それは、出題者が78%,21%,1%を重量パーセントとして出題したから。粒子数あるいは体積のパーセントなら最初の式になる。