特異スペクトル変換による変化検知 - その2

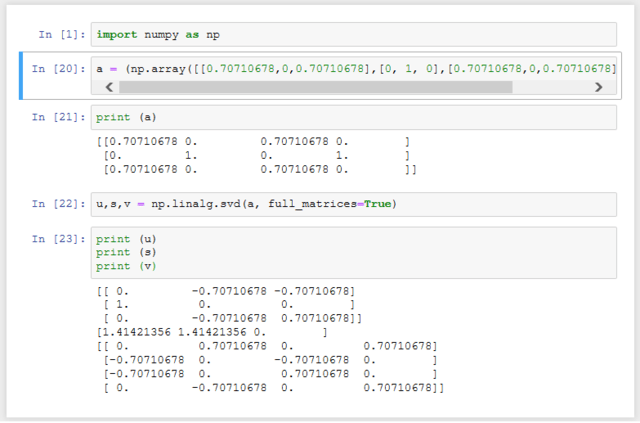
前回の実験で検知できなかった理由はなぜだろうか。

簡単に言うと、特異ベクトルの数に対して特異ベクトルの次元が足りなかったから。計算過程を目視確認しやすいように部分時系列の長さを３としていた。つまり３次元。ここで、二本のベクトルの張る空間は原点を通る平面となる。３次元空間で２つの平面を考えると、どうしても交わることになる。行列２ノルムで考えたとき、２つの平面に３次元空間は狭すぎたということだ。

部分時系列の長さを４に増やして実験した結果は下図のとおり。最初の 11 が顔を出したところまでは変化度 0 だが、11が途中にある間は 0.0078 や 0.00014 といった値を取っていて、変化検知に成功している。

import numpy as np
def normV(v):
    return v / np.linalg.norm(v,2)

pat = [1,0,1,0,1,0,1,0,1,1,0,1,0,1,0,1,0,1,0,1,0,1,0]
M = 4
k=4

c = np.empty((M,0))
for j in range(k):
    c = np.hstack((c, np.array([normV(pat[j:j+M])]).T) )
u1,s1,v1 = np.linalg.svd(c, full_matrices=True)

for i in range (12):
    c = np.empty((M,0))
    for j in range(k):
        c = np.hstack((c, np.array([normV(pat[i+j:i+j+M])]).T) )
    q,s,v = np.linalg.svd(c, full_matrices=True)
    uq = np.dot(u1.T[[0,1],:], q.T[[0,1],:].T)
    print (pat[i:i+M+k-1])
    print ("a = ", 1-np.linalg.norm(uq,2))

[1] 井出 剛、杉山 将, 異常検知と変化検知, 講談社, 2017 ISBN978-4-06-152908-3

特異スペクトル変換による変化検知 - その１

さて、SVDによる特徴パターンの抽出ができたので、本来の目的である変化検知にトライする。

ターゲットは、1,0,1,0,1,0,1,1,0,1,0,1,0　

10の繰り返しの途中で一回引っかかったパターンである。11の所をどのように検知できるか試してみる。
履歴行列も検知行列も、長さ３の部分時系列を４パターンとする。

定常状態は 10の繰り返しなので履歴行列とその左特異ベクトルは最初に計算した固定値を常に用いる。

履歴行列の左特異ベクトルは二つが同位であることを踏まえ、履歴行列と検知行列からおのおの二つの左特異ベクトルを取り出し、行列２ノルムを使って変化度を計算することにした。

まず結果だけ先に示す。



検知行列で見ている範囲に 1 1 が最初に現れたところまでは、変化率が 0.0 だが、あとは 1 1 現れている間ずっと非ゼロになっている。
変化検知ができた...わけではない。値が 1.0e-16 のレベルということは倍精度計算での計算誤差レベル


[1] 井出 剛、杉山 将, 異常検知と変化検知, 講談社, 2017 ISBN978-4-06-152908-3

SVDによる特徴的なパターンの自動抽出 - その3

スライド窓を使って取り出したそれぞれの部分時系列のベクトルは、値そのままではなく長さ１のベクトルに正規化している。

では、正規化しないで生のまま計算したらどうなるだろう。

結果は下図のとおり。左特異ベクトルの上位に [-0.707, 0, -0.707] と [0, 1, 0] が現れるのは同じだが、特異値に差があり前者が√２倍大きい。　1,0,1 も 0,1,0 も同じ回数あるのに前者の特異値が大きいので結果がおかしいことが分かる。

import numpy as np
x = np.array([[1,0,1],[0, 1, 0],[1,0,1],[0,1,0]]).T
print (x)
u1,s1,v1 = np.linalg.svd(x, full_matrices=True)
print (u1)
print (s1)

SVDによる特徴的なパターンの自動抽出 - その2

今回の対象は、101010 という繰り返しパターンだ。

前回、101010 という部分から履歴行列を作って左特異ベクトルをとりだした。

テスト行列はどうなるか。もちろん、たまたま同相 101010 となれば全く同じ左特異ベクトルが得られる。
だが、場合によっては逆相の 010101 となることだってあるだろう。その場合の左特異ベクトルはどうなるだろうか。

numpyで計算した結果は以下のとおり。　



s の最初の２項目が 1.4 なので u の 1列目と2列目が特徴的なパターンということになる。
[0, -1, 0] と [-0.707, 0, -0.707] で符号の違いを別とすれば、履歴行列のものと(計算誤差の範囲で)一致する。


[1] 井出 剛、杉山 将, 異常検知と変化検知, 講談社, 2017 ISBN978-4-06-152908-3

SVDによる特徴的なパターンの自動抽出 - その1

時系列の変化検知手段としての特異スペクトル変換法とやらを試してみる。

おおざっぱに言うと、過去のサンプルの塊と現在のサンプルの塊のそれぞれから、特異値分解による特徴的なパターンを抽出して、過去のそれと現在のそれとの相違を見ようというもの。

まずは、特異値分解を試してみる。

データとしては 1010101 という反復信号を例にとる。窓幅Mを3にとって部分時系列を取得する

例えば、N=４ の部分時系列を取得すると、例えば、[1,0,1], [0 1 0], [1,0,1][, [0,1,0] となる。

これを、フォンミーゼス・フィッシャー分布で扱うためベクトルの長さを 1に規格化すれば、
[0.707, 0, 0.707], [0, 1, 0], [0.707, 0, 0.707], [0, 1, 0] となる。

numpy.linalg.svd で試してみよう。SVDで Xは、部分時系列が列方向なので、ここでは部分時系列を行にして作った配列を転置させて生成する。



s の最初の２項目が 1.4 なので u の 1列目と2列目が特徴的なパターンということになる。
[0, 1, 0] と [-0.707, 0, -0.707] で符号は別とすれば、確かに特徴的なパターンということになる。


[1] 井出 剛、杉山 将, 異常検知と変化検知, 講談社, 2017 ISBN978-4-06-152908-3