3. 実験手法
PMLの性能は、反射波の大きさを剛な境界の場合と比較することで評価する。単純に受音点で音圧を観測した場合、反射が小さい場合に直接波が尾を引く残余と反射波との区別が難しくなることが予想される。そこで、測定時間内には反射波が戻ってこないほど境界の位置を遠のけた場合の測定値を基準として、それとの差を反射波として抽出する。
斜めに音波が入射する場合の性能を評価するため、点音源を用い受音点を3か所設けた。剛な境界の場合、境界に対して音波が垂直に入射し反射して到達する点 P1、およそ45度で入射して反射が到達する点 P2、およそ30度で入射して反射が到達する点 P3 の3点である。音波はいったんPML層の内部に入って反射してくる。PML層が厚くなると厳密には反射角度が異なってくると想定されるが、ここでは無視できるものとして扱う。
具体的には、X 999 cm, Y 599 cm, Z 799 cm の天井以外は剛な境界で囲まれた空間に、下図のように音源と受音点を配置した。Spacial stepは1cm、 time step は 0.01ms。音速cは330m/s、空気密度は1.2047291 kg/m3を使用。CFLは0.33 である。

Fig 3-1 配置図
反射波の大きさには、音圧の絶対値の最大値を使用する。より具体的には、P1では計算開始から11.50msから14.50msまでの3.0ms、P2では16.60msから19.60ms、P3では23.90msから26.90ms の音圧の絶対値の最大値を用いた。
音源は、音源となるセルの音圧を1kHzのsin波で1周期分だけ強制的に与えるという簡便な方法を採用した。
計算は単精度で行った。
4. PMLの層数と反射量
PMLの層数のみを変更し、反射量の関係を調べる。
PMLの層数を8から256まで変え、その他は次の条件で一定とした。Absorption coefficients σには式5を採用し、乗数Mを2, σMAX は 1.0 。音源は、1kHzのsin波1周期。
計算した各受音点での反射波の絶対値のピークを剛な境界の場合を1として現したものが次の図である。

Fig 4-1 PML層数と減衰
Fig.4-1 で示すようにPML層数を指数関数的に増加させることで反射波は指数関数的に減少する。100層あたりで反射波の減少が底を打つが、これはPML層に入射しつつある音圧に対して、単精度浮動小数点の有効桁数(十進で6桁強)では不足するほど反射波の音圧が小さくなりすぎたことにより発生するノイズが卓越するためと考える。
Fig.4-1で興味深い点は、PMLが10層以下であるとPMLへ浅い角度で入射する音波の減衰が特に悪いが、層数を増やすことで顕著に改善される点である。
具体例として、受音点P2における16.6msから19.6msまでの反射波の音圧波形を示す。波形を見やすくするため、音圧のスケールはすべて異なる。青線でしめす剛な境界からの反射波形と比べると、PMLが8層の場合の反射波形はおおむね元の形状をとどめているが、PMLが64層になると反射波形はノイズまみれとなっている。

Fig. 4-2 受音点 P2 での反射波の波形
5. Absorption coefficientsと反射量の関係
Absorption coefficients σに式5を採用した場合、乗数Mとσ max の二つのパラメータとPMLでの反射量の関係を検討する。
fig.5-1は、σmaxを1.0に固定し乗数を1から4まで変えた時の反射量を示す。PMLの層数は16で固定である。

Fig. 5-1
入射角が直角(P1)の場合は乗数が増えるほど反射量が減るが、角度が浅くなるほど反射量が最低となる乗数があることが見える。σ maxが1.0の場合、角度によらない結果を求めた場合では乗数として2が最適で、その場合の反射は1.0E-4以下 (吸収率99.99% 以上) と読み取れる。さらに、σ maxを変えて変えてみる。実は、Absorption coefficents は1.0を超えても吸収層として働く。

Fig. 5-2

Fig. 5-3
fig. 5-2, fig. 5-3は、σ maxを1.2にした場合とσ maxを2.0にした場合の図である。
σ maxを大きくするほど入射角が浅いケースでの反射量が最低となる乗数が増えるとともに、反射量の最低値も減少することが見て取れる。
Fig 5-4は、σ max によって減衰量がどのように変化するかと異なる乗数ごとに追った図である。

Fig. 5-4
角度に因らない結果を求めP1, P2, P3 の3点での最悪値を最良とすることを考えよう。
乗数2の場合、σ max が0.8 付近がほぼ最良で、それよりもσ maxを大きくした場合 P3での値は改善してもP2, P1での値が悪化している。乗数が3の場合、グラフからσ max が 1.4~1.6 あたりが最良で、その時の反射は 1.0E-5 と推測される。
乗数4の場合、σ max 2.0 より大きいところに最良点がありそうに見える。では、σ maxは どこまで大きくすれば良いか? 式2に従えば、absorption coefficients が2.0を超えると発振してしまう。が、式4を使っている場合、音圧および粒子速度計算点のσが 2.0を超えなければ問題ないはずである。そこで、計算に使用するσの最大値を横軸にとって反射量を図にしたものが、fig 5-5である。図から、乗数が4の場合 σ max に 2.1 にすることが最良と読み取れる。では、乗数をさらに増やすとどうか。乗数が5の場合、P3地点 (浅い入射角)での値を十分下げきれない。Fig 5-3 と合わせてみるに、乗数が4が最良と読み取れる。

Fig. 5-5
結果
PML (Perfectly matched layer) を具体的に構成するために、absorption coefficients のσ max と 乗数M の最適値を計算実験で探った。
M とσ max は、相互に関係しておりセットで最適値を探索する必要があることを見出した。
単精度の計算でPMLが16層である場合、乗数M=4、σ max = 2.1 が最適で、剛な境界の場合に対して反射を 1.7 E-6 程度に減衰させることができることを見出した。
[1] Ludovic Métivier, Laurence Halpern. Perfectly Matched Layers equations for 3D acoustic wave propagation in heterogeneous media. WAVES 2011, Jul 2011, Vancouver, Canada. ⟨hal-00826617⟩
[2] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p12-14
[3] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p9-10
[4] 宇野 亨編著 何 一偉, 有馬 卓司 共著、数値電磁界解析のためのFDTD法 -基礎と実践-、コロナ社(2016)
PMLの性能は、反射波の大きさを剛な境界の場合と比較することで評価する。単純に受音点で音圧を観測した場合、反射が小さい場合に直接波が尾を引く残余と反射波との区別が難しくなることが予想される。そこで、測定時間内には反射波が戻ってこないほど境界の位置を遠のけた場合の測定値を基準として、それとの差を反射波として抽出する。
斜めに音波が入射する場合の性能を評価するため、点音源を用い受音点を3か所設けた。剛な境界の場合、境界に対して音波が垂直に入射し反射して到達する点 P1、およそ45度で入射して反射が到達する点 P2、およそ30度で入射して反射が到達する点 P3 の3点である。音波はいったんPML層の内部に入って反射してくる。PML層が厚くなると厳密には反射角度が異なってくると想定されるが、ここでは無視できるものとして扱う。
具体的には、X 999 cm, Y 599 cm, Z 799 cm の天井以外は剛な境界で囲まれた空間に、下図のように音源と受音点を配置した。Spacial stepは1cm、 time step は 0.01ms。音速cは330m/s、空気密度は1.2047291 kg/m3を使用。CFLは0.33 である。

Fig 3-1 配置図
反射波の大きさには、音圧の絶対値の最大値を使用する。より具体的には、P1では計算開始から11.50msから14.50msまでの3.0ms、P2では16.60msから19.60ms、P3では23.90msから26.90ms の音圧の絶対値の最大値を用いた。
音源は、音源となるセルの音圧を1kHzのsin波で1周期分だけ強制的に与えるという簡便な方法を採用した。
計算は単精度で行った。
4. PMLの層数と反射量
PMLの層数のみを変更し、反射量の関係を調べる。
PMLの層数を8から256まで変え、その他は次の条件で一定とした。Absorption coefficients σには式5を採用し、乗数Mを2, σMAX は 1.0 。音源は、1kHzのsin波1周期。
計算した各受音点での反射波の絶対値のピークを剛な境界の場合を1として現したものが次の図である。

Fig 4-1 PML層数と減衰
Fig.4-1 で示すようにPML層数を指数関数的に増加させることで反射波は指数関数的に減少する。100層あたりで反射波の減少が底を打つが、これはPML層に入射しつつある音圧に対して、単精度浮動小数点の有効桁数(十進で6桁強)では不足するほど反射波の音圧が小さくなりすぎたことにより発生するノイズが卓越するためと考える。
Fig.4-1で興味深い点は、PMLが10層以下であるとPMLへ浅い角度で入射する音波の減衰が特に悪いが、層数を増やすことで顕著に改善される点である。
具体例として、受音点P2における16.6msから19.6msまでの反射波の音圧波形を示す。波形を見やすくするため、音圧のスケールはすべて異なる。青線でしめす剛な境界からの反射波形と比べると、PMLが8層の場合の反射波形はおおむね元の形状をとどめているが、PMLが64層になると反射波形はノイズまみれとなっている。

Fig. 4-2 受音点 P2 での反射波の波形
5. Absorption coefficientsと反射量の関係
Absorption coefficients σに式5を採用した場合、乗数Mとσ max の二つのパラメータとPMLでの反射量の関係を検討する。
fig.5-1は、σmaxを1.0に固定し乗数を1から4まで変えた時の反射量を示す。PMLの層数は16で固定である。

Fig. 5-1
入射角が直角(P1)の場合は乗数が増えるほど反射量が減るが、角度が浅くなるほど反射量が最低となる乗数があることが見える。σ maxが1.0の場合、角度によらない結果を求めた場合では乗数として2が最適で、その場合の反射は1.0E-4以下 (吸収率99.99% 以上) と読み取れる。さらに、σ maxを変えて変えてみる。実は、Absorption coefficents は1.0を超えても吸収層として働く。

Fig. 5-2

Fig. 5-3
fig. 5-2, fig. 5-3は、σ maxを1.2にした場合とσ maxを2.0にした場合の図である。
σ maxを大きくするほど入射角が浅いケースでの反射量が最低となる乗数が増えるとともに、反射量の最低値も減少することが見て取れる。
Fig 5-4は、σ max によって減衰量がどのように変化するかと異なる乗数ごとに追った図である。

Fig. 5-4
角度に因らない結果を求めP1, P2, P3 の3点での最悪値を最良とすることを考えよう。
乗数2の場合、σ max が0.8 付近がほぼ最良で、それよりもσ maxを大きくした場合 P3での値は改善してもP2, P1での値が悪化している。乗数が3の場合、グラフからσ max が 1.4~1.6 あたりが最良で、その時の反射は 1.0E-5 と推測される。
乗数4の場合、σ max 2.0 より大きいところに最良点がありそうに見える。では、σ maxは どこまで大きくすれば良いか? 式2に従えば、absorption coefficients が2.0を超えると発振してしまう。が、式4を使っている場合、音圧および粒子速度計算点のσが 2.0を超えなければ問題ないはずである。そこで、計算に使用するσの最大値を横軸にとって反射量を図にしたものが、fig 5-5である。図から、乗数が4の場合 σ max に 2.1 にすることが最良と読み取れる。では、乗数をさらに増やすとどうか。乗数が5の場合、P3地点 (浅い入射角)での値を十分下げきれない。Fig 5-3 と合わせてみるに、乗数が4が最良と読み取れる。

Fig. 5-5
結果
PML (Perfectly matched layer) を具体的に構成するために、absorption coefficients のσ max と 乗数M の最適値を計算実験で探った。
M とσ max は、相互に関係しておりセットで最適値を探索する必要があることを見出した。
単精度の計算でPMLが16層である場合、乗数M=4、σ max = 2.1 が最適で、剛な境界の場合に対して反射を 1.7 E-6 程度に減衰させることができることを見出した。
[1] Ludovic Métivier, Laurence Halpern. Perfectly Matched Layers equations for 3D acoustic wave propagation in heterogeneous media. WAVES 2011, Jul 2011, Vancouver, Canada. ⟨hal-00826617⟩
[2] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p12-14
[3] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p9-10
[4] 宇野 亨編著 何 一偉, 有馬 卓司 共著、数値電磁界解析のためのFDTD法 -基礎と実践-、コロナ社(2016)










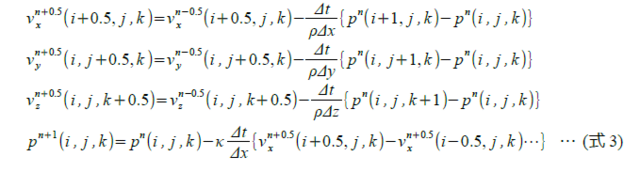 …式3
…式3 …式4
…式4
 …式5
…式5







