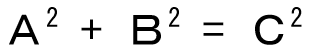いよいよ終わりに
今回でいよいよ計算法シリーズもこれで終わりにします。ダラダラと思いついたまま書いていると駄文が増えるばかりですので・・・。が、最後にシメとしてひと言。
暗算のテクニック
必ずどれか一つだけでも覚えて、家族や友達を驚かせてください。知識はというものは他人に教えることで必ず身につきます。
それと暗算の極意というべきものも覚えておいてください。
これまでは掛け算の暗算法の紹介でしたが、加算・減算でも暗算は使うべきです。計算の早い方、頭の良い方は必ずこの方法を利用しています。
極意 その1
加減算する場合、両方の数値または一方の数値を、キリのよい数値に必ず丸めて(置換して)計算すること。計算がとてもラクに早くなります。
・ キリの良い数字だと瞬時に計算できます。
・ 桁数が少ない程、計算速度が上がります。
例題
① 123+456 ⇒ 100+23+456=556+23=559 579
② 3724+891 ⇒ 3700+24+900-9=4600+(24-9)=4600+15=4615
③ 234-56=234-(60-4)=174+4=178 または
=230ー60+(4+4)=170+8=178 と考えます。
極意 その2
基本的に掛け算でも足し算でも上位から(左から右へ)計算すること。
(但し、×11のように隣同士を足して繰り上げの多いときは、右から答えを書く必要のある場合もありますが、殆ど一瞬で判断できます。)
23 56 従来法(右から左へ)で計算するとき
+)45 ×) 78 繰り上がり数字を覚えるのも、直前の
→ → 計算値を覚えるのも変りません。
極意 その3
やさしい因数分解の公式に当てはめて計算
多くの数字は、(a+b)、(a-b)、(a-c)のような組み合わせです。
今回でいよいよ計算法シリーズもこれで終わりにします。ダラダラと思いついたまま書いていると駄文が増えるばかりですので・・・。が、最後にシメとしてひと言。
暗算のテクニック
必ずどれか一つだけでも覚えて、家族や友達を驚かせてください。知識はというものは他人に教えることで必ず身につきます。
それと暗算の極意というべきものも覚えておいてください。
これまでは掛け算の暗算法の紹介でしたが、加算・減算でも暗算は使うべきです。計算の早い方、頭の良い方は必ずこの方法を利用しています。
極意 その1
加減算する場合、両方の数値または一方の数値を、キリのよい数値に必ず丸めて(置換して)計算すること。計算がとてもラクに早くなります。
・ キリの良い数字だと瞬時に計算できます。
・ 桁数が少ない程、計算速度が上がります。
例題
① 123+456 ⇒ 100+23+456=556+23=
② 3724+891 ⇒ 3700+24+900-9=4600+(24-9)=4600+15=4615
③ 234-56=234-(60-4)=174+4=178 または
=230ー60+(4+4)=170+8=178 と考えます。
極意 その2
基本的に掛け算でも足し算でも上位から(左から右へ)計算すること。
(但し、×11のように隣同士を足して繰り上げの多いときは、右から答えを書く必要のある場合もありますが、殆ど一瞬で判断できます。)
23 56 従来法(右から左へ)で計算するとき
+)45 ×) 78 繰り上がり数字を覚えるのも、直前の
→ → 計算値を覚えるのも変りません。
極意 その3
やさしい因数分解の公式に当てはめて計算
多くの数字は、(a+b)、(a-b)、(a-c)のような組み合わせです。
そのような場合の二乗計算や掛け算に使える公式は比較的簡単なものです。
極意 その4
できるだけ沢山練習をして、数字の特徴を瞬時に見つけることです。
まとめ(1~10)
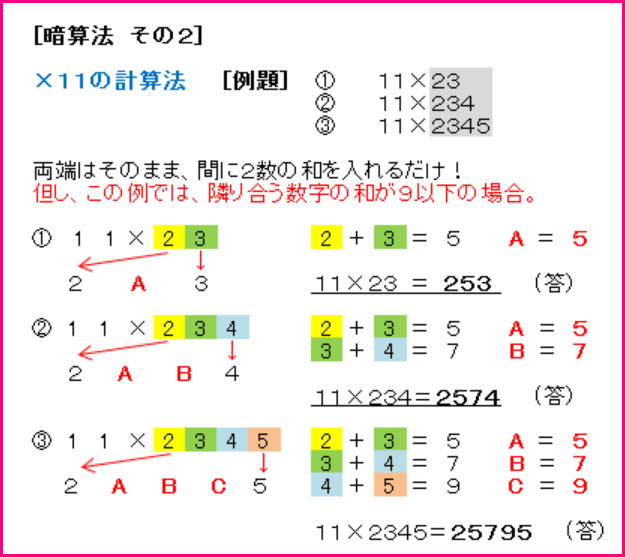
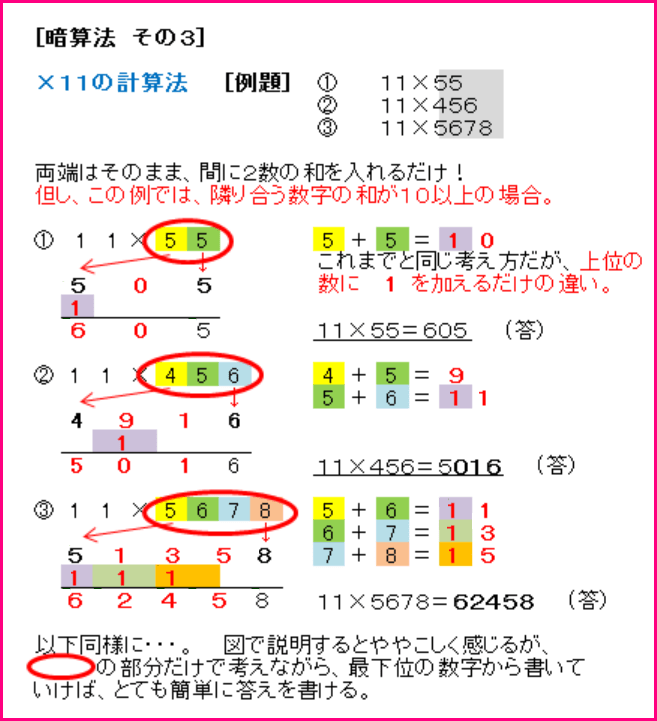
1)×11の暗算
両端そのまま、隣同士を足して書く(10を超えた場合は上位に+1)
極意 その4
できるだけ沢山練習をして、数字の特徴を瞬時に見つけることです。
まとめ(1~10)
1)×11の暗算
両端そのまま、隣同士を足して書く(10を超えた場合は上位に+1)
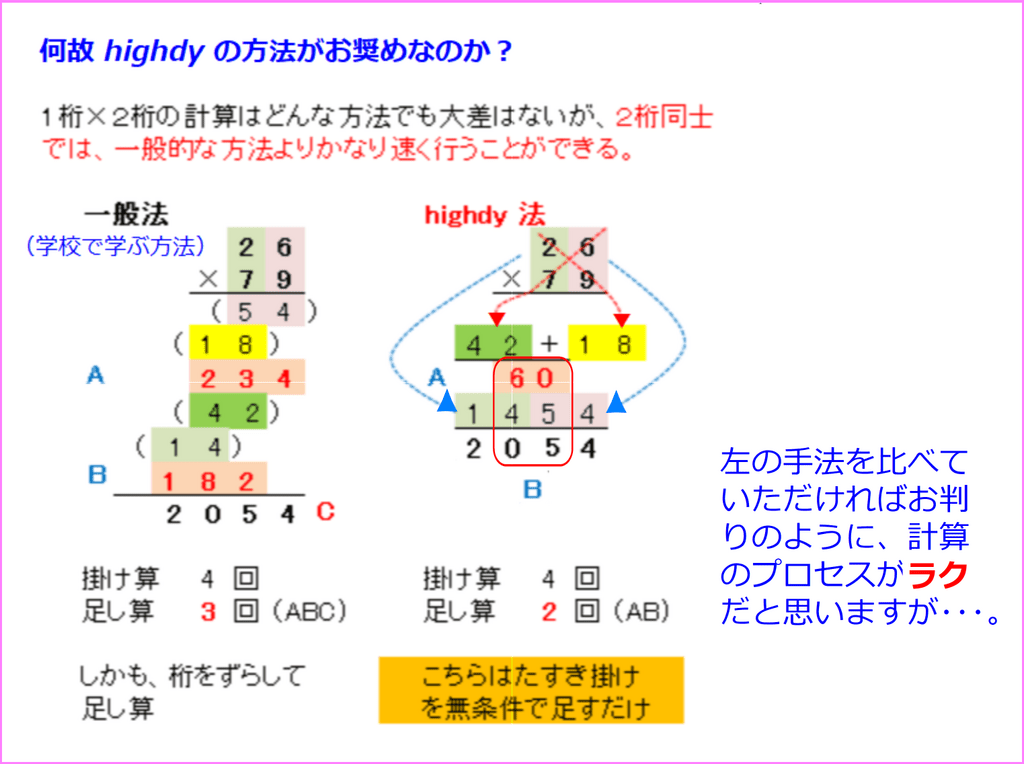
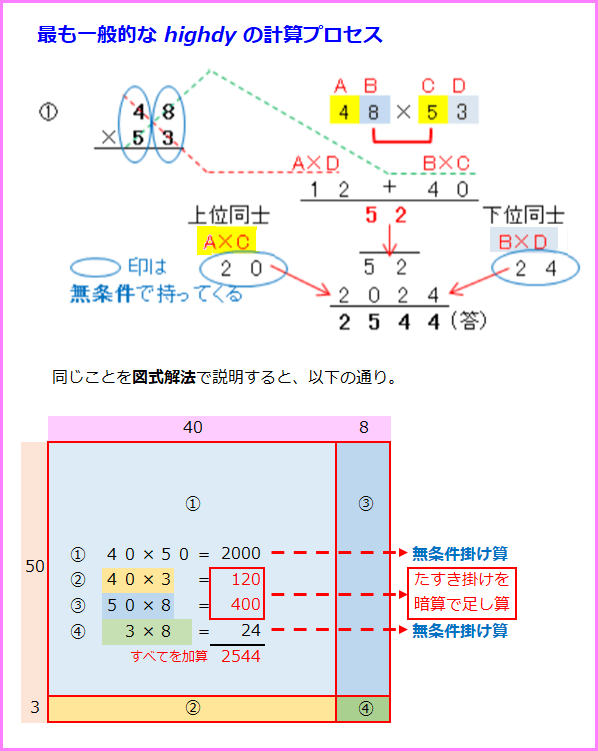
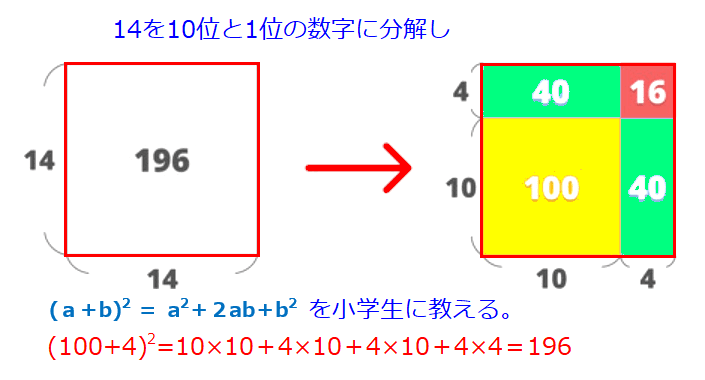
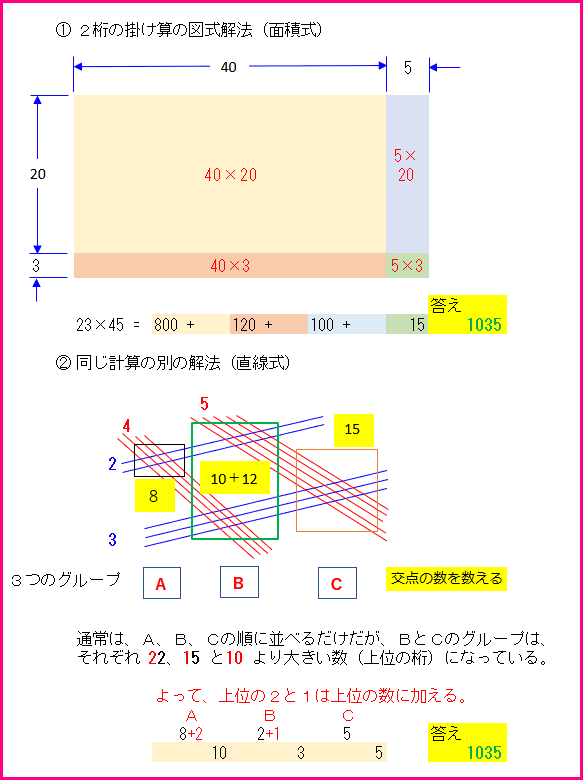
2)2桁同士の掛け算では図式解法を思い出す。面積式・直線式
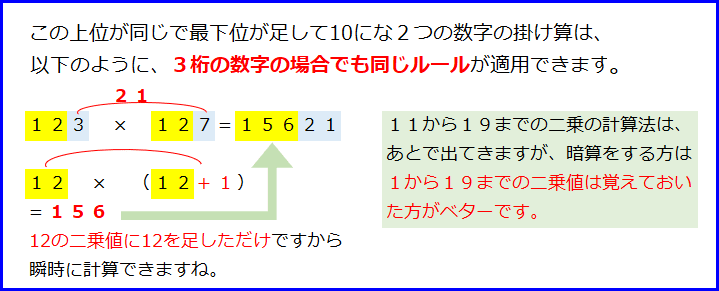
3)2桁同士の掛け算で10位が同じで1位が足して10
10位の一方に+1をして掛け算、その右隣に1位同士の掛け算を並べるだけ。
10位の一方に+1をして掛け算、その右隣に1位同士の掛け算を並べるだけ。
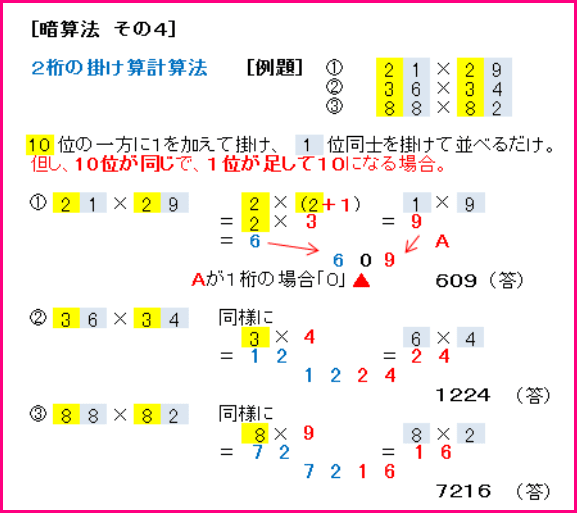
4)2桁同士の掛け算で1位が同じで10位が足して10
10位同士の掛け算に1位の数字を加えて書き、その右隣に1位同士の掛け算を並べるだけ。
(但し、落とし穴に注意、1位の掛け算が1桁だったときは、左に0をつける。)
メチャ簡単な掛け算(二乗)計算例
10位同士の掛け算に1位の数字を加えて書き、その右隣に1位同士の掛け算を並べるだけ。
(但し、落とし穴に注意、1位の掛け算が1桁だったときは、左に0をつける。)
メチャ簡単な掛け算(二乗)計算例
25×25、35×35、45×45、・・・・・・これほど簡単な計算はない!
2×(2+1)の隣に25 625、3×(3+1)の隣に25 1225、・・・・・・
2×(2+1)の隣に25 625、3×(3+1)の隣に25 1225、・・・・・・
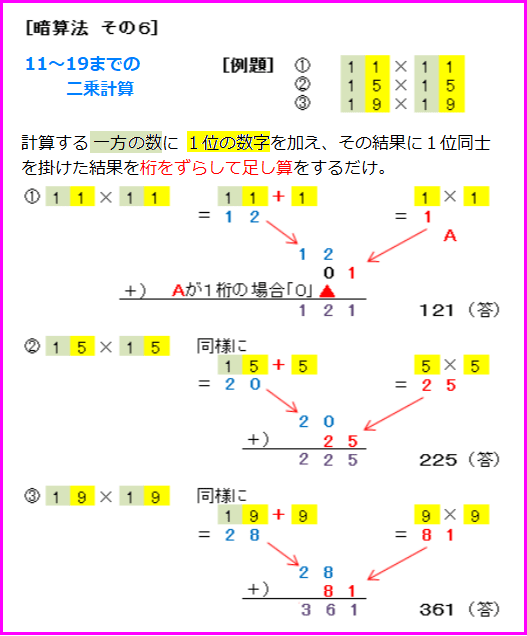
5)11~19までの二乗計算
4)によく似ているので注意! 計算する一方の数字に1位の数字を加え、その右隣りに位同士の掛け算を1桁上位方向にずらして足し算するだけ。
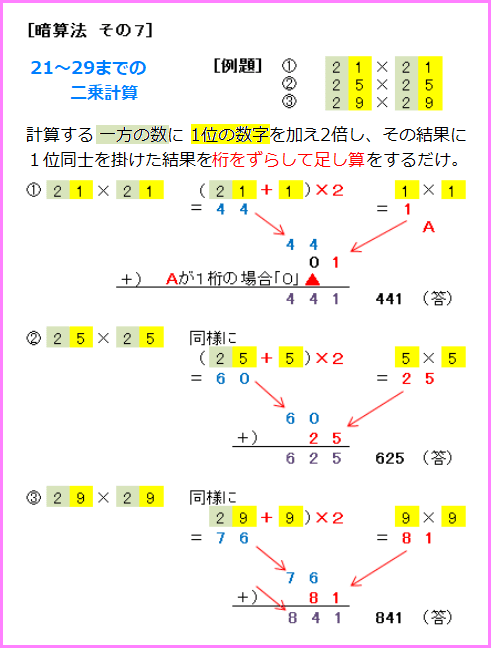
21~29までの二乗計算
上記に似ているが、計算する一方の数字に1位の数字を加え後に2倍が必要、以下同じ。但し30台以上では実用性が低く、30台以上の二乗計算では、以下の公式を使った方が速いこともある。
(人によっては、公式に頼らなくても暗算が速かったり、30位までなら覚えておられる方も多い。)
4)によく似ているので注意! 計算する一方の数字に1位の数字を加え、その右隣りに位同士の掛け算を1桁上位方向にずらして足し算するだけ。
21~29までの二乗計算
上記に似ているが、計算する一方の数字に1位の数字を加え後に2倍が必要、以下同じ。但し30台以上では実用性が低く、30台以上の二乗計算では、以下の公式を使った方が速いこともある。
(人によっては、公式に頼らなくても暗算が速かったり、30位までなら覚えておられる方も多い。)

6)因数分解の公式で置換し暗算をラクにする
例題 ① 32×37、② 24×16、③ 21×19

2×5(=10)、4×5(=20)などに分解できる掛け算は、優しい計算に置換する。
15×18=3×5×2×9と同じなので、27×10=270 と簡単になる。
12×35=3×4×5×7と置換しても良いので、21×20=420 と計算できる。
7)highdy 式の「最も一般的な計算プロセス」
これまで方法のどれも思い浮かばない人は。この方法による。
両側そのまま、たすき掛けあんこを加える方法。2桁でも3桁でもできるが掛け算で繰り上げ数が出た場合は上位に加えることを忘れないこと。
これまで方法のどれも思い浮かばない人は。この方法による。
両側そのまま、たすき掛けあんこを加える方法。2桁でも3桁でもできるが掛け算で繰り上げ数が出た場合は上位に加えることを忘れないこと。
8)highdy 式は3桁でも考え方は同じ。
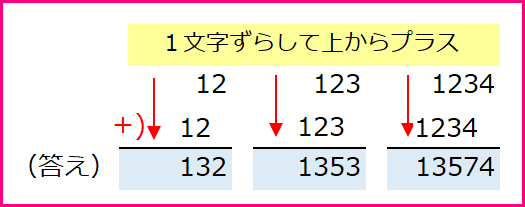
9)2秒で答えが書ける×11の計算
2桁なら2秒で答えが書ける程簡単で、何桁になっても方法は同じ。
でもできることなら、繰り上げを予想しながら、上位(左)から答えを書く習慣にした方がよい。
上位が同じ数字なら、インド式が速いことも。
9)2秒で答えが書ける×11の計算
2桁なら2秒で答えが書ける程簡単で、何桁になっても方法は同じ。
でもできることなら、繰り上げを予想しながら、上位(左)から答えを書く習慣にした方がよい。
上位が同じ数字なら、インド式が速いことも。
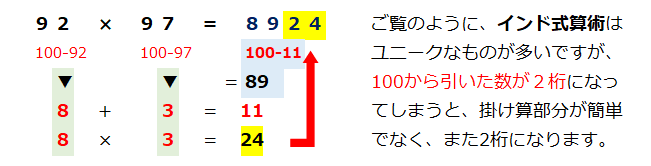
10)インド式算術の置換(変換)法
掛け算や割り算では、その順番を入れ替えても結果は同じであるので、先に学んだ置換法による計算をラクにする方法を考える。
インド式では5や25を10÷2や100÷4として利用し、計算の簡略化を図っている。
すべての計算は、極意にもある通りキリの良い数字に置き換えることで、計算がラクになる。
11)ゴースト暗算とインド式計算
少し余裕のある方は、highdy 法とは異なる手法を研究してみるとよいと思います。
いずれの場合も、沢山練習して、瞬時に適切な計算法が思い出せるようでないと、どの方式も実用的には使えませんが、どれか一つ覚えておいても損はしない知識だと思います。
本日もご来訪いただきありがとうございました。