0と1の間の無限

カントール集合

カントール集合は、フラクタルの1種で、閉区間 [0, 1] に属する実数のうち、その三進展開のどの桁にも 1 が含まれないような表示ができるもの全体からなる集合である。1874年にイギリスの数学者ヘンリー・ジョン・スティーヴン・スミス（英語版）により発見され1883年にゲオルク・カントールによって紹介された。

　カントールの三進集合とも呼ばれフラクタル概念の生みの親であるブノワ・マンデルブロは、位相次元が 0 の図形をダスト（塵）と呼び、カントール集合のことはカントール・ダストやカントールのフラクタルダストと呼んでいた。(wiki)

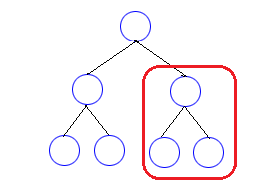
これをもっとわかりやすく視覚化したのがツリー構造です。

複雑に枝分かれするパターン

　数学的な表現はチンプンカンプンですが、要するに直線の中央の線分の1/3を削除し、残った部分の中央の1/3をまた削除する。そしてこの作業を永遠に続ける。すると最後にはほぼ空白ながら、限りなく短い直線が限りなく多く残るということです。

0と1の閉ざされた有限の中に無限が入り込んだのです。

カントール集合最終のイメージ。

コッホ雪片

　1905年、スウェーデンの数学者コッホはカントールの手法を応用して、のちにコッホ曲線と呼ばれる自己相似な図形を考案しました。コッホ曲線はコッホ雪片の一部として紹介されることが多い。コッホ雪片はひとつの三角形から始まり、各辺の中央の1/3を三角形に置き換えるという作業を際限なく繰り返す。その結果、辺が無限に長く、面積が有限という初期の幾何学者を困惑させるような図形ができる。

(創元社　深遠なる「幾何学の世界」より)

辺の長さは無限で面積は有限です。

0と1という有限の中に無限があるというのは矛盾です。また無限の長さの線分に囲まれた有限な図形も矛盾です。ところがこの矛盾の場所というのが「スーパーポジション」すなわち「共存の場所」なのです。

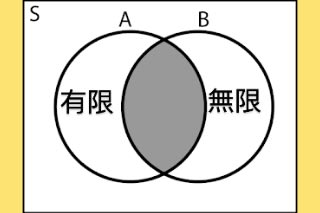
「有限であり、かつ、

無限」ということです。

見出し画

フィラエ島にある古代エジプトの建物の柱頭にはカントール集合に似た模様が付けられている。

木構造／ツリー構造

上図の「半分にする」という分け方がよくわからないので調べたところIT用語の「木構造」に似ていることがわかりました。

木構造 【tree structure】 ツリー構造

木構造とは、データ構造の一つで、一つの要素（ノード）が複数の子要素を持ち、子要素が複数の孫要素を持ち、という具合に階層が深くなるほど枝分かれしていく構造のこと。木が幹から枝、枝から葉に分岐していく様子になぞらえた名称である。

　　　　　　　(IT用語辞典より)

　現実の木は地中の根から上に向かって幹や枝を伸ばし、葉が上方にあるが、木構造を図示する際にはこれとは逆に、根ノードを図の最上部に描き、一段下に子ノード群、その下に孫ノード群、といった具合に下向きに広がるように描くことが多い。家系図の描き方と同じである。

２分木(Binary Tree)

　下の図のような形のデータ構造を２分木という。それぞれの節(○)は、最大2つの枝を持ち、その枝先には、さらに節を持つ。枝を持たない節を葉ともいう。データの整列や探索などに使用される。

再帰的な性質

上図は、二分木の概念図に、赤い枠を加えたものです。

二分木の一部分を囲っていますが、この囲まれた部分だけを観察してみると、その部分もやはり二分木になっていることが分かります。

　このように、木構造はその一部分だけを取り出してみても、やはり木構造の形をしているという特徴があります。ここで、一部分の木のことを部分木と呼びます。

　この概念図の場合、全体としての根の右側にある部分木を囲っていますが、この場合、根に対して右部分木と呼びます。左側にあれば左部分木と呼ばれます。

　もっと大きな木構造であれば、部分木の中にさらに部分木が、その中にさらに部分木があるという構造になります。このように、自分自身の一部が、自分自身と同じ形状をしているような構造は、再帰的な構造と呼ばれます。

二分木 | Programming Place Plus　アルゴリズムとデータ構造編【データ構造】　第７章より

　図形の「フラクタル構造」の説明と情報の「ツリー構造」の説明を比べて読むと、両者が驚くほど似ているのに気がつきます。あるいは同じことをそれぞれの分野での言葉で言っているだけかもしれません。

見出し画　セェフィロトの樹

生命の樹（せいめいのき、英語: Tree of Life）は、旧約聖書の創世記（2章9節以降）にエデンの園の中央に植えられた木。命の木とも訳される。生命の樹の実を食べると、神に等しき永遠の命を得るとされる。

ユダヤ教のカバラではセフィロトの木（英語: Sephirothic tree）とも呼ばれ、宇宙万物を解析する為の象徴図表に位置付けられている。(wiki)