前回に引き続き2次体の整数を用いてn乗数の和で2通りに表される自然数の例を考える。今回はn=6の場合。
本来のタクシー数は、2通りの立方数の和としてあらわされる自然数のことであった。この時、立方数の一方が6乗数であれば、その数は2通りの2次体整数の6乗数の和としてあらわされる。例えば、

の場合、1の3乗と9の3乗は6乗数のため
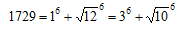
と2次体の整数の6乗の和として表わされる。
以下、2次体の整数の6乗数の和として表わされる場合をもう少し一般的な形で考えてみる。

よって α=a β=√m とおくと

したがって、
 ……………… (1)
……………… (1)
とおくと
 ……………… (2)
……………… (2)
(1) でx+y=s, xy=t とおくと

この右辺を とおくと
とおくと

 のときx,yは、
のときx,yは、 の解である。これを解くと
の解である。これを解くと

 のときx,yは、
のときx,yは、 の解である。これを解くと
の解である。これを解くと

よって、(2)より

両辺を2の6乗で割れば

したがって、2次体整数の6乗数の和として、2通りに表せる組を見つけるには、以下の手順で行えばよい。
①  が等しくなる組(s,t)を求める。
が等しくなる組(s,t)を求める。
② 2次方程式を解いて、(s,t) から (x,y) を求める。
③ x,yが2次体整数の平方であらわされるかどうか確かめる。
④ ③が成り立てば(2)より6乗数の和として2とおりに表せる。









