楕円曲線といえばWeierstrassの標準形の

もしくは

の形で通常扱われるが、4次の楕円曲線もあるようだ。
タクシー数(その7)で4次の楕円曲線

が出てきたので、3次と4次の楕円曲線はどのような関係にあるのか少し調べてみた。
結論から言うと、有理点を有する4次楕円曲線は、双有理変換でWeierstrass標準形に変換できる。
例えば、インターネットで見られる”Elliptic Curve Handbook, Ian Connell, February,1999”
のP105に出ている。これを追ってみると、
有理点(μ, ν)=(p,q)を持つ4次楕円曲線はμをμ+pに置き換えて

としてよい。このとき、Weierstrass標準形への変換は、

ここで、 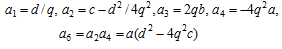
とするとき、、Weierstrass標準形を満たす。
逆変換は


で与えられる。
このとき、 は,
は,  に変換される。
に変換される。
これをタクシー数(その7)で出てきた4次楕円曲線に適用すると以下のとおりである。

ひとつずつ追ってみると
➀ 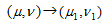
もともとの4次楕円曲線は有理点(1,36)を持つので、x座標が0となるようにした。
② 
上記のWeierstrass標準形への変換
 に注意すればよい。
に注意すればよい。
③ 
xの2乗の係数が0となるWeierstrassの標準形への変換
である。
 の変換で、有理点(1,36)→無限遠点 、(-35,29052)→(2920,145376)となる。
の変換で、有理点(1,36)→無限遠点 、(-35,29052)→(2920,145376)となる。
Weierstrassの標準形の楕円曲線の場合は、オープンソースの数式処理システムsageにより、
簡単に有理点が求められる。Sageの処理結果によると、3次曲線の有理点のなする群は
ZxZxZ/2Z であり、P1,P2をZxZの、TをZ/2Zの生成元とすると
P1=(-308, 9568), P2=(1720,52624), T=(-216,0)
である。Sageで絶対値の小さなl,m,nについて、3次曲線の有理点を求め、上の変換式を用いて
4次曲線の有理点に変換し、そこからタクシー数(その7)の方法で6乗数と3乗数の和で2通りに
表せる数を求めてみた。その結果は下表のとおりである。




すべて6乗数と3乗数がすべて自然数の組み合わせは3つのみであった(黄色で網掛け)。
なかなか、そのような組み合わせを作るのは難しいかもしれない。なお、これらの
数値の計算には、CoCalc (SageMathCloud) http://www.sagemath.org/ を用いた。









