メモ8で 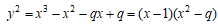 q≠0,1の非負整数
q≠0,1の非負整数
の位数∞の整数解について考えた。その時、整数解の数が少ないことと、2倍すると整数でなくなることが多いと感じていたが、一般的にはまったくそのようなことはなく、自然数nを与えた時、n以下の自然数kについて整数解のk倍がすべて整数解となる有理数体上の楕円曲線が存在する。考えてみればあたりまえのことであるが、忘れないようにメモしておく。
(命題) 自然数nを与えた時、n以下の自然数kについて整数解のk倍がすべて整数解となるQ上の楕円曲線が存在する。
(証明)楕円曲線  上の点
上の点 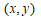 について、
について、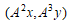 は、
は、
楕円曲線  上の点である。
上の点である。
なぜなら、 の両辺にAの6乗をかけると
の両辺にAの6乗をかけると
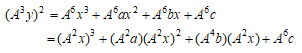
となることより明らかである。
ここで 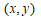 を楕円曲線
を楕円曲線  (a,b,cは整数)の整数点とし、n以下の自然数kについて、k*Pを求め、そのx座標の分母の最小公倍数について素因数分解したときの各素因子の指数が偶数のときは1/2、奇数のときは(指数+1)の1/2とした自然数をAとする。この時、k*Pのx座標にAの2乗をかけると、Aの作り方より、整数となる。y座標にAの3乗をかけた数も上に述べたことより整数となる。 (証明おわり)
(a,b,cは整数)の整数点とし、n以下の自然数kについて、k*Pを求め、そのx座標の分母の最小公倍数について素因数分解したときの各素因子の指数が偶数のときは1/2、奇数のときは(指数+1)の1/2とした自然数をAとする。この時、k*Pのx座標にAの2乗をかけると、Aの作り方より、整数となる。y座標にAの3乗をかけた数も上に述べたことより整数となる。 (証明おわり)
具体的な例についてみてみよう。
楕円曲線  を考える。
を考える。
Cocalcで有理点を求めると 生成元が (-1,17)と(0,24)、ねじれ元が(-2,0) である。
P=(0,24) とすると
2P =(34 ,-228 )
3P=(5472/289,571560/4913)
4P=(37009/12996,-56131883/1481544)
5P=(2215366560/4739329,104563839488088/10317519233)
6P=(-263062196894/163907571025,710981873309736396/66358799667326375)
である。ここで5倍まで整数点とすることを考える。
2Pのx座標の分母= 1
3Pのx座標の分母= 
4Pのx座標の分母= 
5Pのx座標の分母= 
なので
A=
とする。この時楕円曲線の方程式は もとの方程式が  であることより
であることより

であり、 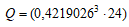 とすると、
とすると、
Q=(0, 1802386172748339589824)
2Q=(605206133214984,-17122668641109226103328)
3Q=(337033173310848, 8736785406880054413120)
4Q=(50689971991729, -2845323577113009195707)
5Q=(8320571202176640, 761101959228782272595136)
6Q=(-16202610927870599861496/567154225, 10867968464008588070428992637629792/13506777868375)
となり、Q, 2Q,3Q,4Q,5Q が整数点となる。
ここではn=5としたが、nを任意の自然数として、n個以上の整数点を有する楕円曲線を同様に構成できる。









