著者：ニール・ドグラース・タイソン
マイケル・A・ストラウス
リチャード・ゴッド
訳者：松浦俊輔
発行：青土社 2018 原作：WELCOME TO UNIVERSE 2016
「第1部 恒星、惑星、生命」、「第2部 銀河」、「第3部 アインシュタインと宇宙」と地球に近いところから宇宙論までのさまざまな話題をやさしい語り口で理論的に説明している。第1部の「星はどのようにエネルギーを放射するか」の説明で黒体放射について分かったような気がした。物体は温度に応じて電磁波を放出しているということ。人間も熱を出しているからな。体温がものすごく高温になれば、そんなことはないけれども、サイヤ人みたいに光り出すというわけか。第3部の一般相対性理論、ブラックホールやインフレーションの話はよくわからなかったが、十分楽しめた本でした。
「湖底の城 9巻」
著者：宮城谷昌光
発行：講談社 2018年
P7-8 に計然と范蠡の問答の話が出てくる
「国を治める基本の方法はなんであろうか」と計然は問い、
「国民の衣食を不足させぬこと、国家の倉廩を満たすこと、このふたつでしょうか」と范蠡は答える。
これに対し、
「それは目標であって、基本ではない。百里先あるいは千里先にある物を獲るためには、歩くのか、馬車に乗るのか、船に乗るのか、それらが基本の方法である」と計然は応じ、さらに続けて、
「目的地に至るために、まず知っておかねばならぬのは、天理と地理だ。大雨になることを予測せずに、船を用意しないででかけるのは、無謀というものだ。川が涸れ、馬が斃れるほどの大旱であれば、歩くしかない。その歳がどのような天候になりやすいか、あらかじめ知っている者と知らない者との差は大きい。地理についても、同様の予備知識が要る。目的地への大小の道を丁寧に調べ、地図を作っておく。近道がかならずしも近道にならず、迂路がかならずしも迂路にならぬことくらい、たれにもわかっているが、間道をふくめたさまざまな道をあらかじめ調べておく者は寡ない」と語る。
地図の必要性について簡潔に述べている。
計然の話は、史記の貨殖列伝 第六十九 に出てくる。但しそこでは表題のとおり経済的な話で国を治める話ではない。とすると、湖底の城の話は作家の創作か。
q≠0,1の非負整数
の位数∞の整数解について考える。結果を先に記すと以下のとおりである。
(命題) 楕円曲線E： q≠0,1の非負整数 の位数∞の整数解はqが以下のときに限り存在する。
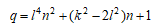l,k: 自然数、n:0でない整数
このとき、
は位数∞の整数解。また、
は位数2の整数解であり、
(説明)
(x,y)が楕円曲線Eの整数点とする。
(ｌは自然数、nの素因数の指数は1) と平方数と非平方の積に分けると、
は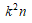 
(kは自然数)
でなければならない。したがって、
より
となる。nを-nとすれば求める式となる。この時
よって、
は、Eの整数点となる(位数∞であることは示す必要がある)。
次に PとQ= (1,0)を結ぶ直線の方程式は
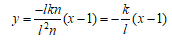
であり、この直線とEの交点のうちP,Q以外の点は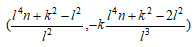 
である。
したがって、P+Qはこの座標のy座標の符号を逆転させた点である。 (説明終)
この命題より、Pが整数点のとき P+Q も整数点になるのはkがlの倍数になっている時に限る。
また、Pの整数倍は整数点にはなりそうもない。よって、異なる(l,k,n)に対しqの値が同じになれば楕円曲線Eのランクが2以上になる可能性が高い。
簡単のために以下l=1とする。この時、
である。k,nの値が小さい場合のqの値を計算してみると下表のとおりである。
|
k n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
3 |
9 |
19 |
33 |
51 |
73 |
99 |
129 |
163 |
|
3 |
7 |
16 |
31 |
52 |
79 |
112 |
151 |
196 |
247 |
|
4 |
13 |
25 |
45 |
73 |
109 |
153 |
205 |
265 |
333 |
|
5 |
21 |
36 |
61 |
96 |
141 |
196 |
261 |
336 |
421 |
|
6 |
31 |
49 |
79 |
121 |
175 |
241 |
319 |
409 |
511 |
|
7 |
43 |
64 |
99 |
148 |
211 |
288 |
379 |
484 |
603 |
|
8 |
57 |
81 |
121 |
177 |
249 |
337 |
441 |
561 |
697 |
|
9 |
73 |
100 |
145 |
208 |
289 |
388 |
505 |
640 |
793 |
(赤字は、素数)
この表より、素数ではq=73,31,79 について異なる(l,k,n)の組よりその値が得られる。そこで、上の命題より整数点を求めてみると、
● q=73：
(l,k,n) = (1,6,2) のとき P1=(-1,12) が整数点。 P1+Q=(37,216)
= (1,1,9) のとき P2=(-8, 9) が整数点。 P2+Q=(9,8)
であり、P1+P2=(499/49, -5760/343), P1-P2=(19,-72) となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
● q=31：
(l,k,n) = (1,3,3) のとき P1=(-2,9)が整数点。 P1+Q=(11，30)
= (1,1,6) のとき P2＝(-5,6)が整数点。 P2+Q＝(6，5)
であり、P1+P2=(9,-20), P1-P2=(33,-184)となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
● q=79：
(l,k,n) = (1,5,3) のとき P1=(-2,15)が整数点。 P1+Q=(27,130)
= (1,3,6) のとき P1=(-5,18)が整数点。 P2+Q=(14,39)
であり、P1+P2=(9,4),P1-P2=(129,-1456)となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
なお、83 以外のq<100の素数で楕円曲線Eの有理点群のrankが2となるのはこの３つのみである。83については、Cocalcで計算結果が出なかった。
● q=421：
(l,k,n)=(1,1,21), (1,5,12), (1,9,5), (2,7,4), (3,11,-3) が条件を満たす。
ここで 
が解ならば 
も解、 
が解ならば 
も解、なのでそのような解は除いた。他にも解があるかもしれない。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは3である。
qをうまく定め、多くの整数点を有するようにすれば、対応する楕円曲線Eのrankは大きくなる可能性があると思われる。
