タクシー数 その10 で真の意味において実2次体の5乗和で2通りに表せる例を示した。ここでは、その求め方を記しておく。
 …(A)
…(A)
の有理数解 k, δ, b について
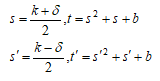
とするとき、
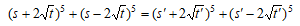
であった。ここでt、t'が有理数の2乗であれば、s≠s'のとき2通りの5乗和で表されることがわかる。なぜなら、 とすると5乗和が等しいので
とすると5乗和が等しいので 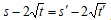 これより
これより 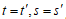 となり矛盾。
となり矛盾。 とすると
とすると 両辺を足して
両辺を足して  となり矛盾。
となり矛盾。
 とおくと
とおくと  であるので(A)は、
であるので(A)は、
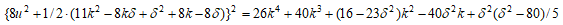
となる。左辺の中カッコ内をv、また、r=δ/kとおくと
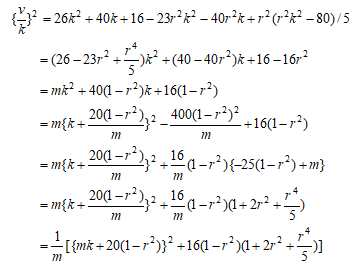
但し、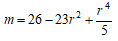
 とおくと、上の等式は
とおくと、上の等式は
 となる。この有理数解が存在するとしてその一つを
となる。この有理数解が存在するとしてその一つを  とすると、一般解は、有理数gを用いて
とすると、一般解は、有理数gを用いて
 である。よって
である。よって
 より
より
 より
より
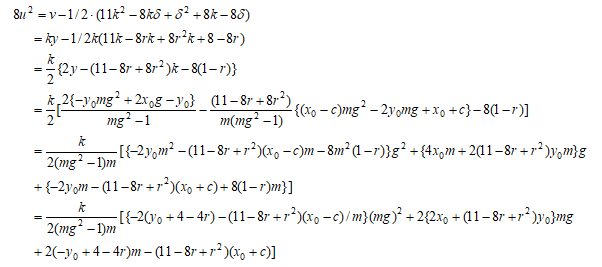
よって、T=mgとおきkをTを用いて表すと、上式は

となる。上式の左辺をYとすれば、このY,Tに関する4次式が有理点を有する、つまりT,Yに関する楕円曲線となれば、uが有理数解として求まる。
次にuとu’の関係からu'の満たすべき関係式を求める。
 より
より
 したがって、
したがって、
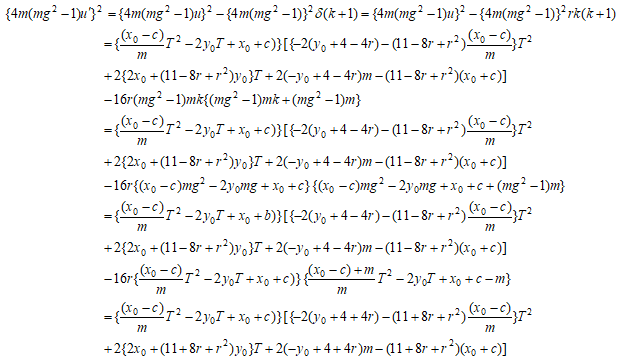
 と
と  の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。
の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。
次に、 の解を具体的に求め、u,u'が有理数となる場合を探してみる。
の解を具体的に求め、u,u'が有理数となる場合を探してみる。
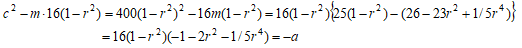
より
 が有理数の平方のとき、
が有理数の平方のとき、  は解である。
は解である。
 が平方数でない場合、r=-7/15の場合など個別の解は見つかるがパラメータ解についてはよく分からない。
が平方数でない場合、r=-7/15の場合など個別の解は見つかるがパラメータ解についてはよく分からない。
そのため、以下、  は平方数、であるとする。このとき、
は平方数、であるとする。このとき、

である。この2つの3次式の有理点で共通のT座標を有する点が見つかれば、有理数の5乗和で2通りに表される例が見つかることとなる。
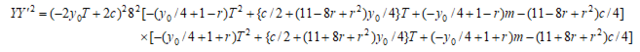
よりY, Y'に共通T座標の有理点があれば、 にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。
にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。
タクシー数 その10であげた実2次体の5乗数で2通りに表される例を求めてみる。
➀ 片方が有理数の場合
r=-3/5とする。また、 とする。
とする。
この時、Yの式は
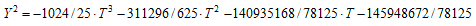
変形して
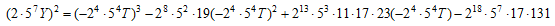
を得る。この楕円曲線の有理点の位数0の生成元をCoCalcにより求めると
(18176,523776) と (39625,442875)
を得る。前者からは、 が負となる解が得られる。したがって、実2次体の例にはならない。
が負となる解が得られる。したがって、実2次体の例にはならない。
後者から、 なる解が得られる。
なる解が得られる。
これをもとに、 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、
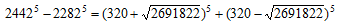
を得る。
② 双方が実2次体の例
 とする。
とする。
 の
の  の係数
の係数  が平方であれば、この4次式は有理点を有する。
が平方であれば、この4次式は有理点を有する。  とおくと、
とおくと、
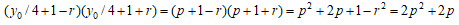
これが、有理数の平方となるためには、 つまり
つまり 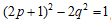 の有理数解を求めればよい。この一般解は、
の有理数解を求めればよい。この一般解は、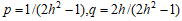 である。一方、
である。一方、 なので、
なので、
 ともパラメトライズされる。
ともパラメトライズされる。 より
より  を得る。
を得る。
よって、jを平方として  とすれば、4次式が有理点を有することになる。
とすれば、4次式が有理点を有することになる。
 とおけば、
とおけば、
 よって、
よって、

これを本ブログの「4次楕円曲線」に記した手法でWeierstrass標準形に変換して有理点を探せばよい。
今、j=4したがって、r=-15/17とすれば、楕円曲線
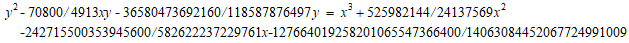
を得る。この楕円曲線の位数0の有理点をCoCalcにより求めると
(-646647040/24137569,-4628556134400/118587876497),
(-154717983680/6975757441,-2457482401059840/582622237229761),
(-525982144/24137569 , -659062103040/118587876497)
を得る。
最初の生成元より、逆変換してTの値を求め、Yの2乗を計算すると負の値になる。したがって、実2次体の例とはならない。この生成元の2倍は、
(41608541225/96550276,12315552262099515/948703011976)
となり、同様の計算をすると以下が得られる。
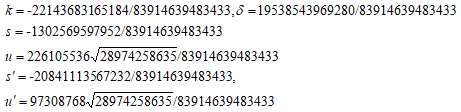
これをもとに、 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、
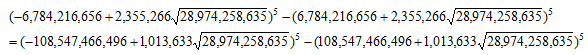
を得る。
 の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。
の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。
どなたか一緒に探しませんか。
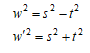 を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。 したがって、
したがって、 これが成立するのは
これが成立するのは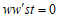 の場合に限る。
の場合に限る。 とすると、
とすると、 である。
である。 とすると
とすると となり、
となり、 である。
である。 とすると、
とすると、 となる。
となる。 とすると
とすると となり、
となり、 。したがって、必ず
。したがって、必ず となる。
となる。 について
について を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。 をかけると
をかけると よって、
よって、 より、上に述べたことより
より、上に述べたことより となる。その時、元の式に戻ると
となる。その時、元の式に戻ると である。
である。 は非平方有理数であるので、これが成り立つのは
は非平方有理数であるので、これが成り立つのは のときに限る。
のときに限る。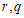 については、
については、 は
は  と非自明の例がある。
と非自明の例がある。









 …(A)
…(A)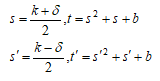
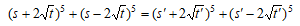
 とすると5乗和が等しいので
とすると5乗和が等しいので 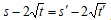 これより
これより 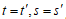 となり矛盾。
となり矛盾。 とすると
とすると 両辺を足して
両辺を足して  となり矛盾。
となり矛盾。 とおくと
とおくと  であるので(A)は、
であるので(A)は、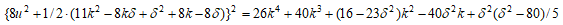
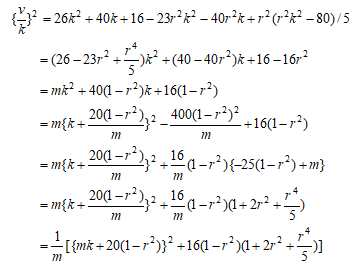
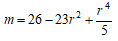
 とおくと、上の等式は
とおくと、上の等式は となる。この有理数解が存在するとしてその一つを
となる。この有理数解が存在するとしてその一つを  とすると、一般解は、有理数gを用いて
とすると、一般解は、有理数gを用いて である。よって
である。よって より
より  より
より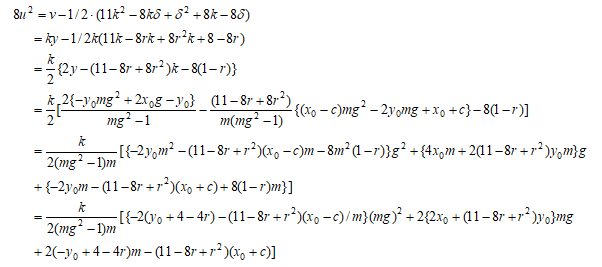

 より
より したがって、
したがって、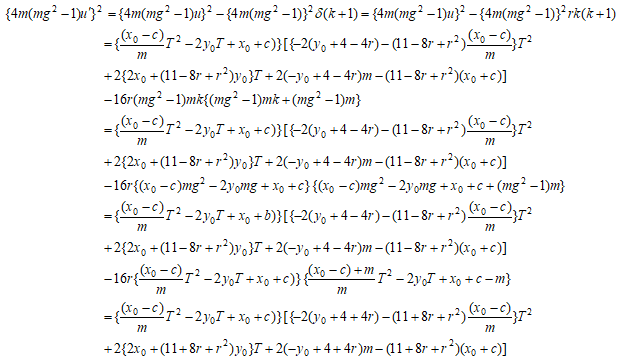
 と
と  の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。
の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。 の解を具体的に求め、u,u'が有理数となる場合を探してみる。
の解を具体的に求め、u,u'が有理数となる場合を探してみる。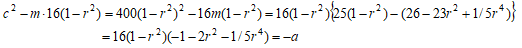
 が有理数の平方のとき、
が有理数の平方のとき、  は解である。
は解である。
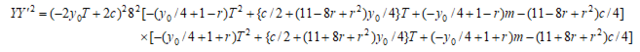
 にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。
にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。 とする。
とする。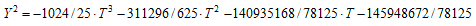
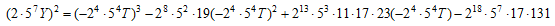
 が負となる解が得られる。したがって、実2次体の例にはならない。
が負となる解が得られる。したがって、実2次体の例にはならない。 なる解が得られる。
なる解が得られる。 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、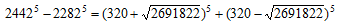
 とする。
とする。 の
の  の係数
の係数  が平方であれば、この4次式は有理点を有する。
が平方であれば、この4次式は有理点を有する。  とおくと、
とおくと、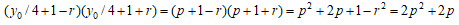
 つまり
つまり 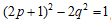 の有理数解を求めればよい。この一般解は、
の有理数解を求めればよい。この一般解は、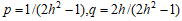 である。一方、
である。一方、 なので、
なので、 ともパラメトライズされる。
ともパラメトライズされる。 より
より  を得る。
を得る。 とすれば、4次式が有理点を有することになる。
とすれば、4次式が有理点を有することになる。 とおけば、
とおけば、 よって、
よって、
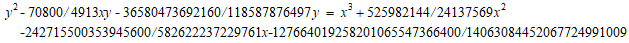
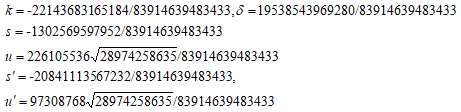
 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、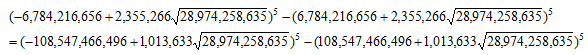
 の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。
の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。