 の有理点についてSilvermanとTateによる”Rational Points of Elliptic Curve”(1994年第2版。 以下、[Sil]と記述する。)に説明があった(p97からのExample 4)。それによると、
の有理点についてSilvermanとTateによる”Rational Points of Elliptic Curve”(1994年第2版。 以下、[Sil]と記述する。)に説明があった(p97からのExample 4)。それによると、
A. rankは2以下
B. p≡7 または 11(mod 16)のとき rank 0
C. p≡3, 5,13,15 (mode) のとき rank 1と予想されている。
D. p≡1(mod 8)のとき rank 0 または 2 と予想されている。
AとB(p≡7(mod 16))は演習問題(p105の3.8)になっている。AとBは以下のようにしてわかる。
先ず、[Sil]記載の関連事実を整理する。
①モ―デルの定理(P88):
Cを以下の方程式で与えられる整数係数3次非特異曲線とする。
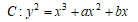
この時、C上の有理点のなす群C(Q)は有限生成アーベル群である。
②命題1 (P79):
CとC’を以下の式で与えられる整係数の楕円曲線とする。

ここで、 
T=(0,0) とし、O, O’をアーベル群C, C'の零元とするとき
(a) 以下で定義される準同型 Φ:C → C' があり、その核は{O,T}である。

(b) (a)と同じプロセスをC'に施すと、Φ’:C' → C'' があり、C''は(x,y)→(x/4,y/8)によりCと同型である。したがって、以下で定義される準同型 ψ:C' → Cがある。
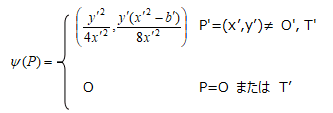
また、 は、2倍写像
は、2倍写像  である。
である。
③命題2(P85, P91):
注:命題2と[Sil]に記されているわけではない。
C, C'は命題1と同じ楕円曲線、Γ=C(Q)、Γ’=C’(Q)とおき、rをΓのランク、
α:Γ → Q*/Q*2を
α(O)=1 (mod Q*2)
α(T)=b (mod Q*2)
α(x,y)=x (mod Q*2)
とし、α’:Γ’ → Q*/Q*2も同様に定めるとき、以下が成り立つ。
αは準同型である。また、 =#α(Γ)・#α’(Γ’)/4 である。
=#α(Γ)・#α’(Γ’)/4 である。
④ランクの求め方(P93)
i.  かつy≠0 ならば
かつy≠0 ならば
 ここで、
ここで、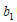 は
は の約数
の約数 
と書ける。
ii. したがって、方程式  ここで
ここで  に解(M,e,N)、M≠0がある時、楕円曲線の有理点が見つかり、
に解(M,e,N)、M≠0がある時、楕円曲線の有理点が見つかり、 はαの値域に入ることになる。
はαの値域に入ることになる。
以上の準備のもと、A.とB.を証明してみる。
今、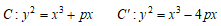 とする。
とする。
A. rankは2以下 を示す。 Cについてb=pなので、 として1,-1,p,-pが考えられる。対応する方程式は
として1,-1,p,-pが考えられる。対応する方程式は
(i) 
(ii) 
(iii) 
(iv) 
である。(ii)と(iv) にM≠0となる解はない。よって  (mod Q*2)である。
(mod Q*2)である。
C’ついて b=-4pなので、 として±1、±2、±4、±p、±2p、±4pが考えられる。上と同様の考察により。考えるべき方程式は
として±1、±2、±4、±p、±2p、±4pが考えられる。上と同様の考察により。考えるべき方程式は
(i) 
(ii) 
(iii) 
(iv) 
(v) 
(vi) 
(vii) 
(viii) 
(ix) 
(x) 
(xi) 
(xii) 
の12個である。よって、
 (mod Q*2)
(mod Q*2)
である。ここで1と4、-1と―4、pと4p、-pと-4pはmod Q*2 で等しいので、
 (mod Q*2)
(mod Q*2)
である。
よって、③より、  =#α(Γ)・#α’(Γ’)/4≦2・8 / 4 =4
=#α(Γ)・#α’(Γ’)/4≦2・8 / 4 =4
したがって、r≦2 となる。
B. p≡7 または 11(mod 16)のとき rank 0 を示す。
(i)  については (M,e,N)=(1,0,1) なる解がある。
については (M,e,N)=(1,0,1) なる解がある。
(ii) 
M偶数とするとNも偶数なので矛盾。したがって、Mは奇数。同様にNも奇数
e偶数とすると  矛盾。
矛盾。
e奇数とすると  矛盾。よって(ii)の解はない。
矛盾。よって(ii)の解はない。
(iii)  N偶数なので2N'とおく。M,eは奇数。
N偶数なので2N'とおく。M,eは奇数。
 より
より  よって p≡1または15(mod16)
よって p≡1または15(mod16)
(iv)  N偶数なので2N'とおく。M,eは奇数
N偶数なので2N'とおく。M,eは奇数
 よって、p≡1または3(mod16)
よって、p≡1または3(mod16)
(vi)  N,eは奇数 M偶数のとき
N,eは奇数 M偶数のとき
 よってp≡1(mod8) である。
よってp≡1(mod8) である。
M奇数のとき  よって、p≡5(mod8)である。
よって、p≡5(mod8)である。
(vii)  M,Nは奇数 e偶数のとき
M,Nは奇数 e偶数のとき
 よってp≡1(mod8)
よってp≡1(mod8)
e奇数のとき  よってp≡5(mod8)
よってp≡5(mod8)
(viii)  M,Nは奇数 e偶数のとき
M,Nは奇数 e偶数のとき
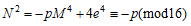 よって、p≡7(mod8)
よって、p≡7(mod8)
e奇数のとき  p≡3(mod8)
p≡3(mod8)
(ix) (iv)でM,eを入れ替えた式に相当する。よって、p≡1または3(mod16)
(x) (iii)でM,eを入れ替えた式に相当する。よって、p≡1または15(mod16)
(xi) (ii)でM,eを入れ替えた式に相当する。よって、(xi)の解はない。
以上より、p≡7 または 11(mod 16)のとき、(ii), (iii),(iv),(vi),(vii),(ix),(x)の解はない。
よって、 (mod Q*2)
(mod Q*2)
 =#α(Γ)・#α’(Γ’)/4≦2・2 / 4 =1 より r=0 となる。
=#α(Γ)・#α’(Γ’)/4≦2・2 / 4 =1 より r=0 となる。









