タクシー数 その8 で、実2次体の整数の5乗数の和で2とおりに表される例を示した。ここでは、そのような例をたくさん見つける方法を検討する。
タクシー数 その8 での議論で
 …(A)
…(A)
の有理数解 k, δ, b について

とするとき、

である。δ≠0かつ  であれば、これらが相違なる数であることがわかる。
であれば、これらが相違なる数であることがわかる。
したがって、この仮定の下でt, t'>0となる解k, δ, bを求めればよい。
なお、 のとき、
のとき、 である。
である。
(A) 式の左辺は

であるので、 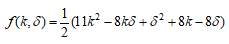 とおく時
とおく時
 …(B)
…(B)
の有理数解y>0,k, δについてy-f(k,δ)>0であればt>0となる。
同様に、y-f(k,-δ)>0であればt'>0となる。
よって、f(k,δ)<0かつf(k,-δ)<0となる(B) の解を見つければ、実2次体の5乗数の和であらわされる数が求まる(これは十分条件であって必要条件ではない)。
なお、 の条件は、
の条件は、 となる。
となる。
f(k,δ)<0かつf(k,-δ)<0となる範囲は下図の青色の部分である。

よって、(B) の解で、この範囲に入る(k,δ)を見つければ、実2次体の整数の5乗和で2通りに表わせる例が見つかる。
タクシー数 その8によれば、mを有理数として

であれば、(B) は(δ,y)に関する楕円曲線となり、有理点を探すことが容易になる。
-0.72<k<0となるmはおおよそ1<m<5もしくは-1<m<-0.2である。
ここで、mと-1/mに対するkの値は同一であることを考えれば、1<m<5の場合のみを考えればよい。
そこで、いくつかの1≦m<5について計算してみた。その結果が下表である。

* :(B) で定まる(δ,y)の4次楕円曲線をタクシー数その8の方法でWeierstrass標準形に変換したときにCoCalcで求めた無限位数の生成元の数
*2:*で説明したWeierstrass標準形の有理点群の無限位数の生成元
*3:左欄の生成元を1~7倍したときに、その数から元の4次楕円曲線の有理点(δ,y)を求め、t,t'のどちらかが正とならない場合を×、両方とも正であるが、f(k,δ)またはf(k,-δ)の双方は負ではない場合を●、双方とも負である場合○とし、左から右に結果を並べた。なお、7倍までで○が出ない場合は、より多く試したケースもある。
*4:この欄の値は近似値。kが水色の範囲に入るかどうか判断しやすくするために表示した。
このように幾つか試したケースでは、上図の水色の範囲に入るkの場合は必ず〇となる、つまりf(k,δ)<0かつf(k,-δ)<0となる有理数解が存在する。また、そうならなくとも、実2次体の整数の5乗和で2通りであらわせる、つまり●となる有理数解が数多く存在する。
一例として、m=4, k=-84/325のとき、有理点(70176/8125,5457408/528125)を選ぶと、上表で最初が〇である。この有理点より、δ=28/143が求まる。
これからs,s',t,t’を求め通分すると、

が得られる。
上記水色の範囲の有理数kを指定すれば、水色の範囲に入る(k,δ)が存在するか、つまり有理点を何倍かすればδの絶対値は十分小さくなるのだろうか。もし、そうであれば、実2次体整数の5乗和で2通りに表せる例が無限に存在しそうである。









