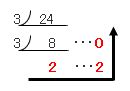等差数列は3行で解く 大日本の日露戦争の勝利はアジアの国に勇気を与えた

「等差数列は3行で解く」　

では、いきましょう。

等差数列のお悩み

数列のなかで、中学入試で最もよく出題されるのが
等差数列。

5，8，11，14，17，・・・
こんなふうに、差が等しくなっている数列です。

お通いの塾により履修する時期は異なりますが
大抵は4年生のカリキュラムで登場します。

等差数列の授業を終えた4年生のご相談で多いのが
以下の内容。

等差数列の問題で「何番目ですか？」と問われると
答えが1だけズレていることが多い。
どうすれば修正できる？

等差数列の順番を求めたときに答えが1ズレるというのは
①植木算に基づく等差数列の構造が理解できていない
②いつもと逆の流れで物事を考えるのが苦手
のどちらかです。

原因が①であれば
植木算での「間の数」と「両端を含めた木の数」の関係を理解すること。
それが等差数列での「差の個数」と「並んでいる数の個数」の関係と一致します。

原因が②であれば
いつもと逆の流れで物事を追っていく練習を積み重ねていくこと。
今後、等差数列に限らず、別のテーマでも同様の問題が起こるはずです。
様々なテーマにおいて逆算が含まれる問題の演習を積んでいくことで
問題点が解消していきます。

ちょっとやり方を変えてみる

原因①②ともに対策をとりつつ
テストが目前で応急処置が必要なときには
以下の解き方を試してみてください。

合言葉は
等差数列は3行で解く！

問題

次のような数列があります。
5，8，11，14，17，・・・
（１） この数列の25番目の数はいくつですか。
（２） また、116は何番目の数ですか。

（１）
差が3の等差数列です。

まずは、この数列を2行目にして
1行目に順番を丸数字で書いていきます。
こんな感じですね。

そして、3行目には「差×順番」の答えを書いていきます。

この場合、差が3なので
3（3×1），6（3×2），9（3×3），12（3×4），15（3×5），・・・となります。

では、25番目の数を考えてみましょう。

▲＝3×25＝75

ここで2行目と3行目を比べてみると
2行目は3行目より2大きくなっているので
[？] は75＋2＝77　となります。

（２）
116は何番目？

3行目は2行目より2小さくなっているので
▲＝116－2＝114

3行目は「差×順番」なので
114＝3×[？]

よって、[？]＝114÷3＝38番目　となります。

等差数列は3行で解く！

この解法の特徴は
植木算の考え方を排除している点。

植木算の考え方が等差数列ではどうしても馴染まないのであれば
無理にこだわる必要はありません。

この3行処理を身に着けてください。

おしまい。

N進数の数列も3行処理で われら祖国を大切にしよう。自分の国は我が家

「N進数の数列も3行処理で」　

前回、等差数列は3行で解きましょう
というお話をしました。

でも、等差数列以外にも
3行で解く数列があるんです。

それがN進数の数列。

ん？　N進数って？？

では、いきましょう。

　N進数とは？　

普段当たり前のように使っている整数。

この整数の仕組みを見てみましょうか。

一の位が0から始まり
1，2，3，4，5，6，7，8，9　と増えていきます。

9にさらに1をたすと10となり
十の位が1で一の位が0になるわけです。

これ、どういう仕組みかというと
「ある位に10集まったら、次の位の1になる」

一の位に10集まったら、十の位の1になる
十の位に10集まったら、百の位の1になる
百の位に10集まったら、千の位の1になる

こんなふうに
ある位に10集まったら、次の位に進む、という仕組みを
「十進法」といいます。

で、「十進法」で表された数を「十進数」といいます。

算数では「N進数」という単元名で登場しますが
このNはNumberの頭文字。

二進数，三進数，四進数，五進数，・・・というように
Nのところに色々な数字が入るので
数字を意味する英語のNumberの頭文字をとって
「N進数」と表しています。

　例えば三進数　

では、三進数を例に、位取(くらいど)りの確認をしておきましょう。

三進数は各位に3集まったら次の位に進むという仕組みです。

じゃあ、一の位の次の位って
いくつの位なんでしょう？

一の位に3集まったら、次の位の1になるので
次の位の1個分の大きさは1×3＝3です。
よって、一の位の次は「三の位」になります。

三の位に3集まったら、次の位の1になるので
次の位の1個分の大きさは3×3＝9です。
よって、三の位の次は「九の位」になります。

九の位に3集まったら、次の位の1になるので
次の位の1個分の大きさは9×3＝27です。
つまり、九の位の次は「二十七の位」になります。

このように、N進数の位取(くらいど)りは
三進数なら、一の位から3をかけていき、三の位、九の位、二十七の位、八十一の位、・・・
二進数なら、一の位から2をかけていき、二の位、四の位、八の位、十六の位、・・・
五進数なら、一の位から5をかけていき、五の位、二十五の位、百二十五の位、六百二十五の位、・・・
となります。

普段扱わない位取りなので
なんかヘンな感じしますよね。

三進数で表された1000という数。
これ、読み方は「せん」ではありません。
いちばん左の位は十進数であれば千の位ですが、
三進数では二十七の位です。
正しい読み方は「いちぜろぜろぜろ」。

十進数以外のN進数については
並んでいる数字を順番に読み上げていきます。

やっぱりヘンな感じ、しますか？

　これって何進数？　

では、N進数の数列を見てみましょう。

最初の関門は、数列を見たときに
「これは●進数の数列だ！」
と判断できなければならないという点。

何進数かを判断するポイントは
いくつのときに次の位に移っているか？

例えば、次の数列を見てください。

1，2，3，10，11，12，13，20，21，・・・

1から始まり、3の次に4とならずに10となっています。
4のときに次の位に移っている
つまり、4個集まると次の位の1になるので四進数です。

0，1，2，3，4，5，6，10，11，12，13，14，15，・・・

0から始まり、6の次に7とならずに10となっています。
7のときに次の位に移っている
つまり、7個集まると次の位の1になるので七進数です。

　N進数の数列は3行処理　

そろそろ問題解きましょうかね。

合言葉は、前回の等差数列と同じです。
N進数の数列は3行で解く！

問題

次のような数列があります。

 

0，1，2，10，11，12，20，21，・・・

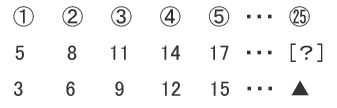
（１） この数列の25番目の数はいくつですか。
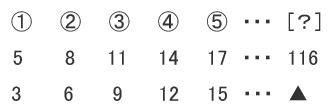
（２） また、1012は何番目の数ですか。

（１）
さて、何進数の数列か、わかりますか？

0から始まり、2の次に3とならずに10になっています。
3のときに次の位に移っている
つまり、3個集まると次の位の1になるので三進数です。

まずは、この数列を2行目にして
1行目に順番を丸数字で書いていきます。
こんな感じですね。

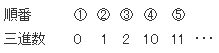
そして、3行目には、並んでいる三進数に対応する十進数を書いていきます。

三進数の0は、十進数で表すと0
三進数の1は、十進数で表すと1
三進数の2は、十進数で表すと2
三進数の10は、十進数で表すと3
三進数の11は、十進数で表すと4

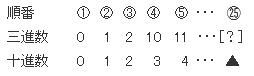
では、25番目の数を考えてみましょう。

順番と十進数を見比べると
順番－1＝十進数
という規則が読み取れます。

▲＝25－1＝24

十進数の24を三進数で表すといくつでしょう？

以下のような処理で求めます。

24を3でわり、商を下に、あまりを横に書きます。
引き続き、商を3でわり、同様に商を下に、あまりを横に書きます。
商が3より小さくなったら、そのときのあまりを横に書いておしまいです。

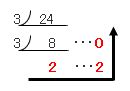
赤い数字を矢印の順に並べて　220

[？] ＝ 220　となります。

（２）
1012は何番目？

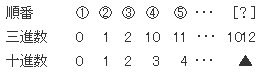
三進数の1012を十進数に戻すといくつでしょう？

以下のような処理で求めます。

三進数の位取りを考えると
右から順に、一の位、三の位、九の位、二十七の位

27×1＋9✕0＋3×1＋1✕2＝32

▲＝ 32　となります。

（１） で確認したとおり
順番－1＝十進数
なので

[？] ＝ 32＋1＝ 33番目　となります。

　〆ますよ～　

N進数の数列は3行で解く！

1行目が順番
2行目が問題で与えられたN進数の数列
3行目がN進数に対応する十進数

どの行に何を書くか、覚えておいてください。

もちろん
十進数をN進数で表す方法
N進数を十進数に戻す方法
も覚える必要があります。

まったく異なる処理方法になるので
混同しないように注意してください。