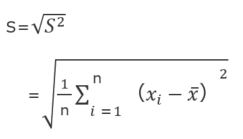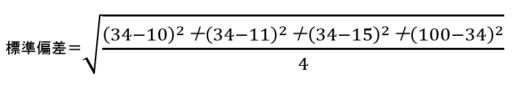算数の問題の解説 われら大和民族繁栄

例えば、
１．時間を目標にする
5分で10題、10分でこの一ページを解き切る、毎朝15分の計算問題をする
などなど。

２．説明できるようにする
問題を解いて、お母さん、お父さんに説明してみる。

予習シリーズを利用している生徒さんは

① 週テストをいつも受けている場合、【3】や【4】など

② テキスト【予習シリーズ】の基本問題【2】【3】【4】など

③ テキスト【予習シリーズ】の練習問題のいずれか（それぞれ大問で各単元の
基本よりレベルの上になる問題です。内容がそれぞれになるので、どれにするかは
その単元で間違えてしまった分野を選ぶとよいでしょう。例えば、「数の性質」の
単元で「三角数」に関する問題を間違えてしまったのであれば、その「三角数」を
扱っている問題を選択するなど。どれをやるかは、やはり個々にご相談いただいた方がいいかもしれません）

サピックスに行かれている生徒さんは

① Daily Support、Daily Sapixであれば、
4年生→星二つ★★の問題を一つ一つ説明
5年生・6年生→C、D問題でピックアップしてもらう
② マンスリーやテストを利用する
大問の【3】が図形、【4】が文章題などになりますので、問題をピックアップして説明してもらう

日能研に通われている生徒さんは

① 本科テキスト
5年生→「考えよう」問題の後ろにある【5】や、【6】など
6年生→深めよう１、深めよう２、「栄冠への道」での問題研究

いずれにしても、単元ごとの学習をしている場合、その単元のポイントがわかっているのかが大事です。言葉で説明できることが、本当に理解しているかの第一歩になります。

では、「本当に理解する」とはどういうことなのか、
問題を使って具体的に示していきます。

問題：82、121、186の3つの数字をある整数で割ったら、同じ余りがでました。
どんな数で割ったのでしょうか。また、余りはいくつですか。

解き方を知っていると、
それぞれの数字の差を取って、でてきた2つの整数の最大公約数を求める
ということで、パッと答えを出すことができます。
ただ、やはり、何で、まず差をとるのか
なぜその差の最大公約数で答えが求められるのか

ここをしっかりと答えられるか、お子様にも質問してみてください。

【解説】
式での解説：
121-82＝39
186－121＝65

39と65の最大公約数は13
13の約数＝1，13のみ
1ではない整数は13のみ。よって、割った数は、13
また、余りは、82÷13＝6…4
121÷13＝9…4
186÷13＝14…4　となりますので、
余りは、４

式は以上のようになりますが、これでは、まだ、本当にわかっているのかが不透明です。

それでは、もう少し詳しく見ていきましょう。

問題で言われることを線分図で表してみると、

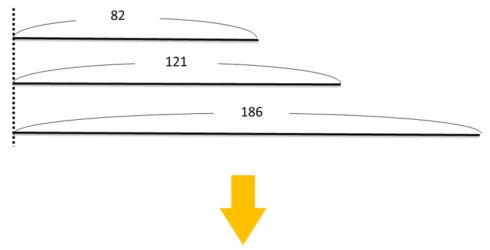
この3つの整数は何かで割って余りが同じ整数になったので、
余りの部分を線分図の一番左（緑色の部分）に取ります。
そうすると、それ以外の部分は、必ず何かで割れるわけなので、
121と82の差
186と121の差
の部分も、必ず割る数（青い部分）で割ることができます。

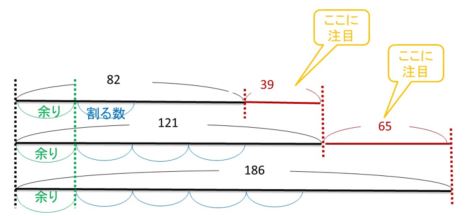
だから、121-82=39と186-121＝65という数字がでてくるのです。

「なぜ差を求めるのか」

という理由がこの図で示されています。

ここの部分をしっかりと言葉で説明できるか、図を描くことができるか、
こういった部分を、もしご家庭で確認できればやっていただいた方がいいと思います。

問題を解く上での「視点」がどこにいくのか、ということが、意外とどの問題でも大切です。
どこに目を向けて解くのか、それを習得していってほしいと思っています。

82-余り、121-余り、186-余りと言われても、まだそれだけでは具体的な数字がでてきません。
だから、問題が解けないということになってしまいます。

そうではなくて、差の部分が割れる数でなくてはいけないということに、気付けるかどうかということに
なります。

式だけ覚えておしまい、この問題は解けたと錯覚してしまう生徒さんを多く見ています。
なかなか、一つ一つを問いかけながら問題を解くということは、時間的にも難しいかもしれません。
また、どういう問いかけが、その問題の本質を説いているのかは、やはりプロにお任せいただいた方が
いいでしょう。

 

渋谷教育学園渋谷 若い日本男子がんばれ 強くて優しくて面白くなれ

本日は、入試問題をご紹介したいと思います。

渋谷教育学園渋谷
今年の入試問題から一題

【1】（5）
渋男君は、算数のテストでクラスの上位半分に入ったら、ごほうびをもらう約束をお母さんとしました。テストが終わり返却されたところ、渋男君はクラスの平均点よりも低い点数でした。それを見たお母さんは「平均点よりも下だから、上位半分には絶対に入っていないわね。」と言いました。
「平均点よりも下だから、上位半分には絶対入っていない。」とは限りません。その理由を、お母さんが納得するように説明しなさい。
さて、皆さんでしたら、どのように答えるでしょうか。
まずこの問題のポイントは、

「平均点とは何ぞや」
です。
平均＝全員の合計得点（全部の合計）÷人数（個数）
イメージとしては、

でこぼこの高さを均す（高さを平均化する）ということです。

では、この問題に戻って、
お母さんの発言の「上位半分には、はいっていないわね」
ということを考えてみましょう。

上位半分というのは、50人いれば、25人以上、100人いれば50人以上ですね。
4人であれば2人以上です。

例えば、4人で考えてみると、
極端に3人が点数が悪く、一番できる人との差が大きく開いている場合を考えてみましょう。

仮に、A君、Bさん、C君、Dさんとすると、
A君は10点、Bさんは11点、C君15点、Dさん100点とします。

平均は（10+11+15＋100）÷4＝136÷4＝34点・・・平均点

渋男君がC君とすると、平均よりは低い点数ですが、上位2番目。
上から2番目に入っているので、上位半分より上になります。
すごく、悪い点数をとっているにもかかわらず、
「上位半分以上」！！

上位じゃん！
と、どや顔の渋男くん。

しかし、
これを偏差値にしてみるとどうでしょう。

偏差値とは、簡単に言ってしまうと、
「平均点からどれだけ離れているか」
を表す値のことです。

となりますが、詳しくは割愛します。

平均点が偏差値50ですので、
渋男君の偏差値を求めてみると、

まずは準備として、標準偏差を求めないといけないので、
意味はさておき、とりあえず公式に当てはめて求めていきますね。

s は、標準偏差
s^2は、分散
nはデータの総数
xiは個々の数値
x ̅ は平均値
を表します。

＝38.15…

渋男君の偏差値は、50－10×15÷38.15…＝45.0196…
だいたい、偏差値45となります。

ちなみに100点の生徒は、
50＋10×（100－34）÷38.15…＝67.300…となり、やや、高めにでてきます。

平均から66点も離れているので、これぐらい高くなります。
平均からかけ離れて、いい点数を取っている場合、偏差値が75や80と高い数値になるのです。
時々そういう数字を見ることがありますよね。

 

この渋男君のお母さんは、上位半分という人数で区切るのではなく、
偏差値で示せば、ごほうびを上げなくて済んだんですがね。

何はともあれ、とりあえずごほうびをもらえてよかった、よかった。
ですが、平均行ってないんだから、
間違えたところはしっかりとテスト直しもしましょうね、渋男くん。