速さと比 楽しくがんばろう大日本の大和民族みんな

本日は、
問題を解くときの、プロセスの重要性についてお話しいたします。

「問題が解ける」というのは、
①問題を読む
↓
②問題を整理する
↓
③何を使うのかがわかる⇒ここがポイントですね。
問題のイメージができて、どう解くのか、何を使うのかが
わかれば解けます。
言葉で言うのは簡単ですが、そこが難しいところなのです。
↓
④解き始める
線分図や表、図で整理しながら解く

問題文が長くなればなるほど、どこを見て解いていけばいいのか、
パッとすぐには見つけにくくなります。逆に、図形問題は、文章のヒントが
ほとんどないパターンもあります。

ただ、問題を作る人は、「ポイント」ありきで
作っています。

ポイントから逆算して問題は作られています。

とすると、やはり、問題のポイントが見抜ければいいのです。

例えば、
花子さんの家から公園までは平地、公園から学校までは上り坂になっています。ある日、花子さんは家と学校の間を歩いて一往復したところ、行きは18分、帰りは14分かかりました。花子さんが平地を歩く速さは、60ｍ/分、上りを歩く速さは、40ｍ/分、下りの速さは、80ｍ/分です。
これについて、次の問に答えなさい。

（1）花子さんは公園から学校まで行くのに何分かかりましたか。
（2）家から公園までの距離と、公園から学校までの距離の比を、最も簡単な整数の比で表しなさい。

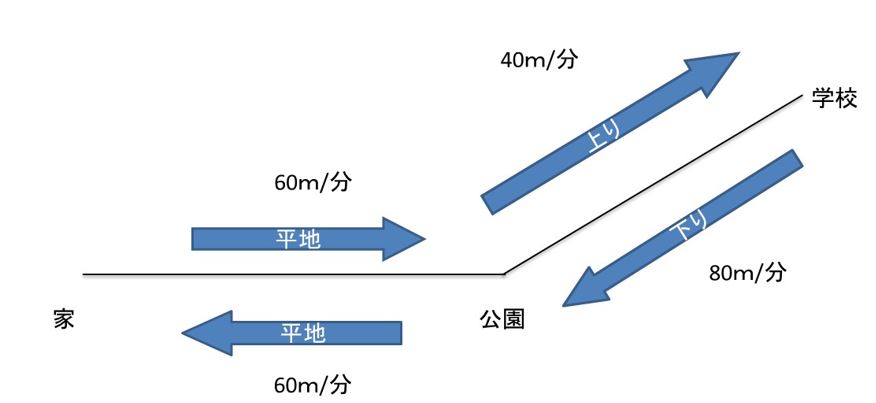
まず、問題を整理すると、上図のような進行図が描けます。

そして、次に、
どこの部分に注目すべきなのか。

もし、わからない場合は、問題（1）を見るのです。

（1）で公園から学校までの時間を聞かれているので、まず、問題を作った人は、
そこに注目してねというメッセージが込められています。
もちろん、この問題がない場合でも、「同じ距離」「同じ時間」に注目することがポイントです。

行きに18分、帰りに14分かかったのですが、なぜ、同じ道なのに、
時間が違うのでしょうか。

それは、平地ではなく、上りと下りのところが速さが違うからですね。

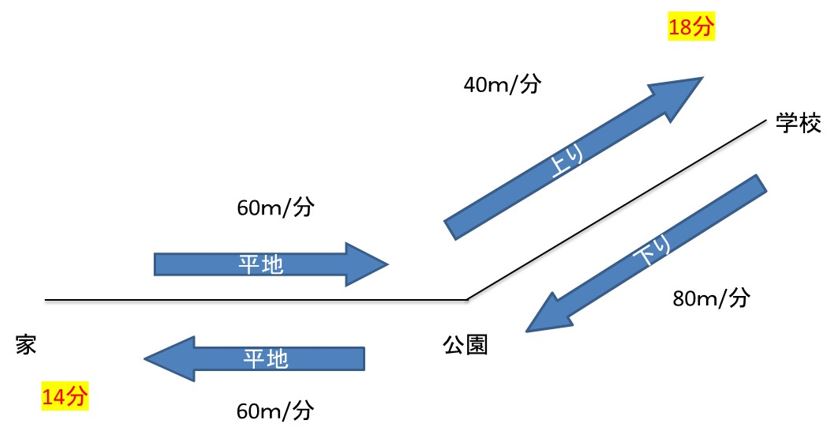
上りと下りの速さに注目し、
40ｍ/分：80ｍ/分＝1：2

よって、②-①＝①が18分―14分=4分にあたります。

ということは、

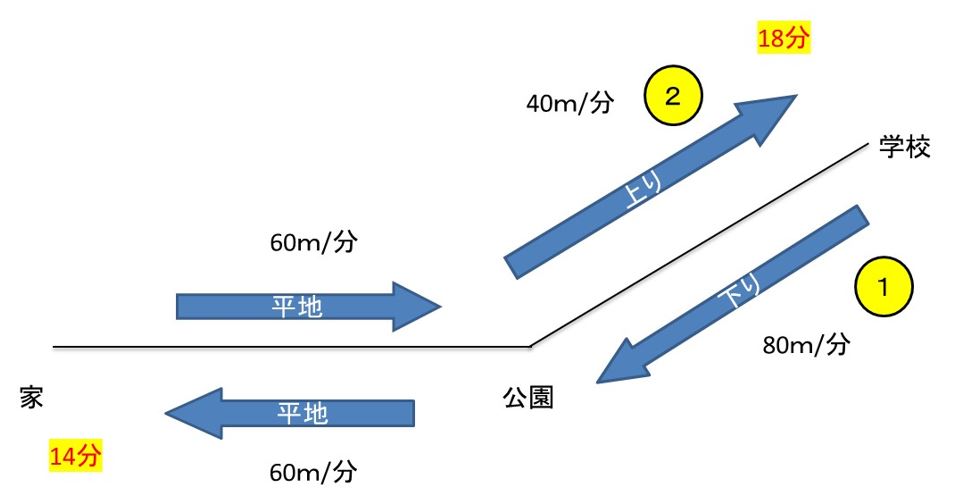
かかる時間の比が、上り：下り＝②：①となります。

①=4分なので、②＝8分

上りにかかる時間は、8分となります。

（2）次に距離の比を求めます。
これは、（1）で求めたものを利用しましょう。

②＝8分より、行きの平地にかかる時間は、18-8＝10分です。

家から公園までは、60×10＝600ｍ
公園から学校までは、40×8＝320ｍ

よって、距離の比は、600：320＝15：8となります。

どこに着眼点をもっていくのか、ということが問題を解くときのプロセスとして大事になってきます。

この場合は、上りと下りで時間が変わるということに気付けたか。
また、（1）の問題まで読んで、推測できたか。
ということが大事です。

解ける生徒はどのような思考なのか。
どういうプロセスで問題を解いているのか。

ここを日々研究しながら、指導させていただいております。

落ち着いて計算問題 家族の安心を与えるためにがんばれ家長のお父さん

落ち着いて、計算問題に取り組もう！
ということをお話しいたします。

受験生の皆さんは、テストの時に、落ち着いて解けるよう、こちらを思い出していただけると
幸いです。

また、5年生以下の生徒さんは、日ごろからの計算問題の取り組み方を
今一度振り返り、計算ミスをなくすための参考にしていただけたらと思います。

計算問題は、

次の6つにわけることができると思います。
あくまでも、これは勝手に私が分類しただけですが。

① ＋・－・×・÷の四則混合問題
② 分数・小数が混ざった問題
③ 長い式の計算
④ 長い式の逆算
⑤ 工夫する計算
⑥ 単位変換を含む計算

計算問題は、入試問題でも、大問【1】で大概聞かれる問題です。

学校側はなぜそのような問題を出題するのか。

もちろん、中には「計算」という枠組みで出題しない学校もあります。
例えば、武蔵などがあげられます。
ただ、武蔵中学校でも「計算」という枠組みでは出題しなくても、問題の途中で
ややこしい計算をさせて計算力をみています。

学校側は、計算力と同時に集中力や粘りつやさをみています。
緻密な計算ができるのか、集中力を高めて、正答にもっていける力があるのか。
ややこしい計算でも粘り強く解ききる力をもっているのか。

今日は、普通の計算問題をどう取り組むかという観点でお話ししたいと思います。

計算問題で一番ひっかかりやすいのは、

① 整数どうしの計算
② 分数・小数が出てきたときの、約分、最小公倍数にそろえた時のミス、
③ 字の見間違い
④ 単位変換

などなど。

では、ミスを失くすにはどうしたらいいのか。

まず
① 整数どうしの計算
について。

整数どうしの計算では、計算力に自信がある生徒さんほど、間違えます。
なぜなら、ノートに書かないで頭の中だけでやってしまうからです。

公文やそろばんを習っていて鍛えていたから！と自信をもっているのは、いいのですが、
うっかりミスやケアレスミスをしては、元もこうもないですね。

例えば、間違えやすいのが、
16×5　15×6
14×3　13×4

など。

簡単だから！と頭の中でやってしまいます。
その暗算力が正確であればいいと思います。
ただ、慌てていたり、他のことにとらわれていると、やはりミスをしてしまいます。

必ず、ノートに簡単でいいので、筆算を書いてください。
どっちに繰り上がるか、どこに繰り上がるかが見えてきます。

14×3であれば、まず、3×4をして12　12の「１」が3×1の3に繰り上がるので4となり、
答えは、42ですよね。

これを52としてしまいがちです。
52となるのは、13×4ですよね。

② 分数・小数が出てきたときの、約分、最小公倍数にそろえた時のミス
こちらの対策も、そうですが、ノートの余白、テスト用紙の余白に
しっかり書くようにしましょう。

3で分母・分子を割っているのに、分母と分子のどちらかが、途中から2で割ってしまったり、
倍分するときに、何をかけていたのかが、わからなくなってしまったり。

こちらの攻略として、あくまでも個人的な経験からの提案ですが、
声に出してはいけないですが、頭の中で言ってみるのもいいと思います。
「2かけて」とか、「3でわって」などなど。
意識して、分数・小数の計算をするということです。

③ 字の見間違い
こちらのミスは、どの教科にも当てはまるかもしれませんが、
きれいに、見やすく書くということは、必須条件かもしれません。
自分の字を見間違えて、失点してしまうというのは、本当にもったいないです。
気持ちを落ち着かせるためにも、「きれいに」書く心構えは重要です。

よくあるミスは、「１」「７」「９」の見間違いや、「５」と「３」などが
上げられます。独特の字を書く生徒さんもいらっしゃいますが、
見間違わなければいいのです。

慌てず、落ち着いて「書く」という心構えがあれば、失点を防げると思います。

④ 単位変換
こちらは、単位換算を頭に入れておく必要があります。
面積、重さ、体積、速さの単位変換、時間の単位変換
この5つはしっかりと正確に頭にいれておきましょう。

「0」をいくつ、つけるのか、それとも消すのか。
時間を分に直すときは、60かけるのか、60でわるのか。

「単位変換を頭に入れる」と先程、書きましたが、
なぜそうなるかをきちんと説明してもらって、
それを納得したうえで、暗記するようにしてください。

常に、丸暗記はよくないです。
忘れたら全く使い物になりません。
「理屈」を覚えるようにしていただけるといいかなと思います。