図を描く～〇描いて みんなで大きい和 それが大和

問題を解くときに、「手をうごかして」「とにかく描く」といわれることが
多いのではないでしょうか。
しかし、どのように描くのか。問題集やテキストの解説には完成図は描かれているのですが、
実際どこから描くのか、それを示してくれていません。

そこで、本日は、描く手順を示していきます。

次の図を見てください。

この図って、「水量とグラフ」の単元を勉強するときによく見る図ですよね。

この図ってどこから描くのでしょうか。
授業をやっていても、話しながら、少しずつ問題を紐解きながら
解いていくのですが、「じゃ、描いてみて」と言ってやらせてみると、
ただ、なぞって上のほうからL字型にいきなり描いたりします。

そうではなく、
描く順番があるのです。

お絵描き歌というのを小さいころやったことがあると思います。
ドラえもんを描くときも、「♪〇描いてチョン、〇描いてチョン♪」
とリズムと歌に合わせて描いたと思います。

それです！！
まず描く順番があります。
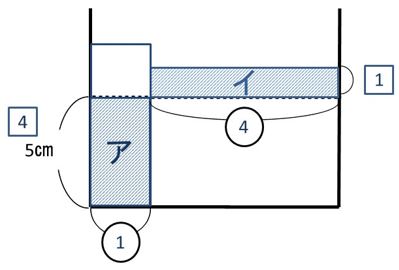
【問題】
底面積が500㎠で、深さ20㎝の直方体の形をした水そうと、一辺10㎝の立方体のおもりがあります。
いま、水そうに6㎝まで水をいれました。
立方体のおもりを1つ入れると水の深さは何㎝になりますか。

まず、
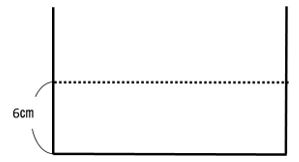
手順①水そうを描きます。

手順②入っている水の深さ5㎝という横棒を入れます。

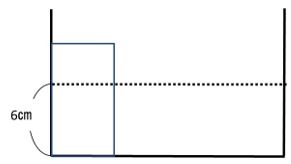
手順③おもりを沈めます。

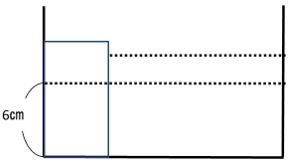
手順④おもりを入れた後の水の深さを表す横線をいれます。

手順⑤上がった分₍イ₎とおもりが入る前にあった水（ア）の部分が等しいという図をいれます。

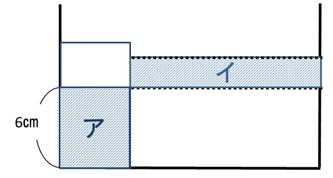
手順⑥底面積の比を求めます。

ここが解くポイントになります。『イメージde暗記　根本原理ポイント365』の基本編070、実践編163にありますのでお持ちの方はチェックしてみてください。
底面積比がア：イ＝100㎠：（500－100）＝1：4となります。
アとイの面積が等しいので、ア：イの横の比が1：4となり、たての比は4：1と逆比が成り立ちます。
そうすると、下の図ができあがります。

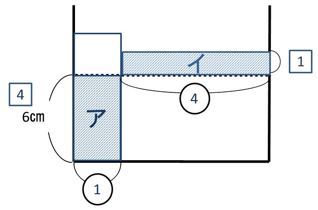
4⃣＝6㎝
1⃣＝1.5㎝になります。

水の深さは、6＋1.5＝7.5㎝と求めることができます。

いかがでしょうか。
自分1人で描けるかどうかやってみてください。

授業の中では、横にいて描いている過程を見せます。
それをまねして家でやってきてほしいと思っています。

この単元だけではなく、どの単元もイメージ図が大事です。
描き方を示し、まねして、練習するというサイクルを作っていきます。

ひとひねり問題～角度編～ がんばろう日本男子 わが国も大和撫子も日本男子が守る

「算数の問題が解ける」ということは、
① あることに気が付いて
② 式を計算することができて
③ 答えが出る

このスリーステップを踏んでいるのではないでしょうか。

この①の「あることに気が付いて」
という部分が、ぱっとわかる問題か、手を動かして何かを書き出して気づける問題と、
またその中間の問題があると思われます。

ぱっとわかる問題というのは、5年生の前半で終わると考えてください。
5年生の前半までで、算数の気づかなくてはいけないポイントを
教えてもらっているということになります。その気づかなくてはいけないポイント
というのは、今後の5年生後半、6年生、入試に続く重要なポイントとなります。

重要ポイントは、
『イメージde暗記　根本原理ポイント365』の基本編100、実践編265にあります。
ちょっと宣伝が入ってしまいましたが。

それでは、そのポイントをどう使って、どう解くのかを例を使って示していきます。

こちらの角度の問題はどうでしょうか。
問題：角アは何度か求めなさい。

これは練習を積んでいる皆さんは、
○○＋✖✖を求めて、〇＋✖にもっていけばいいと気づくと思います。（気づいてほしいです）
〇〇+✖✖＝180－58＝122
〇+✖＝122÷2＝61°
ア＝180－61＝119°

では、ひとひねりされているとどうでしょうか。

問題：　右の図の三角形ＡＢＣで、角Ａは66°、ＢＤ＝ＢＥ、　ＣＥ＝ＣＦ
です。このとき、角アの大きさを求めなさい。

二等辺三角形なので、底角が等しいというのは知っていますよね。
ステップ①
同じ角度には同じマークをつけましょう。

同じ辺にはチョンチョンマーク。
同じ角度には、〇や✖で同じマークをつけましょう。

そして
アを求めるためには、〇＋✖がわかればいいということまで来ました。

では？？

次に66°をどのように使うかです。
よく授業中も言うのですが、
算数の問題ででてきた数値というのは使わないということはほぼないと考えてください。
問題の中の情報はすべて使うという意識で問題を解くのもポイントの一つとなります。

66°は三角形の内角なので、
他の2つの角度の和は、180－66＝114°

あと少しです！！

ということは、
〇〇＋✖✖は2つの三角形に入っている角度なので、
180×2＝360°

360°-（イ＋ウ）＝360°－114°＝246°
○○＋✖✖＝246°
〇＋✖＝246÷2＝123°

よって、
ア＝180°－（〇＋✖）＝180°-123°＝57°
となります。

まとめると、

角度の問題で気づかなくてはいけないポイントは、
① 二等辺三角形、正三角形を探す
→角度がわかる図形があれば簡単！
② 同じ角度、同じ辺には同じマークをつける
→二等辺三角形、正三角形を探すため
③ いったん〇と✖など記号でおいてみる
→答えは出ないが、使えないかと疑う
この3つです。

そして、この問題のひとひねりは、
〇+✖が一回では求められないということです。

ぱっとみてわかる問題ではない時に
考えなくてはいけないことは、やはり気づかなくてはいけないポイントをまずは頭に
入れているかということです。ここは、本当に基本中の基本で、根本原理となります。
つまり、とっても大事なところということです。

そして、それを頭にいれながら、
どれが使えるのかなと考えながら手を動かし（ここではちょんちょんマークをつけるとか）、
自分で気づけるようにしていくということです。