算数の図はなるべく正確な図を描く 我らの祖国大和をもう一度繁栄目指す

本日は、図の描き方についてお話しいたします。

まず、ある生徒さんの描いた図をいくつか挙げてみます。
【例１】

【例２】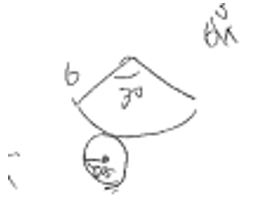

これは、母線6㎝、底面の半径0.5㎝である円すいの側面積を問う問題
に対して、それぞれの生徒さんが描いた図です。

ということで、側面の展開図を描いてますね。
うん、うん、できているよ。
そう、扇形の中心角は、より360÷12＝30°
ちゃんと、図にも30°を描きいれてますね。

6×6×3.14×＝9.42㎠
正解。
側面の面積を求めることはちゃんとできています。
が、しかし！！

次に「ひもと底面の円周との間にある、側面の斜線部分の面積を求めなさい」
という問題。さぁ、どうしましょう。

「30°ときたら？」⇒「三角定規の2辺比　１：２」だよねという
問答をいつも授業でやっているので、気付けていることを願う。

30°も描けているし・・・？？

しかしながら、
「30°」はかけていたのですが、30°っぽくないので、
30°60°90°の三角定規を見つけることができませんでした。

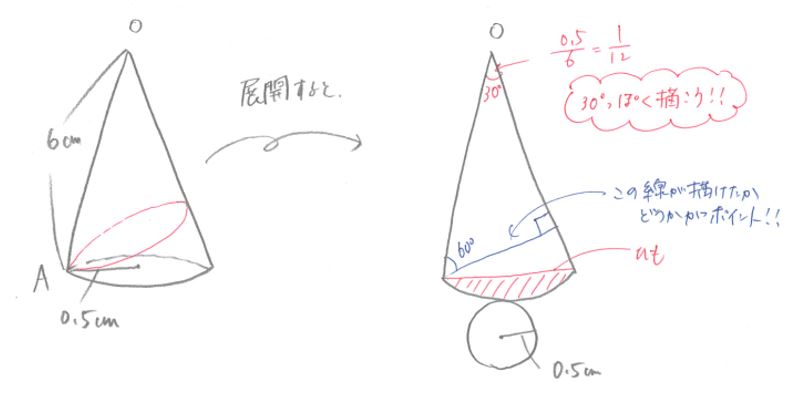
この青い線が引けたかどうかが、この問題を解けたかどうかの分かれ道です。

始めに載せた【例1】の図では、底辺と高さの直角の線を
描きいれていますが、やはり30°が60°っぽくなってしまっているので、
高さが何㎝なのかを見つけることができませんでした。
なんとなく、30°60°90°を見つけるんだろうなぁ、というところまでは行っているのに、
図が正確でないので、解き切れていないのです。もったいないです。

また、【例2】の図も、30°が120°くらいに開いてしまっていて、
この後の手だてが見つからずに終わっています。

「いいところまで行っているのに、もったいない」

何度言われていることか。本当につらいところだと思います。

これを、
「ちゃんと気付けたね！」
で終わらせるためにも、
図はなるべく正確に描けるようにしておきましょう。

この問題の正解は、
扇形から三角形を引いた面積となります。

三角形の面積は、底辺が6㎝、高さが１：２の関係より、１：２＝□：６㎝
□＝3㎝より、
6×3÷2＝9㎠
先程求めた扇形の面積、9.42㎠から、三角形の面積9㎠を引いて、

9.42－9＝0.42㎠
です。

今日お伝えしたいのは、
図を正確に描けるようにしておくことがいかに大事かということです。

例えば、基本図形の「正三角形」「正方形」「長方形」
また、「正六角形」「正五角形」くらいまで、なるべくきれいに描けるようにしておきましょう。
図が描ける生徒さんは、やはり図形問題が得意です。

図形の単元を勉強しているときは、問題を必ずノートに写して
解いてみましょう。
簡単な図形問題から「描ける」ようにしておくことが、図形問題の攻略に繋がります。
なぜなら、「描く」ときに、どうやって描こうかなと考えるからです。
そうすると、「あ、こことここの長さが等しいんだ」とか、
「角度が同じなんだ」ということが、見えてくるのです。
図形だけ与えられて、じーっと見ていても、意外とみているようで見ていない。
つまり、気付くべきところに気付けていないということがおこります。

まずは手始めに、
今日お子様が学校から帰ってきたら、
「正三角形って描ける？」「正方形ってどうなっているのかな」
と、描けるかどうか確認しながら、図形の特徴を言わせてみください。
「正三角形」であれば、角度がすべて60°で、辺の長さが全部同じ。など、
そういった答えが出れば○です。

また、
「30°ってどれくらい？」
などなど。

一緒にお絵かきしながら、図形の特徴をつかむ一言を添えてあげるといいと思います。

7つの計算力 お父さん家長と長男は跡継ぎ 男は強く優しく女を守る

計算でなかなか完答することができないというお悩みが
多いので、今日は計算についてお話したいと思います。

「計算」を分解すると、ざっと7つにわけることができるのではないかと思います。

① 四則計算ができているか
② 分数・小数の変換ができているか
③ まとめて計算する方法を知っているか
④ キリの良い数値を作るということを知っているか
⑤ 部分分数分解を知っているか
⑥ 単位変換を正確に暗記しているか
⑦ 約束記号のある計算を知っているか

お子様は、どの段階まで知っていて、どの部分でミスをしてしまっているのかチェックしてみてください。

以上に挙げた7つを更に一つ一つもっと細分化することができますが、
今回最もお伝えしたいのは、テストの時に計算で完答できるようにするということです。

計算ミスをしてしまっている原因は、
１． 字が雑かまたは大きすぎる
２． 頭の中だけで計算してしまっている
３． 上記の②-④が疎か（①はできるという前提で）

ということが挙げられるのではないでしょうか。

まず、
１.字が雑かまたは大きすぎる場合
日頃の勉強するノートに線を引いて、この場所にしか書けないというスペースを
作ってあげることが有効です。
とにかく、書くところがいっぱいあると生徒さんはめいっぱい書いてしまいます。
これがまだ低学年の時はオッケーです。書かないより書いて目で見える方がよいので。
ただ、5年生，6年生のテストにだいぶ慣れてきた生徒さんであれば、やはり「限られたスペースに書く」といことも意識していきましょう。
それに反して、きれいすぎるノートも要注意です。
きれいに書くことだけに注意がいってしまい、「限られた時間」ということを忘れがちです。
「限られたスペース」と「限られた時間」という2つがテストでは求められるということです。

2．頭の中だけで計算してしまっている場合
もちろん、暗記するべき数値もあるので、頭の中だけで使っているということはよいのですが、
いったんその暗記で出した数値を紙に書いておくということが大事です。
計算で難しいというのは、式が長くなる場合が考えられます。
一度にすべての操作を一気にやろうとすると、どこかでミスや勘違いをしてしまいます。

3．②-④を疎かにしている場合
②分数・小数の変換ができているか
③まとめて計算する方法を知っているか
④キリの良い数値を作るということを知っているか

分数から小数への変換、また、小数から分数への変換は必須です。
例えば、3.75や、0.625
などわざわざ100分の○○などのように、変換して約分してという作業をしていないかどうか。
また、
3.14や似ている数値がでてきたらまとめて1回の計算で終わらせているか。
99+999+9999という計算を、99に1を足せば100になるので、
100+1000+10000としてから3を引くというやり方をしていますでしょうか。

補足として、
⑤ 部分分数分解を知っているか
⑥ 単位変換を暗記しているか
⑦ 約束記号のある計算を知っているか

知っていても正確に使えないと意味がないです。
使えるようにするための練習が必要です。

それぞれの段階でミスをしてしまっている原因があると思います。それをお一人お一人の状況に合わせて指導させていたただきます。

ノートの書き方などは、一番有効なのは、友達がどうやって書いているのかを見るのが一番です。または、なかなか見せてもらえないかもしれませんが、テストの問題用紙を見せてもらうことです。
算数が得意だという友達のノートを一つ見せてもらって、そこで刺激を受けて、やっと自分の間違いに気づいた生徒さんもいらっしゃいます。