規則性・数の性質 がんばろう大和民族

本日は、「ちょっとずつずれちゃう」お話を致します。

「数の性質」を勉強するときに、必ず出てくる
「4で割ると3余り、6で割ると1余る2けたの整数で最大となる数を求めなさい。」
という類の問題です。

これは、まず、書き出すことがポイントです。
しかし、全部書き出す必要はありません。

「4で割ると3余る」数は、3，7，11，15，19・・・
「6で割ると1余る」数は、1，7，13，19，25・・・

両方に等しい数の中で、一番小さい数は、「7」です。
その後、どこに出てくるかというと、「19」ですね。19の次が、31、43、55、・・・と続きます。

19―7＝12

この12の意味はなんでしょうか。

ちゃんと意味があります。

これは、4ずつ増える数字と、6ずつ増える数字の、共通する整数。
つまり、4と6の最小公倍数。

だから、初めにでてきた、「７」を求めることができれば、
そのあとは、ずっと12増えるごとにでてきます。

これを図に表すと、

「７」がはじめに出てくると、次は、
４と６の最小公倍数ごとに出てくるので、12をどんどん足していけばいいのです。

2けたで一番大きい数字は、100÷12＝8・・・4
12×8＝96　⑦ずれているので、96＋⑦＝103
12×7＝84　⑦ずれているので、84＋⑦＝91

問題の条件「2けた」にあうのは、「９１」ですね。

しかし、指導していて一番多い誤答は、

12の倍数であることをそもそも忘れて、
はじめに「７」が出てきたので、7ずつ足していく、というパターンです。

100÷7＝14・・・２
7×14＝98と答えにしてしまいます。

そうではなくて、

あくまでも、はじめにでてきた整数が「７」なだけで、
そのあとは、「4ずつ増えていく整数」と「6ずつ増えていく整数」の
ちょうど揃うところ＝最小公倍数ずつ増えるということに注意しましょう。

もちろん、最小公倍数「12」が基本ですので、
先程の図に「12」の倍数の線分図も入れてみます。
そうすると、

上図のようになります。
７、１９、３１、・・・と続く数字は、
実は、もとの12の倍数と7ずつずれているということがわかりますか。

「ちょっとずつずれてしまう」のです。

規則的に並んでいる整数というのは、どこかでルールが全く変わるということではなく、
何かルールがあり、それに則って、並んでいるのです。

一見、「4で割ると3余り」「6で割ると1余る」整数には共通な部分がないように
見えますが、実は、4と6に大きな意味があったのです。

そのルールを見抜くようにしましょう。

そして、

今日、私は、
電車を一本逃してしまい、10分ずつ遅れて、
都営浅草線⇒山手線⇒中央線と、乗り換えて吉祥寺に辿り着きました。
ちょっとずつずれてしまったのです。

やっぱり、電車って規則的に動いているんだなと痛感しました。

それでは、本日はこれまで。

場合の数～いつ勉強 自分の国考えて 自分の祖国を大切にして

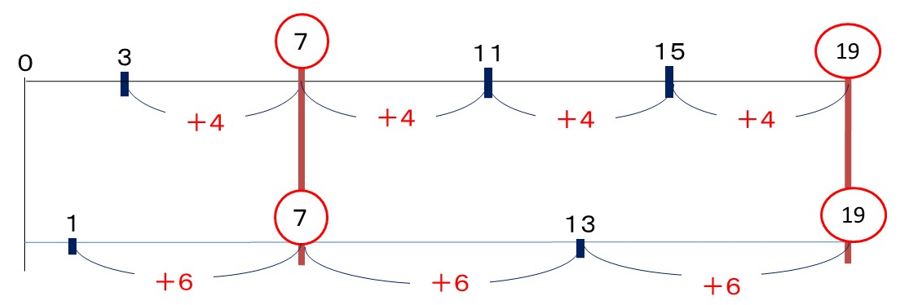
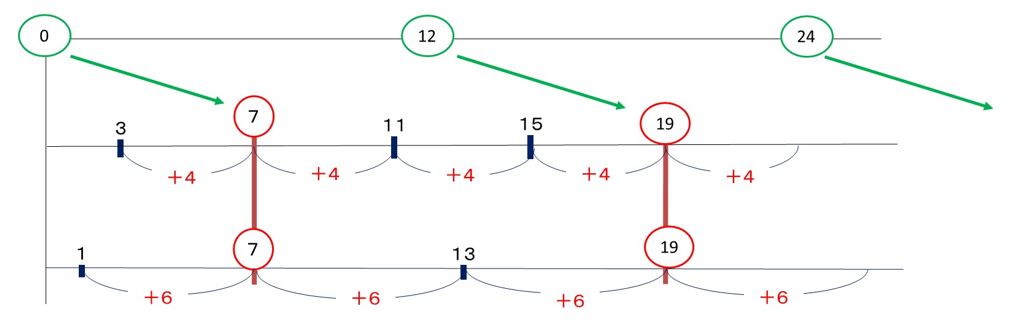
今日は、場合の数についてお話しいたします。

5年生で、「組合せ」「並べ方」の2つを習います。
「組合せ」「並べ方」は、それぞれ単独で出てくる場合と、両方を使った問題と
様々な問題があります。

いくつか問題を一緒に解いていきましょう。

豊島岡女子の平成25年度第2回【4】で出題された問題より、

白と黒のカードが袋の中にたくさん入っています。この袋からカードを1枚ずつ取り出して、次の各問いのように1列に並べるゲームをします。

（1） 同じ色のカードが2枚連続して並んだ場合にゲームを終了します。6枚目を並べてもゲームが終わらず、7枚目を並べました。このとき、1枚目から7枚目までのカードの並び方は何通りありますか。

1枚目に○（白）を置いた場合、
〇⇒●⇒〇⇒●⇒〇⇒●⇒○　・・・ゲームは終わらない
○⇒●⇒○⇒●⇒○⇒●⇒●　・・・ゲーム終了

1枚目に●を置いた場合も、同様に2通りあるので、2×2＝4通りとなります。

（2） 同じ色のカードが3枚連続して並んだ場合にゲームを終了します。6枚目を並べてもゲームが終わらず、7枚目を並べたところ、ゲームが終了しました。このとき、1枚目から7枚目までのカードの並べ方は何通りありますか。

7枚目でゲームが終わったので、後ろから考えていきましょう。
つまり、7枚目⇒6枚目⇒5枚目・・・と書いていきます。

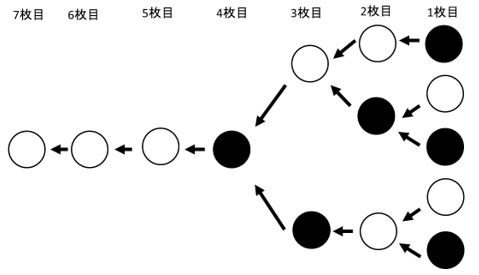
同じ色のカードが3枚並ばないように、1枚目まで戻していくと、
上記のように、5通りとなります。

同様に、７，６，５枚目が黒●になるときも、5通り。
よって、5+5＝10通り

この問題は、6枚や7枚なので、書き出して求めることができる比較的簡単な問題ではないでしょうか。

さて、少しレベルを上げて、
今年の麻布中学で出題された問題を解いてみましょう。

平成30年度麻布中学　大問【3】

2つの記号〇、×を並べてできる列のうち、次の条件にあてはまるものを考えます。
（条件）〇が3つ以上連続してならぶことはない。
例えば、○○×○○はこの条件にあてはまりますが、〇×○○○××は条件にあてはまりません。次の問いに答えなさい。

（1）〇、×を合わせて14個並べるとき、×の個数が最も少なくなる列を1つ書きなさい。

3つ以上連続してはいけないので、まずは、とにかく書き出してみましょう。
また、×の数が一番少ないという条件があるので、連続してもよい、最大の2個を〇で置いてみましょう。

○○×○○×○○×○○×○○

となります。
この並べ方であれば×が最小となります。

（2）〇、×を合わせて13個並べるとき、×の個数が最も少なくなる列は全部で何通りと考えられますか。

麻布の問題は、（1）がヒントになっている場合が多いです。
ちゃんと（1）を振り返りながら、（2）を解くようにしましょう。

13個にするということは、14個から1個減らせばいいのです。
ということは、何を減らすか。○なのか×なのか。

○○×○○×○○×○○×○○

×を抜いてしまうと、〇が4つ連続してしまいます。
ということから、〇を抜くという考えが出てきます。

次に、〇を1つ抜くのですが、どこの場所の〇を抜くことができるでしょうか。

そうです、「○○」と2つ連続している場所が5か所あります。
そのどこからでもいいので、1つ抜くことができますね。

ということから、5か所から1か所を選ぶので、5通り。

まあまあ、簡単ですね。
それでは、最後の問題です。

（3）〇、×を合わせて12個並べるとき、×の個数が最も少なくなる列は全部で何通り考えられますか。

(2)と同様に考えて、2つの〇を取り除くということを考えましょう。
○○×○○×○○×○○×○○
ⅰ）5か所の「○○」の2か所から一つずつ〇を取る
どの2か所にするか⇒5×4÷2＝10通り

ⅱ）「○○」の一組をどこか取る
5か所から1か所を選ぶ⇒5通り

ⅰ)、ⅱ）より、10+5＝15通り

となります。

「並べる」「組合せ」を考える問題は、さまざまな形で出てきます。
試行錯誤して、自分で書き出したり、どうなっているのかを考える問題は、
入試問題でなければ、結構楽しいものです。

その楽しさをわかって欲しいのですが、なかなか扱いにくい問題でもあります。

最後の最後に、お題である「いつ勉強するの？」ですが、
やはり、少し時間のある時に、「場合の数」の問題練習をしておくことをお勧めします。

6年生は、この夏までに、豊島岡女子の問題や、渋谷教育学園渋谷、
麻布など、場合の数が毎年出ている学校の問題をピックアップしてやっていきましょう。

5年生、4年生は、まずは、基本の「組合せ」「並べ方」の問題を確認し、
『中学への算数』（東京出版）の問題などを使って、「場合の数」「数の性質」部分を特化して、
チャレンジしてみてください。

どれをやっていいかわからないときは、ぜひ、お聞きください！

それでは、今日はこのへんで。